1 chiếc lều trại có dạng là hình chóp tứ giác đều có các kích thước như hình vẽ bên . Hãy tính diện tích vải lều cần để phủ kín các mặt bên của lều (ko tính mép dán) biết rằng chiều cao kẻ từ đỉnh của mặt bên là 3,2m 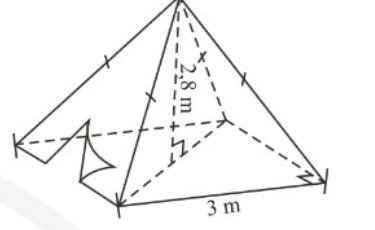

Những câu hỏi liên quan
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.a) Tính thể tích không khí trong chiếc lều.b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là 3,18m và lều này không có đáy.
Đọc tiếp
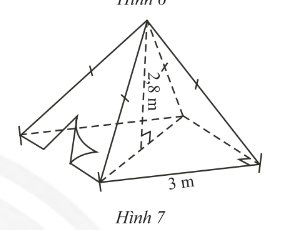
Một chiếc lều có dạng hình chóp tứ giác đều ở trại hè của học sinh có kích thước như Hình 7.
a) Tính thể tích không khí trong chiếc lều.
b) Tính diện tích vải lều (không tính các mép dán), biết chiều cao của mặt bên xuất phát từ đỉnh của chiếc lều là \(3,18\)m và lều này không có đáy.
a) Thể tích không khí trong chiếc lều là: \(\frac{1}{3}{.3^2}.2,8 = 8,4\) (\({m^3}\))
b) Độ dài trung đoạn của hình chóp là: \(\sqrt {2,{8^2} + 1,{5^2}} \approx 3,18\)
Diện tích vải lều là: \(\frac{{4.3}}{2}.3,18= 19,08\) (\(c{m^2}\))
Đúng 0
Bình luận (0)
Bài 2: Một túp lều có dạng hình chóp tứ giác đều, có kích thước như hình bên a) Tính thể tích không khí bên trong chiếc lều. b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết trung đoạn của hình chóp là 3,18m và giá vải là 15.000 đồng/m2 . Ngoài ra, nếu mua vải với hóa đơn trên 20 m2 thì được giảm giá 5% trên tổng hóa đơn.hình chiếc lều vừa chụp trong bài vừa nãy và đây là đề bài.Bài 3: Người ta thiết kế chậu trồng cây có dạng hình chóp tam...
Đọc tiếp
Bài 2: Một túp lều có dạng hình chóp tứ giác đều, có kích thước như hình bên a) Tính thể tích không khí bên trong chiếc lều. b) Tính số tiền mua vải phủ bốn phía và trải nền đất cho chiếc lều (coi các mép nối không đáng kể). Biết trung đoạn của hình chóp là 3,18m và giá vải là 15.000 đồng/m2 . Ngoài ra, nếu mua vải với hóa đơn trên 20 m2 thì được giảm giá 5% trên tổng hóa đơn.
hình chiếc lều vừa chụp trong bài vừa nãy và đây là đề bài.Bài 3: Người ta thiết kế chậu trồng cây có dạng hình chóp tam giác đều, biết: cạnh đáy khoảng 20cm, chiều cao khoảng 35cm, độ dài trung đoạn khoảng 21cm. a) Người ta muốn sơn các bề mặt xung quanh chậu. Hỏi diện tích bề mặt cần sơn là bao nhiêu? b) Tính thể tích của chậu trồng cây đó (làm tròn kết quả đến hàng phần trăm). Biết đường cao của mặt đáy hình chóp là 17cm.Bài 6: Cho tam giác ABC cân tại A, đường trung tuyến AM. Gọi I là trung điểm của AC và K là điểm đối xứng với M qua điểm I. a) Cho AB = AC = 10cm; BC = 12cm. Tính AM? b) Tứ giác AKCM là hình gì? Vì sao? c) Chứng minh: AKMB là hình bình hành. d) Tìm điều kiện của tam giác ABC để tứ giác AKCM là hình vuông
Bài 6:
a: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM\(\perp\)BC
Vì M là trung điểm của BC
nên \(MB=MC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right)\)
Ta có: ΔAMB vuông tại M
=>\(AM^2+MB^2=AB^2\)
=>\(AM^2+6^2=10^2\)
=>\(AM^2+36=100\)
=>\(AM^2=100-36=64\)
=>\(AM=\sqrt{64}=8\left(cm\right)\)
b: Xét tứ giác AMCK có
I là trung điểm chung của AC và MK
=>AMCK là hình bình hành
Hình bình hành AMCK có \(\widehat{AMC}=90^0\)
nên AMCK là hình chữ nhật
c: AMCK là hình chữ nhật
=>AK//CM và AK=CM
Ta có: AK//CM
M\(\in\)BC
Do đó: AK//MB
Ta có: AK=CM
CM=MB
Do đó: AK=MB
Xét tứ giác AKMB có
AK//MB
AK=MB
Do đó: AKMB là hình bình hành
d: Để hình chữ nhật AMCK trở thành hình vuông thì AM=CM
mà \(CM=\dfrac{BC}{2}\)
nên \(AM=\dfrac{BC}{2}\)
Xét ΔABC có
AM là đường trung tuyến
\(AM=\dfrac{BC}{2}\)
Do đó: ΔABC vuông tại A
=>\(\widehat{BAC}=90^0\)
Đúng 1
Bình luận (0)
câu này đề cương trường thcs long bình dễ mà cx đi hỏi à s gà v
Đúng 0
Bình luận (0)
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146): a) Tính thể tích khoảng không ở bên trong lều. b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu? (Không tính các mép và nếp gấp của lều). Hình 146
Đọc tiếp
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146):
a) Tính thể tích khoảng không ở bên trong lều.
b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu?
(Không tính các mép và nếp gấp của lều).
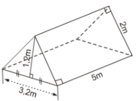
Hình 146
Một chiếc lều trại có hình dạng và kích thước như Hình 11. Tính tổng diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) và thể tích của chiếc lều.
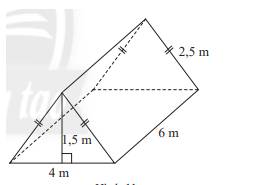
Diện tích tấm bạt có thể phủ kín toàn bộ lều (không tính mặt tiếp giáp với đất) là:
S = Sxq + 2.Sđáy - \(S_{đất}\)= (4+2,5+2,5).6 + 2 .\(\dfrac{1}{2}\).4.1,5 - 6.4= 36 (m2)
Thể tích của chiếc lều là:
V = Sđáy . h =\(\dfrac{1}{2}\) .4.1,5 . 6 = 18 (m3)
Đúng 0
Bình luận (0)
Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 6 mét, đỉnh trại cách nền 3 mét. Tính thể tích phần không gian bên trong lều trại. A. 72 B.
72
π
C. 36 D.
36
π
Đọc tiếp
Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có dạng hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 6 mét, đỉnh trại cách nền 3 mét. Tính thể tích phần không gian bên trong lều trại.
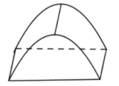
A. 72
B. 72 π
C. 36
D. 36 π

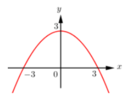
Cách giải:
Gắn hệ trục tọa độ như hình vẽ.
Gọi phương trình parabol là: y = a x 2 + b x + c

Đúng 0
Bình luận (0)
Một cái lều ở trại hè có dạng lăng trụ đứng tam giác (với các kích thước trên hình 146)

a) Tính thể tích khoảng không ở bên trong lều
b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu ?
(Không tính các mép và nếp gấp của lều)
a) Lều là lăng trụ đứng tam giác.
Diện tích đáy (tam giác):
S=12.3,2.1,2=1,92(m2)S=12.3,2.1,2=1,92(m2)
Thể tích khoảng không bên trong lều là:
V = Sh = 1,92. 5 = 9,6 (m3)
b) Số vải bạt cần có để dựng lều chính là diện tích toàn phần của lăng trụ trừ đi diện tích mặt bên có kích thước là 5m và 3,2m.
Diện tích xung quanh lăng trụ là:
Sxq = 2ph = (2 + 2+ 3,2) .5 = 36 (m2)
Diện tích toàn phần:
Stp = Sxq + 2Sđ = 36 + 2.1,92 = 39,84 (m2)
Diện tích mặt bên kích thước 5m và 3,2m là:
S = 5.3,2 = 16 (m2)
Vậy số vải bạt cần có để dựng lều là:
39,84 – 16 = 23,84 (m2)
Chú ý:Có thể tính bằng cách khác là tổng diện tích hai mặt bên và hai đáy.
Đúng 0
Bình luận (0)
Một lều trại có dạng hình lăng trụ đứng đặt nằm ngang. Đáy của hình lăng trụ (tức hai đầu hổi của lều) có hình dạng là các tam giác cân, cạnh đáy của các tam giác cân này tiếp giáp mặt đât và có độ dài 3 m, chiều cao tương ứng dài 2m. Chiều cao lăng trụ (tức chiều dài của lều trại) bằng 4m.a) Tính diện tích bạt phủ hai mái lều.b) Tính thê tích của lều trại
Đọc tiếp
Một lều trại có dạng hình lăng trụ đứng đặt nằm ngang. Đáy của hình lăng trụ (tức hai đầu hổi của lều) có hình dạng là các tam giác cân, cạnh đáy của các tam giác cân này tiếp giáp mặt đâ't và có độ dài 3 m, chiều cao tương ứng dài 2m. Chiều cao lăng trụ (tức chiều dài của lều trại) bằng 4m.
a) Tính diện tích bạt phủ hai mái lều.
b) Tính thê tích của lều trại
a) Tính được diện tích bạt phủ 2 mái lều: 20 (m2)
b) Thể tích của leeud trại là: V = 12 (m3)
Đúng 0
Bình luận (0)
Hình 149 là chiếc lều ở một trại hè với các kích thước cho trên hình. ABC là một tam giác vuông cân
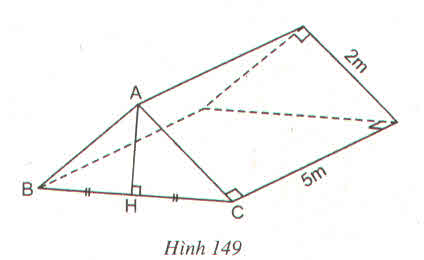
a) Tính thể tích của lều
b) Số vải bạt cần phải có để dựng lều đó là bao nhiêu ?
(Không tính các mép gấp, đương viền,.....)
Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 6 mét, đỉnh trại cách nền 3 mét. Tính thể tích phần không gian bên trong trại. A. . B. . C. . D. .
Đọc tiếp
Để chuẩn bị cho hội trại do Đoàn trường tổ chức, lớp 12A dự định dựng một cái lều trại có hình parabol như hình vẽ. Nền của lều trại là một hình chữ nhật có kích thước bề ngang 3 mét, chiều dài 6 mét, đỉnh trại cách nền 3 mét. Tính thể tích phần không gian bên trong trại.
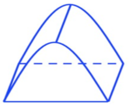
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.






















