a: (2x+1)(3-x)(4-2x)=0

=>(2x+1)(x-3)(x-2)=0

hay \(x\in\left\{-\dfrac{1}{2};3;2\right\}\)

b: 2x(x-3)+5(x-3)=0

=>(x-3)(2x+5)=0

=>x=3 hoặc x=-5/2

c: =>(x-2)(x+2)+(x-2)(2x-3)=0

=>(x-2)(x+2+2x-3)=0

=>(x-2)(3x-1)=0

=>x=2 hoặc x=1/3

d: =>(x-2)(x-3)=0

=>x=2 hoặc x=3

e: =>(2x+5+x+2)(2x+5-x-2)=0

=>(3x+7)(x+3)=0

=>x=-7/3 hoặc x=-3

f: \(\Leftrightarrow2x^3+5x^2-3x=0\)

\(\Leftrightarrow x\left(2x^2+5x-3\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(2x-1\right)=0\)

hay \(x\in\left\{0;-3;\dfrac{1}{2}\right\}\)

1) (x+6)(3x-1)+x+6=0

⇔(x+6)(3x-1)+(x+6)=0

⇔(x+6)(3x-1+1)=0

⇔3x(x+6)=0

2) (x+4)(5x+9)-x-4=0

⇔(x+4)(5x+9)-(x+4)=0

⇔(x+4)(5x+9-1)=0

⇔(x+4)(5x+8)=0

3)(1-x)(5x+3)÷(3x-7)(x-1)

=\(\frac{\left(1-x\right)\left(5x+3\right)}{\left(3x-7\right)\left(x-1\right)}=\frac{\left(1-x\right)\left(5x+3\right)}{\left(7-3x\right)\left(1-x\right)}=\frac{\left(5x+3\right)}{\left(7-3x\right)}\)

2: \(3x\left(x-4\right)+2x-8=0\)

=>\(3x\left(x-4\right)+2\left(x-4\right)=0\)

=>\(\left(x-4\right)\left(3x+2\right)=0\)

=>\(\left[{}\begin{matrix}x-4=0\\3x+2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-\dfrac{2}{3}\end{matrix}\right.\)

3: 4x(x-3)+x²-9=0

=>\(4x\left(x-3\right)+\left(x+3\right)\left(x-3\right)=0\)

=>\(\left(x-3\right)\left(4x+x+3\right)=0\)

=>\(\left(x-3\right)\left(5x+3\right)=0\)

=>\(\left[{}\begin{matrix}x-3=0\\5x+3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{3}{5}\end{matrix}\right.\)

4: \(x\left(x-1\right)-x^2+3x=0\)

=>\(x^2-x-x^2+3x=0\)

=>2x=0

=>x=0

5: \(x\left(2x-1\right)-2x^2+5x=16\)

=>\(2x^2-x-2x^2+5x=16\)

=>4x=16

=>x=4

Answer:

\(\left(2x-3\right).\left(x+1\right)-x.\left(2x+3\right)-9=0\)

\(\Rightarrow\left(2x^2+2x-3x-3\right)-2x^2-3x-9=0\)

\(\Rightarrow\left(2x^2-x-3\right)-2x^2-3x-9=0\)

\(\Rightarrow2x^2-x-3-2x^2-3x-9=0\)

\(\Rightarrow\left(2x^2-2x^2\right)-\left(x+3x\right)-\left(3+9\right)=0\)

\(\Rightarrow-4x-12=0\)

\(\Rightarrow x+3=0\)

\(\Rightarrow x=-3\)

\(2x.\left(x-3\right)-x+3=0\) (Sửa đề)

\(\Rightarrow2x.\left(x-3\right)-\left(x-3\right)=0\)

\(\Rightarrow\left(x-3\right).\left(2x-1\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-3=0\\2x-1=0\end{cases}\Rightarrow\orbr{\begin{cases}x=3\\2x=1\end{cases}}\Rightarrow\orbr{\begin{cases}x=3\\x=\frac{1}{2}\end{cases}}}\)

\(2x.\left(x^2-4\right)+6.\left(4-x^2\right)=0\)

\(\Rightarrow2x.\left(x^2-4\right)-6.\left(x^2-4\right)=0\)

\(\Rightarrow2.\left(x-3\right).\left(x+2\right).\left(x-2\right)=0\)

Trường hợp 1: \(x-3=0\Rightarrow x=3\)

Trường hợp 2: \(x+2=0\Rightarrow x=-2\)

Trường hợp 3: \(x-2=0\Rightarrow x=2\)

( 2x - 3 )( x + 1 ) - 2x² + 6x = 0

<=> 2x² - x - 3 - 2x² + 6x = 0

<=> 5x - 3 = 0

<=> 5x = 3

<=> x = 3/5

( x² - x + 1 )( x - 3 ) - x³ + 4x² = 0

<=> x³ - 4x² + 4x - 3 - x³ + 4x² = 0

<=> 4x - 3 = 0

<=> 4x = 3

<=> x = 3/4

( x² - 2 )( x² + 2 ) - x⁴ - 2x + 5 = 0

<=> ( x² )² - 4 - x⁴ - 2x + 5 = 0

<=> x⁴ + 1 - x⁴ - 2x = 0

<=> 1 - 2x = 0

<=> 2x = 1

<=> x = 1/2

( x - 3 )( x² - 3x + 2 ) - ( x² - 2x - 7 )( x - 2 ) + 2x² - 2x = 0

<=> x³ - 6x² + 11x - 6 - ( x³ - 4x² - 3x + 14 ) + 2x² - 2x = 0

<=> x³ - 6x² + 11x - 6 - x³ + 4x² + 3x - 14 + 2x² - 2x = 0

<=> 12x - 20 = 0

<=> 12x = 20

<=> x = 20/12 = 5/3

a, \(\left(2x-3\right)\left(x+1\right)-2x^2+6x=0\)

\(\Leftrightarrow2x^2+2x-3x-3-2x^2+6x=0\Leftrightarrow5x-3=0\Leftrightarrow x=\frac{3}{5}\)

b, \(\left(x^2-x+1\right)\left(x-3\right)-x^3+4x^2=0\)

\(\Leftrightarrow x^3-3x^2-x^2+3x+x-3-x^3+4x^2=0\Leftrightarrow4x-3=0\Leftrightarrow x=\frac{3}{4}\)

c ; d tương tự nhé ! 

a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27

⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27

⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29

⇔ -2x – 3x = 24 – 29

⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1

Tập nghiệm của phương trình : S = {1}

b) x2 – 4 – (x + 5)(2 – x) = 0

⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0

⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0

⇔ x = 2 hoặc x = -7/2

Tập nghiệm của phương trình: S = {2; -7/2 }

c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)

⇔ x ≠ 2 và x ≠ -2

Quy đồng mẫu thức hai vế :

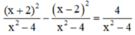
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4

⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)

Tập nghiệm của phương trình : S = {1/2}

d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)

⇔ x ≠ 1 và x ≠ -3

Quy đồng mẫu thức hai vế :

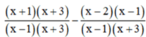
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0

⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)

Tập nghiệm của phương trình : S = ∅

\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)

\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)

\(< =>2x^2-2x-24=2x^2+3x-2-27\)

\(< =>5x=-24+29=5\)

\(< =>x=\frac{5}{5}=1\)

\(x^2-4-\left(x+5\right)\left(2-x\right)=0\)

\(< =>\left(x-2\right)\left(x+2\right)+\left(x+5\right)\left(x-2\right)=0\)

\(< =>\left(x-2\right)\left(x+2+x+5\right)=0\)

\(< =>\left(x-2\right)\left(2x+7\right)=0\)

\(< =>\orbr{\begin{cases}x-2=0\\2x+7=0\end{cases}}< =>\orbr{\begin{cases}x=2\\x=-\frac{7}{2}\end{cases}}\)

\(a,x^4-2x^3+5x^2-10x=0\\ \Leftrightarrow x^3\left(x-2\right)+5x\left(x-2\right)=0\\ \Leftrightarrow x\left(x^2+5\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x^2+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\\x\in\varnothing\left(x^2+5>0\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

\(b,\left(3x+5\right)^2=\left(2x-2\right)^2\\ \Leftrightarrow\left(3x+5\right)^2-\left(2x-2\right)^2=0\\ \Leftrightarrow\left(3x+5+2x-2\right)\left(3x+5-2x+2\right)=0\\ \Leftrightarrow\left(5x+3\right)\left(x+7\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{5}\\x=-7\end{matrix}\right.\)

\(c,x^3-2x^2+x=0\\ \Leftrightarrow x\left(x-1\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

\(d,x^2\left(x-1\right)-4x^2+8x-4=0\\ \Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a) \(x^4-2x^3+5x^2-10x=0\\ \Rightarrow\left(x^4-2x^3\right)+\left(5x^2-10x\right)=0\\ \Rightarrow x^3\left(x-2\right)+5x\left(x-2\right)=0\\ \Rightarrow\left(x^3+5x\right)\left(x-2\right)=0\\ \Rightarrow x\left(x^2+5\right)\left(x-2\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x^2+5=0\\x-2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=\pm\sqrt{5}\\x=2\end{matrix}\right.\)

Vậy \(x=\left\{-\sqrt{5};0;\sqrt{5};2\right\}\)

b) \(\left(3x+5\right)^2=\left(2x-2\right)^2\\ \Rightarrow\left[{}\begin{matrix}3x+5=2x-2\\3x+5=-2x+2\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-7\\x=-\dfrac{3}{5}\end{matrix}\right.\)

c) \(x^3-2x^2+x=0\\ \Rightarrow x\left(x^2-2x+1\right)=0\\ \Rightarrow x\left(x-1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\\left(x-1\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)

vậy ...

d) \(x^2\left(x-1\right)-4x^2+8x-4=0\\ x^2\left(x-1\right)-\left(4x^2-8x+4\right)=0\\ x^2\left(x-1\right)-\left(2x-2\right)^2=0\\ \Rightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Rightarrow\left(x-1\right)\left[x^2-4\left(x-1\right)\right]=0\\ \Rightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Rightarrow\left(x-1\right)\left(x-2\right)^2=0\)

    \(\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-2\right)^2=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

a: Ta có: \(x^4-2x^3+5x^2-10x=0\)

\(\Leftrightarrow x\left(x^3-2x^2+5x-10\right)=0\)

\(\Leftrightarrow x\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)

b:Ta có: \(\left(3x+5\right)^2=\left(2x-2\right)^2\)

\(\Leftrightarrow\left(3x+5\right)^2-\left(2x-2\right)^2=0\)

\(\Leftrightarrow\left(3x+5-2x+2\right)\left(3x+5+2x-2\right)=0\)

\(\Leftrightarrow\left(x+7\right)\left(5x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-7\\x=-\dfrac{3}{5}\end{matrix}\right.\)

      c.   x^2-5x +6 = 0

<=> x^2 - 5x = -6

<=> - 4x = -6

<=> x= -6/-4

 Mình chỉ phân tích đa thức thành nhân tử thôi , phần còn lại bạn tự tính nha keo dài lắm

A)  2x²(x+3) - x(x+3) = 0  <=> x(x - 3)(2x-1)=0

B)  (2x+5)² - (x+2)²=0  <=>  (x+3)(3x+7)=0

C)  (x²-2x) - (3x-6)=0  <=> (x-2)(x-3)=0

D)  (2x-7)(2x-7-6x+18)=0   <=> (2x-7)(-4x+11)=0

E)  (x-2)(x+1) - (x-2)(x+2)=0   <=>  (x-2)*(-1)=0   <=> x-2=0

G)  (2x-3)(2x+2-5x)=0  <=> (2x-3)(-3x+2)=0

H)  (1-x)(5x+3+3x-7)=0     <=>  (1-x)(8x-4)=0

F)   (x+6)*3x=0

I)  (x-3)(4x-1-5x-2)=0  <=>  (x-3)(-x-3)=0

K)   (x+4)(5x+8)=0

H)  (x+3)(4x-9)=0

B> <2X+5>²-<X+2>²=0

<2X+5-X-2><2X+X+2>=0

<X+3><3X+7>=0

X+3=0 HOẶC 3X+7=0

X=-3 HOẶC X=-7/3

C>X²-5X+6=0

X²-4X+4-X+2=0

<X-2>²-<X-2>=0

<X-2.><X-3>=0

X-2=0 HOẶC X-3=0

X=2 HOẶC X=3

D> <2X-7><2X-7-6<X-3>>=0

<2X-7><-4X+11>=0

2X-7=0 HOẶC -4X+11=0

X=7/2 HOẶC X=11/4

E><X-2><X+1>=X²-4

<X-2><X+1>-<X²-4>=0

<X-2><X+1>-<X-2><X+2>=0

-X+2=0

X=2

CÒN NHIÊU TỰ LÀM ĐI MỆT WA