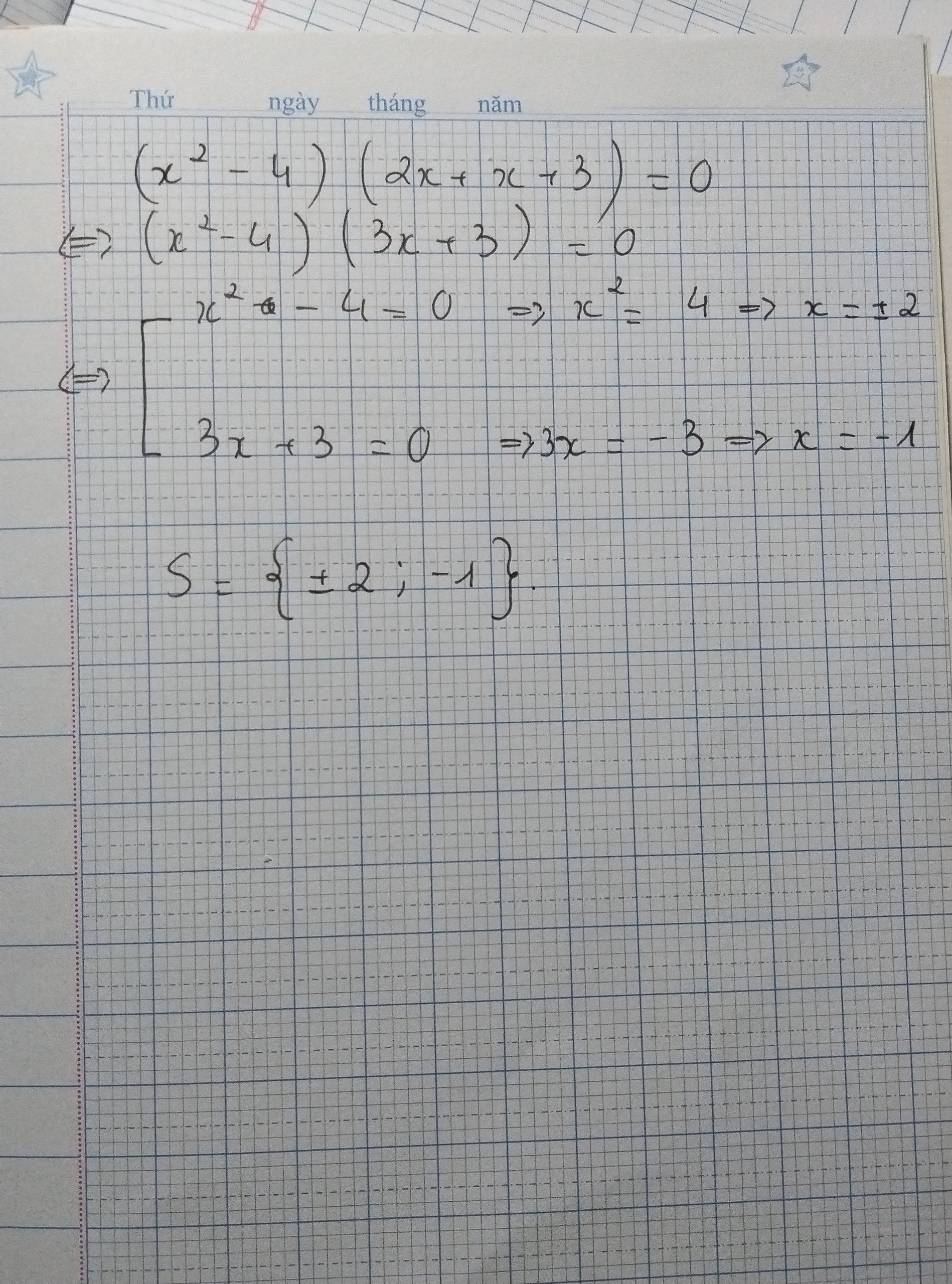(x² - 4)(2x + x + 3) = 0
(x² - 4)(3x + 3) = 0
x² - 4 = 0 hoặc 3x + 3 = 0
*) x² - 4 = 0
x² = 4
x = 2 hoặc x = -2
*) 3x + 3 = 0
3x = -3
x = -3 : 3
x = -1
Vậy x = -2; x = -1; x = 2
Ta thấy 2 nhân tử trong ngoặc tròn bên trái đều có thể chia thành nhân tử đơn giản hơn như sau: x^2 - 4 = (x + 2)(x - 2) 2x + x + 3 = 3x + 3 Vậy phương trình trở thành: (x + 2)(x - 2)(3x + 3) = 0 Để tích bằng 0, ta cần ít nhất một trong 3 nhân tử bằng 0. Do đó ta có ba phương trình con: x + 2 = 0 ⇔ x = -2 x - 2 = 0 ⇔ x = 2 3x + 3 = 0 ⇔ x = -1 Vậy phương trình có ba nghiệm: x = -2, x = 2, x = -1