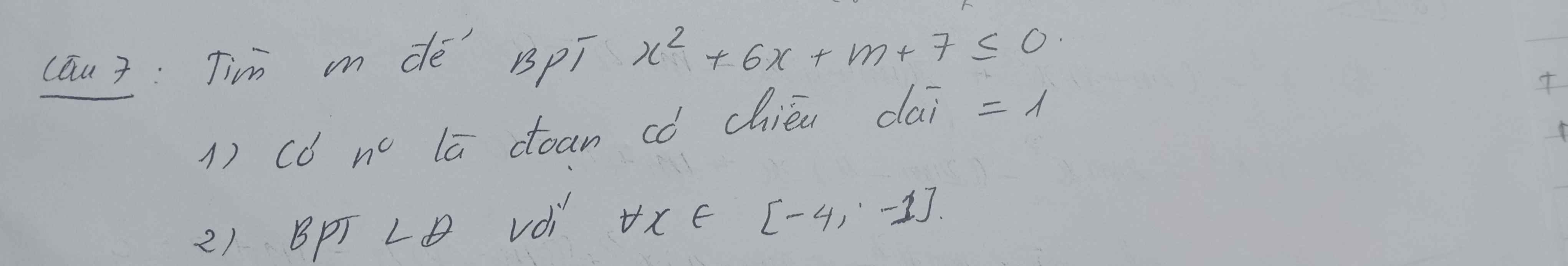
a. Gọi \(x_1>x_2\) là 2 nghiệm của \(x^2+6x+m+7=0\) thì BPT đã cho có tập nghiệm là đoạn có chiều dài bằng 1 khi và chỉ khi \(x_1-x_2=1\)

\(\Leftrightarrow\left(x_1-x_2\right)^2=1\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=1\)

\(\Leftrightarrow36-4\left(m+7\right)=1\)

\(\Leftrightarrow m=\dfrac{7}{4}\)

b. \(x^2+6x+m+7\le0\) ;\(\forall x\in\left[-4;-1\right]\)

\(\Leftrightarrow x^2+6x+7\le-m\) ; \(\forall x\in\left[-4;-1\right]\)

\(\Leftrightarrow-m\ge\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)\)

Xét hàm \(f\left(x\right)=x^2+6x+7\) trên \(\left[-4;-1\right]\)

\(-\dfrac{b}{2a}=-3\in\left[-4;-1\right]\) ; \(f\left(-4\right)=-1\) ; \(f\left(-3\right)=-2\) ; \(f\left(-1\right)=2\)

\(\Rightarrow\max\limits_{\left[-4;-1\right]}\left(x^2+6x+7\right)=2\Rightarrow-m\ge2\)

\(\Rightarrow m\le-2\)

\(\left(-3\right)^2+\sqrt{16}-3-\dfrac{\sqrt{81}}{\left|-3\right|}\\ =9+4-3-3\\ =7\)

c: \(\left(-3\right)^2+\sqrt{16}-3-\dfrac{\sqrt{81}}{\left|-3\right|}\)

\(=9+4-3-\dfrac{9}{3}\)

\(=10-3=7\)

Tham khảo!

Câu 3:

 Khi bão, mưa to, ngập lụt, sạt lở đất, lốc xoáy,…đã qua, nhân dân vùng ảnh hưởng thiên tai cần chủ động:

      Nhanh chóng đưa người bị thương đến trạm xá, bệnh viện, tìm kiếm người còn bị mất tích.

      Thông báo cho chính quyền địa phương, hoặc đơn vị điện lực, viễn thông biết nếu có dây cáp bị hư hại hoặc cột điện đổ.

      Cẩn thận chú ý các động vật nguy hiểm như rắn có thể bò vào nhà. 

      Sửa chữa, dọn dẹp và vệ sinh nhà cửa, nước rút đến đâu, lau rửa nhà đến đó ; chôn xác gia súc, gia cầm bị chết; nhớ rắc vôi hoặc phun thuốc khử trùng nơi gia súc gia cầm chết và nơi chôn gia súc gia cầm để xử lí mầm bệnh. 

      Sử dụng nước sạch để ăn, uống; nếu không có nước sạch mà phải dùng nước sông, ao, hồ thì phải lọc và đun sôi kỹ.

      Nhanh chóng khôi phục chăn nuôi, sản xuất đảm bảo đời sống sau thiên tai

bạn có thể ghi lại câu 4 ko mình ko hiểu??

Tham khảo!

Bước 1: Khảo sát

- Tìm hiểu các yêu cầu của công tác quản lí.

- Xác định và phân tích mối liên hệ các dữ liệu cần lưu trữ.

- Phân tích các chức năng cần có của hệ thống khai thác thông tin, đáp ứng các yêu cầu đặt ra.

- Xác định khả năng phần cứng, phần mềm có thể khai thác, sử dụng.

Bước 2: Thiết kế

- Thiết kế CSDL.

- Lựa chọn hệ quản trị để triển khai.

- Xây dựng hệ thống chương trình ứng dụng.

Bước 3: Kiểm thử

- Nhập dữ liệu cho CSDL.

- Tiến hành chạy thử các chương trình ứng dụng.

\(5;;\sqrt{\left(x+5\right)\left(3x+4\right)}>4\left(x-1\right)\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\end{matrix}\right.\)

\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\le0\\\left(x+5\right)\left(3x+4\right)\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow x\in(-\infty;-5]\cup\left[-\dfrac{4}{3};1\right]\left(1\right)\)

\(TH:\left\{{}\begin{matrix}4\left(x-1\right)\ge0\\\left(x+5\right)\left(3x+4\right)\ge0\\\left(x+5\right)\left(3x+4\right)>16\left(x-1\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge1\\\left[{}\begin{matrix}x\le-5\\x\ge-\dfrac{4}{3}\end{matrix}\right.\\-\dfrac{1}{13}< x< 4\\\end{matrix}\right.\)\(\Rightarrow x\in[1;4)\left(2\right)\)

\(\left(1\right)\left(2\right)\Rightarrow x\in(-\infty;5]\cup[\dfrac{-4}{3};4)\)

\(6;;;;\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{49x^2+7x-42}< 181-14x\)

(đoạn 49x^2+7x+42 chắc bạn viết sai đề dấu"-" thành "+")

\(đk:\left\{{}\begin{matrix}7x+7\ge0\\7x-6\ge0\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{6}{7}\)

\(bpt\Leftrightarrow\sqrt{7x+7}+\sqrt{7x-6}+2\sqrt{\left(7x+7\right)\left(7x-6\right)}+14x+1< 182\left(1\right)\)

\(đặt:\sqrt{7x+7}+\sqrt{7x-6}=t>0\)

\(\Rightarrow t^2=14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}\)

\(\Rightarrow\left(1\right)\Leftrightarrow t^2+t< 182\Leftrightarrow-14< t< 13\)

\(\Rightarrow\sqrt{7x+7}+\sqrt{7x-6}< 13\Leftrightarrow14x+1+2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 169\)

\(\Leftrightarrow2\sqrt{\left(7x+7\right)\left(7x-6\right)}< 168-14x\)

\(\Leftrightarrow\left\{{}\begin{matrix}168-14x\ge0\\\left(7x+7\right)\left(7x-6\right)\ge0\\4\left(7x+7\right)\left(7x-6\right)< \left(168-14x\right)^2\\\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\le12\\\left[{}\begin{matrix}x\le-1\\x\ge\dfrac{6}{7}\end{matrix}\right.\\x< 6\\\end{matrix}\right.\)\(\Rightarrow\dfrac{6}{7}\le x< 6\)

\(7;\) \(3\sqrt{x}+\dfrac{3}{2\sqrt{x}}< 2x+\dfrac{1}{2x}-1\left(đk:x>0\right)\)

\(\Leftrightarrow3\left(\sqrt{x}+\dfrac{1}{2\sqrt{x}}\right)< 2\left(x+\dfrac{1}{4x}\right)-1\left(1\right)\)

\(đặt:\sqrt{x}+\dfrac{1}{2\sqrt{x}}=t>0\)

\(\Leftrightarrow t^2=\sqrt{x}^2+2.\sqrt{x}.\dfrac{1}{2\sqrt{x}}+\left(\dfrac{1}{2\sqrt{x}}\right)^2=x+\dfrac{1}{4x}+1\)

\(\Rightarrow x+\dfrac{1}{4x}=t^2-1\)

\(\left(1\right)\Leftrightarrow3t< 2\left(t^2-1\right)-1\)

\(\Leftrightarrow2t^2-3t-3>0\Leftrightarrow\left[{}\begin{matrix}t< \dfrac{3-\sqrt{33}}{4}\\t>\dfrac{3+\sqrt{33}}{4}\end{matrix}\right.\)

\(\Rightarrow\sqrt{x}+\dfrac{1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)

\(\Leftrightarrow\dfrac{2x+1}{2\sqrt{x}}>\dfrac{3+\sqrt{33}}{4}\)

\(\Leftrightarrow\sqrt{x}< \dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\Leftrightarrow\left\{{}\begin{matrix}x>0\\2\left(2x+1\right)\ge0\\x< \left[\dfrac{2\left(2x+1\right)}{3+\sqrt{33}}\right]^2\\\end{matrix}\right.\)

đến đây dễ dàng rồi như mấy ý trên bạn tự giải quyết để tìm ra x

a, xét \(\Delta ABC\left(\widehat{BAC}=90^o\right)\) có \(AM\) là đường cao
\(BC^2=AB^2+AC^2\left(pytago\right)\Leftrightarrow BC=\sqrt{12^2+16^2}=20\left(cm\right)\)
\(sinABC=\dfrac{AC}{BC}=\dfrac{16}{20}\Rightarrow\widehat{ABC}\approx53^o8'\)
\(sinACB=\dfrac{AB}{BC}=\dfrac{12}{20}\Rightarrow\widehat{ACB}\approx32^o52'\)
\(AB^2=BM.BC\Rightarrow BM=\dfrac{AB^2}{BC}=\dfrac{12^2}{20}=7,2\left(cm\right)\)
b, Xét \(\Delta ABM\left(\widehat{AMB}=90^o\right)\) có \(AE\perp AB\)
\(AB^2=BM^2+AM^2\left(pytago\right)\Leftrightarrow AM=\sqrt{20^2-7,2^2}=\dfrac{16\sqrt{34}}{5}\left(cm\right)\)
\(AM^2=AE.AB\) (hệ thức lượng trong tam giác vuông)\(\left(1\right)\)
c, Xét \(\Delta AMC\left(\widehat{AMC}=90^o\right)\)
\(AC^2=AM^2+MC^2\left(pytago\right)\Leftrightarrow AM^2=AC^2-MC^2\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow AE.AB=AC^2-MC^2\left(đpcm\right)\)