Tính độ dài cạnh AB trong mỗi trường hợp sau:

cho tam giác ABC vuông tại A, tính độ dài cạnh BC trong trường hợp sau : AB = 2AC và AB + AC
Tính độ dài mỗi cạnh của 1 sân hình vuông có diện tích lần lượt là 16m2 ; 6,25m2 ; 6m2 . Trong mỗi trường hợp, hãy cho biết độ dài mỗi cạnh được biểu diễn bằng số hữu tỉ hay vô tỉ
gọi độ dài mỗi cạnh của sân là x ( x > 0 )
Ta lần lượt :
a) x2 = 16 \(\Rightarrow\text{ }x=\sqrt{16}=4\left(m\right)\text{ };\text{ }4\in Q\)
b) x2 = 6,25 \(\Rightarrow\text{ }x=\sqrt{6,25}=2,5\left(m\right)\text{ };\text{ }\text{ }2,5\in Q\)
c) x2 = 6 \(\Rightarrow\text{ }x=\sqrt{6}\approx2,45\left(m\right)\text{ };\text{ }\sqrt{6}\in I\)
Bài 5. Bộ ba số đo độ dài nào trong mỗi trường hợp sau là độ dài ba cạnh của một tam giác? a) 12cm; 8cm; 6cm. b) 4 cm; 8cm; 12cm. Bài 6. Cho AABC có ba góc nhọn, kẻ BD – AC tại D, CE 1. AB tại E. a) Chứng minh: AB + AC > BD +CE. b) Chứng minh: BC> BD+CE
2
Đề bài: Cho tam giác ABC vuông tại A, đường cao AH. Tính độ dài các cạnh còn lại của tam giác ABC trong mỗi trường hợp sau:
a. AB = a, AH = \(\dfrac{a\sqrt{3}}{2}\)
b. BC = 2a, HB = \(\dfrac{1}{4}BC\)
c. AB = a, CH = \(\dfrac{3}{2}a\)
d. CA = \(a\sqrt{3}\), AH = \(\dfrac{a\sqrt{3}}{2}\)
Giúp mình với ạ, mình cảm ơn trước.
a.
Áp dụng hệ thức lượt trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\Leftrightarrow \frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{3a^2}$
$\Rightarrow AC=\sqrt{3}a$
$BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+3a^2}=2a$
b.
$HB=\frac{BC}{4}$ thì $HC=\frac{3}{4}BC$
$\Rightarrow \frac{HB}{HC}=\frac{1}{3}$
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC; AC^2=CH.BC$
$\Rightarrow \frac{AB}{AC}=\sqrt{\frac{BH}{CH}}=\frac{\sqrt{3}}{3}$
Áp dụng định lý Pitago:
$4a^2=BC^2=AB^2+AC^2=(\frac{\sqrt{3}}{3}.AC)^2+AC^2$
$\Rightarrow AC=\sqrt{3}a$
$\Rightarrow AB=a$
c.
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC$
$\Leftrightarrow AB^2=BH(BH+CH)$
$\Leftrightarrow a^2=BH(BH+\frac{3}{2}a)$
$\Leftrightarrow BH^2+\frac{3}{2}aBH-a^2=0$
$\Leftrightarrow (BH-\frac{a}{2})(BH+2a)=0$
$\Rightarrow BH=\frac{a}{2}$
$BC=BH+CH=2a$
$AC=\sqrt{BC^2-AB^2}=\sqrt{3}a$
d. Tương tự phần a.
Tính thể tích tứ diện SABC trong mỗi trường hợp sau :
a, SABC là hình chóp đều, cạnh đáy=a, góc giữa mặt bên và cạnh đáy =45 độ.
b,Các cạnh bên cùng tạo với đáy góc 60 độ, AB=5a, BC=6a, CA=7a.
c, mp(SAB) vuông góc với mp(ABC), tam giác ABC là tam giác đều có cạnh=a, góc giữa SC và mp(ABC)=30 độ.
d,góc giữa các mặt bên và mặt đáy = nhau=60 độ, tam giác ABC có AB=a,AC=2a, góc A=60 độ .
e, SA vuông góc với mp(ABC), SA=a, góc giữa (SBC) và đáy là 60 độ
Có hay không một tam giác mà độ dài ba cạnh của tam giác đó được cho bởi các độ dài trong mỗi trường hợp sau?
a) 8 cm, 5 cm, 3 cm;
b) 12 cm, 6 cm, 6 cm;
c) 15 cm, 9 cm, 4 cm.
a) Ta thấy:
\(\begin{array}{l}8 - 5 = 3 = 3\end{array}\)
Vậy bộ ba số đo độ dài 8 cm, 5 cm, 3 cm không thể là độ dài ba cạnh của một tam giác.
b) Ta thấy:
\(\begin{array}{l}12 - 6 = 6\end{array}\)
Vậy bộ ba số đo độ dài 12 cm, 6 cm, 6 cm không thể là độ dài ba cạnh của một tam giác.
c) Ta thấy: \(15 - 9 = 6 > 4\).
Vậy bộ ba số đo độ dài 15 cm, 9 cm, 4 cm không thể là độ dài ba cạnh của một tam giác.
Cho tam giác ABC vuông tại A, đường cao AH. Biết tỉ số giữa 2 cạnh góc vuông AB : AC là 3 : 4. Tính các độ dài đoạn thẳng chưa biết trong các trường hợp sau:
BC = 125cm AH = 12cmBH = 18cmĐường trung tuyến ứng với cạnh huyền dài 100cmCho tứ diện ABCD có AB = x thay đổi, tất cả các cạnh còn lại có độ dài a. Tính khoảng cách giữa hai đường thẳng AB và CD trong trường hợp thể tích của khối tứ diện ABCD lớn nhất.
A. a 3 3
B. a 6 4
C. a 3 4
D. a 6 3
Đáp án B
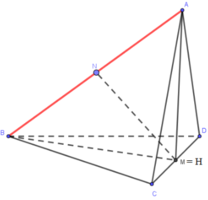
Cách giải:
Gọi M là trung điểm của CD. Kẻ AH vuông góc mặt phẳng (BCD) (H thuộc (BCD)) ⇒ H ∈ BM, AH ⊥ HM
VABCD lớn nhất khi và chỉ khi AH có độ dài lớn nhất, tức là khi H trùng M
Hai tam giác ACD, BCD đều, cạnh a, có đường cao AM, BM bằng a 3 2
Tam giác ABM vuông cân tại A, lấy N là trung điểm của AB ⇒ MN ⊥ AB
Mà MN ⊂ (AMB) ⊥ CD ⇒ MN ⊥ CD ⇒ MN là đoạn vuông góc chung của AB và CD
Khoảng cách giữa hai đường thẳng AB và CD là:
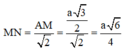
Một khung dây hình chữ nhật ABCD đặt trong từ trường đều cảm ứng từ B = 5 . 10-4 ( T ) . Cạnh AB của khung dài 3 cm , cạnh BC dài 5 cm . Dòng điện trong khung có cường độ 2 A . Tính giá trị lớn nhất của momen ngẫu lực từ tác dụng lên khung trong hai trường hợp .
a) Cạnh AB của khung vuông góc còn cạnh BC song song với đường sức từ.
b) Cạnh BC của khung vuông góc còn cạnh AB song song với đường sức từ .
Trả lời:
a) Giá trị lớn nhất của momen ngẫu lực từ tác dụng lên khung khi cạnh AB của khung vuông góc còn cạnh BC song song với đường sức từ:
M = IBS = 2.5.10-4.15.10-4 = 15.10-7 (Nm)
b) Giá trị lớn nhất của momen ngẫu lực từ tác dụng lên khung khi cạnh BC của khung vuông góc với đường sức từ còn cạnh AB song song với đường sức từ:
M = IBS = 2.5.10-4.15.10-4 = 15.10-7 (Nm)
Chúc bạn học tốt!![]()
a) Giá trị lớn nhất của momen ngẫu lực từ tác dụng lên khung khi cạnh AB của khung vuông góc còn cạnh BC song song với đường sức từ :
M = IBS = 2 . 5 . 10-4 . 15 . 10-4 = 15 . 10-7 ( N . m )
b) Giá trị lớn nhất của momen ngẫu lực từ tác dụng lên khung khi cạnh BC của khung vuông góc với đường sức từ còn cạnh AB song song với đường sức từ :
M = IBS = 2 . 5 . 10-4 . 15 . 10-4 = 15 . 10-7 ( N . m )