Cho tam giác ABC có \(AB = c, Ac = b, BC = a\). Viết công thức tính cos A.

Những câu hỏi liên quan
Cho tam giác ABC có \(AB = c, AC = b, \widehat A = \alpha \). Viết công thức tính BC theo \(b,c,\alpha \)
Áp dụng định lí cosin trong tam giác ABC ta có:
\(B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\)
\(\begin{array}{l} \Leftrightarrow B{C^2} = {c^2} + {b^2} - 2.c.b.\cos \alpha \\ \Leftrightarrow BC = \sqrt {{c^2} + {b^2} - 2bc.\cos \alpha } \end{array}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH
a) Viết công thức tính diện tích tam giác ABC
b) Cho AB = 6 cm, BC = 10 cm. Tính AC, AH, DT tam giác ABC
a) công thức . \(\frac{đáy.chiềucao}{2}\)
b) Áp dụng định lý pitago ta có
\(BC^2=AB^2+AC^2\)
=> AC^2=\(BC^2-AB^2=^{10^2}-6^2=64\)
=>\(AC=8\)
A)Xét tam giác ABC vuông tại A(gt),có:
SABC=(AB.AC)/2
B)Xét tam giác ABC vuông tại A(gt),có:
AB^2+AC^2=BC^2(ĐL Pytago)
Thay số:36+AC^×=100
<=>AC=căn64=8cm
Ta có:SABC=(AB.AC)/2
Thay số:SABC=24cm^2
Mà SABC=(AH.BC)/2
=>(AH.BC)/2=24
Thay số:AH=24.2:10=4,8cm
SABC=24CM^2(cmt)
Cho tam giác ABC. Giá trị nhỏ nhất của biểu thức \(Q=\dfrac{bc.\cos A+ac.\cos B+ab.\cos C}{S}\) bằng bao nhiêu ?
\(bc.cosA=bc\left(\dfrac{b^2+c^2-a^2}{2bc}\right)=\dfrac{b^2+c^2-a^2}{2}\)
Tương tự: \(ac.cosB=\dfrac{a^2+c^2-b^2}{2}\) ; \(ab.cosC=\dfrac{a^2+b^2-c^2}{2}\)
\(\Rightarrow Q=\dfrac{a^2+b^2+c^2}{2S}\ge\dfrac{\left(a+b+c\right)^2}{6S}=\dfrac{4p^2}{6\sqrt{p\left(p-a\right)\left(p-b\right)\left(p-c\right)}}\)
\(Q\ge\dfrac{2p\sqrt{p}}{3\sqrt{\left(p-a\right)\left(p-b\right)\left(p-c\right)}}\ge\dfrac{2p\sqrt{p}}{3\sqrt{\left(\dfrac{3p-\left(a+b+c\right)}{3}\right)^3}}=\dfrac{2p\sqrt{p}}{3\sqrt{\dfrac{p^3}{27}}}=2\sqrt{3}\)
Đúng 1
Bình luận (0)
cho tam giác abc có A^=90 độ AB= 6cm và AC = 8cm a/ tính Bc? b/ tính sin B và Tan C? C/ gọi AH là đường cao tam giác ABC , tính cos BAH^,d/ Gọi M là trung điểm Bc từ M kẻ đường thẳng vuông góc với BC cắt AC tại T tính độ dài AT?
a: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=10(cm)
Đúng 0
Bình luận (0)
1. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=4cm,AC=9cm. Tính sin B, sin C
2.Cho tam giác ABC vuông tại A, Cos B= an pha, Cos = 4/5. Tính sin, tan,cos
3. Cho tam giác ABC vuông tại A, đường cao AH, biết AB=6cm, BC= 10cm
a. Tính AC,AH. Tỉ số đồng giác góc B,C
b. Gọi E,F lần lượt là hình chiếu H lên AB,AC. CM :AE.AD=AF.AC
c. Tính S tứ giác AEHF
a) Cho tam giác ABC đều. Tính giá trị biểu thức Pcosleft(overrightarrow{AB},overrightarrow{BC}right)+cosleft(overrightarrow{BC},overrightarrow{CA}right)+cosleft(overrightarrow{CA},overrightarrow{AB}right)b) Cho cung lượng giác có số đo x thỏa mãn tan x 2. Giá trị biểu thức Adfrac{sin x-cos x}{sin x+cos x}c) Giá trị biểu thức Adfrac{cosleft(750right)+sinleft(420right)}{sinleft(-330right)-cosleft(-390right)}
Đọc tiếp
a) Cho tam giác ABC đều. Tính giá trị biểu thức \(P=\cos\left(\overrightarrow{AB},\overrightarrow{BC}\right)+\cos\left(\overrightarrow{BC},\overrightarrow{CA}\right)+\cos\left(\overrightarrow{CA},\overrightarrow{AB}\right)\)
b) Cho cung lượng giác có số đo x thỏa mãn tan x =2. Giá trị biểu thức \(A=\dfrac{\sin x-\cos x}{\sin x+\cos x}\)
c) Giá trị biểu thức \(A=\dfrac{\cos\left(750\right)+\sin\left(420\right)}{\sin\left(-330\right)-\cos\left(-390\right)}\)
a.
\(P=cos120^0+cos120^0+cos120^0=-\dfrac{3}{2}\)
b.
\(A=\dfrac{\dfrac{sinx}{cosx}-\dfrac{cosx}{cosx}}{\dfrac{sinx}{cosx}+\dfrac{cosx}{cosx}}=\dfrac{tanx-1}{tanx+1}=\dfrac{2-1}{2+1}=\dfrac{1}{3}\)
c.
\(A=\dfrac{cos\left(720+30\right)+sin\left(360+60\right)}{sin\left(-360+30\right)-cos\left(-360-30\right)}=\dfrac{cos30+sin60}{sin30-cos30}=-3-\sqrt{3}\)
Đúng 3
Bình luận (0)
Cho tam giác ABC có BC = a, AC = b, AB = c và (I;r) là đường tròn nội tiếp tam giác (Hình 11).
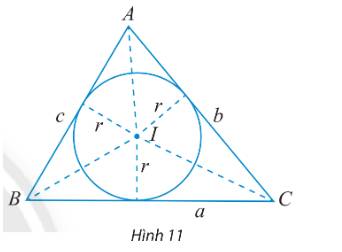
a) Tính diện tích các tam giác IBC, IAC, IAB theo r và a, b, c.
b) Dùng kết quả trên để chứng minh công thức tính diện tích tam giác ABC: \(S = \frac{{r(a + b + c)}}{2}\)
a) Diện tích \({S_1}\) của tam giác IAB là: \({S_1} = \frac{1}{2}r.AB = \frac{1}{2}r.c\)
Diện tích \({S_2}\) của tam giác IAC là: \({S_2} = \frac{1}{2}r.AC = \frac{1}{2}r.b\)
Diện tích \({S_3}\) của tam giác IBC là: \({S_3} = \frac{1}{2}r.BC = \frac{1}{2}r.a\)
b) Diện tích S của tam giác ABC là:
\(\begin{array}{l}S = {S_1} + {S_2} + {S_3} = \frac{1}{2}r.c + \frac{1}{2}r.b + \frac{1}{2}r.a = \frac{1}{2}r.(c + b + a)\\ \Leftrightarrow S = \frac{{r(a + b + c)}}{2}\end{array}\)
Đúng 0
Bình luận (0)
Từ định lí cosin hãy viết các công thức tính cos A, cos B, cos C theo độ dài các cạnh a, b, c của tam giác ABC.
Định lí cosin: Trong tam giác ABC
\(\begin{array}{l}{a^2} = {b^2} + {c^2} - \,2b\,c.\cos A\quad (1)\\{b^2} = {a^2} + {c^2} - \,2a\,c.\cos B\quad (2)\\{c^2} = {b^2} + {a^2} - \,2ab.\cos C\quad (3)\end{array}\)
Ta có \((1) \Leftrightarrow 2bc\cos A = {b^2} + {c^2} - {a^2}\, \Leftrightarrow \cos A = \frac{{{b^2} + {c^2} - {a^2}\,}}{{2b\,c}}.\)
Tương tự từ (2) và (3) ta suy ra \(\cos B = \frac{{{a^2} + {c^2} - {b^2}\,}}{{2a\,c}}\); \(\cos C = \frac{{{b^2} + {a^2} - {c^2}\,}}{{2b\,a}}\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A. Đường cao AH. Biết AB = 7,5 cm; AH =6cm . Tính AC; BC ; cos B ; cos C
\(AB^2=AH.BC\Rightarrow BC=\frac{AB^2}{AH}=\frac{7,5^2}{6}=9,375\)
áp dụng định lí Pytago tính được AC = 5,625
tính cosB và cos C thì quá dễ rồi. bạn làm tiếp nhé
Đúng 0
Bình luận (0)













