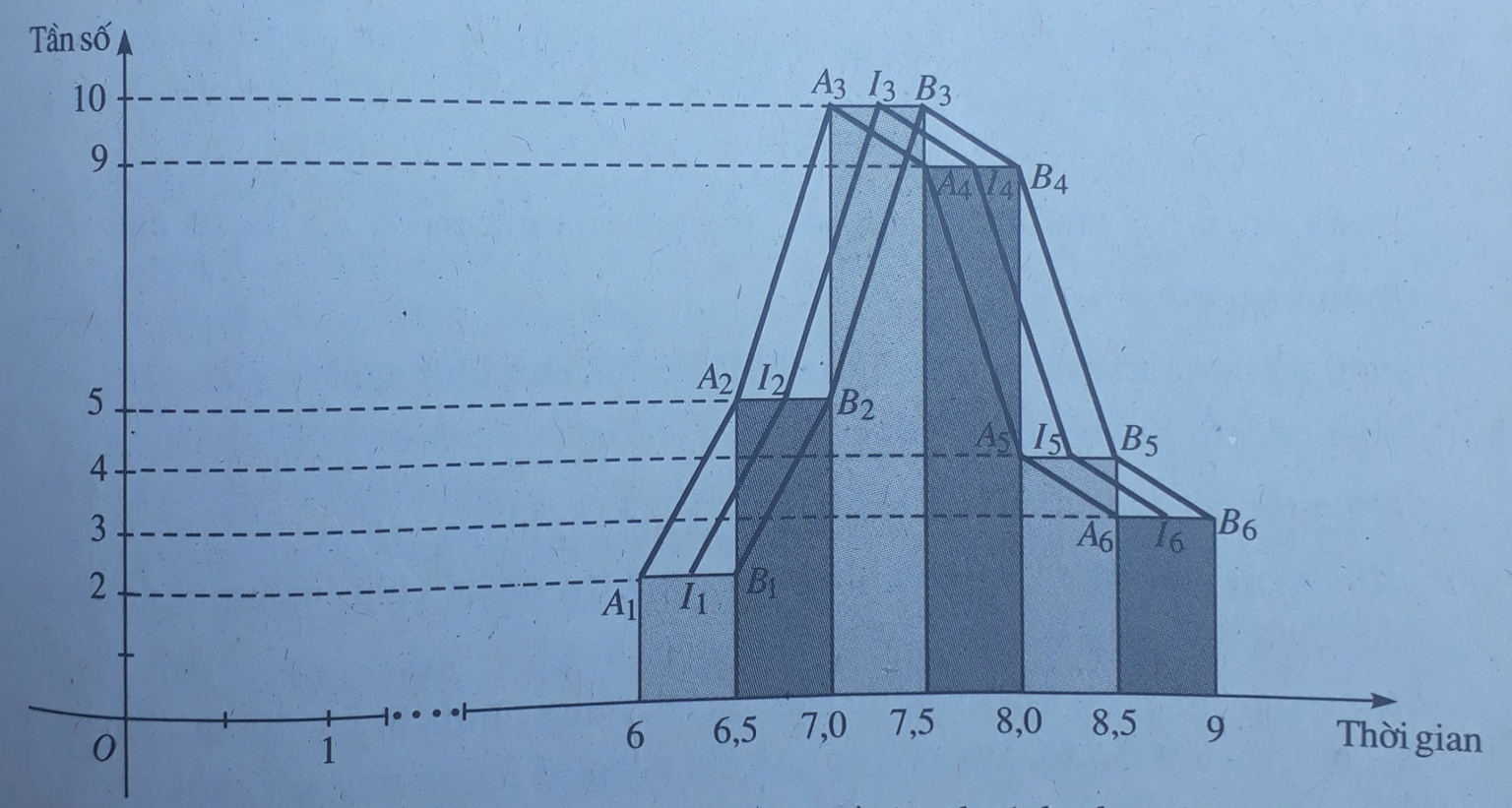
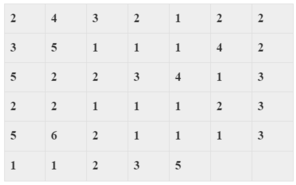
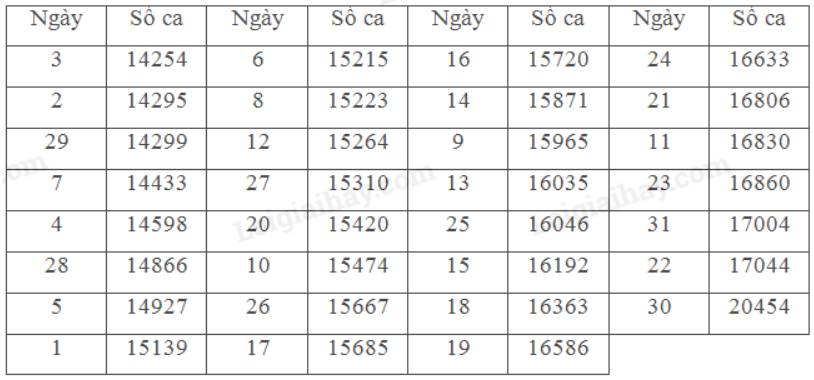
Xét dữ liệu cho trong tình huống mở đầu.
a) Mẫu số liệu về tổng điểm, kí hiệu là (T), có bao nhiêu giá trị?
b) Nếu lập bảng tần số cho mẫu số liệu (T) thì có dễ hình dung được bức tranh tổng thể về kết quả thi không? Vì sao?
c) Mẫu số liệu (T) được mô tả dưới dạng bảng thống kê sau: