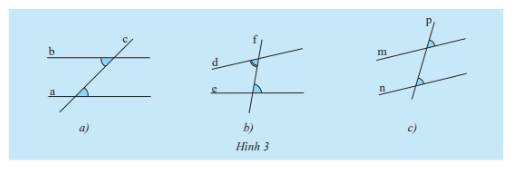
Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
Đọc tiếp
Quan sát Hình 3 và dự đoán các đường thẳng nào song song với nhau.
Những câu hỏi liên quan
Quan sát các Hình 38a, 38b, 38c và đoán xem các đường thẳng nào song song với nhau.
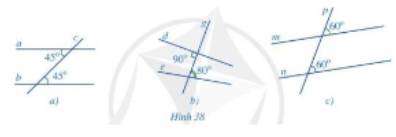
Hình 38a: a và b song song
Hình 38b: không có 2 đường thẳng nào song song
Hình 38c: m và n song song
Đúng 0
Bình luận (0)
Cho điểm A nằm ngoài đường thẳng a, quan sát cách vẽ đường thẳng b đi qua A và song song với a ở Hình 8
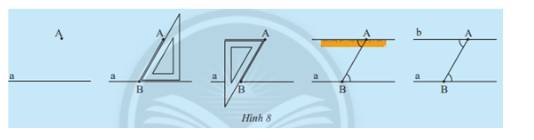
Em hãy dự đoán xem có bao nhiêu đường thẳng b đi qua A và song song với đường thẳng a
Có chỉ 1 đường thẳng b đi qua A và song song với đường thẳng a
Đúng 1
Bình luận (0)
quan sát xung quanh và chỉ ra hình ảnh của các đường thẳng song song hay các đường thẳng vuông góc với nhau
Xem hình 17 (a, b, c). Đoán xem các đường thẳng nào song song với nhau.
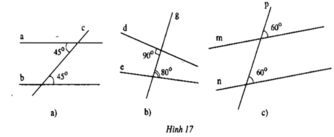
Các đường thẳng song song với nhau là a và b ; m và n
Đúng 0
Bình luận (0)
Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB. Qua D vẽ đường thẳng song song với BC, đường thẳng này cắt AC ở E. Bằng quan sát, hãy nêu dự đoán về vị trí của điểm E trên cạnh AC.
Cho đoạn thẳng CD và đường thẳng m song song với CD (h.29). Hãy vẽ các điểm A, B thuộc m sao cho ABCD là hình thang có hai đường chéo CA, DB bằng nhau. Sau đó hãy đo các góc C ̂ và D ̂ của hình thang ABCD đó để dự đoán về dạng của các hình thang có đường chéo bằng nhau.
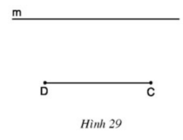
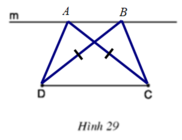
Hai góc C và D bằng nhau
⇒ Hình thang có hai đường chéo bằng nhau là hình thang cân
Đúng 0
Bình luận (0)
làm cm ra rõ hơn ko
Quan sát Hình 36 và chỉ ra: 
a) Các cặp đường thẳng song song.
b) Các cặp đường thẳng cắt nhau.
a) a//b; b//c; a//c; d//e
b) a cắt d; a cắt e
b cắt d; b cắt e
c cắt d, c cắt e
Đúng 1
Bình luận (0)
1. Quan sát Hình 3.22 và giải thích vì sao AB // CD.
2. Tìm trên Hình 3.23 hai đường thẳng song song với nhau và giải thích vì sao chúng song song?
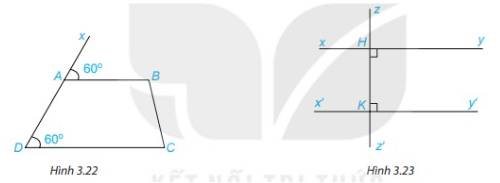
1. Vì \(\widehat {BAx} = \widehat {CDA}( = 60^\circ )\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) AB//CD (Dấu hiệu nhận biết hai đường thẳng song song)
2. Ta có: \(\widehat {zKy'} + \widehat {y'Kz'} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow 90^\circ + \widehat {y'Kz'} = 180^\circ \\ \Rightarrow \widehat {y'Kz'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Vì \(\widehat {yHz'} = \widehat {y'Kz'}\)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow \) xy // x’y’ (Dấu hiệu nhận biết hai đường thẳng song song)
Chú ý:
2 đường thẳng cùng vuông góc với 1 đường thẳng thứ ba thì 2 đường thẳng đó song song.
Đúng 0
Bình luận (0)
Giải mục 1 trang 95, 96, 97 SGK Toán 11 tập 1 - Cánh Diều
14 tháng 7 2023 lúc 16:03
Trong không gian, cho điểm M và đường thẳng d không đi qua điểm M (Hình 36). Nêu dự đoán về số đường thẳng đi qua điểm M và song song với đường thẳng d.
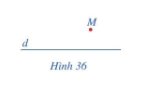
Có một và chỉ một đường thẳng đi qua điểm M và song song với đường thẳng d
Đúng 0
Bình luận (0)