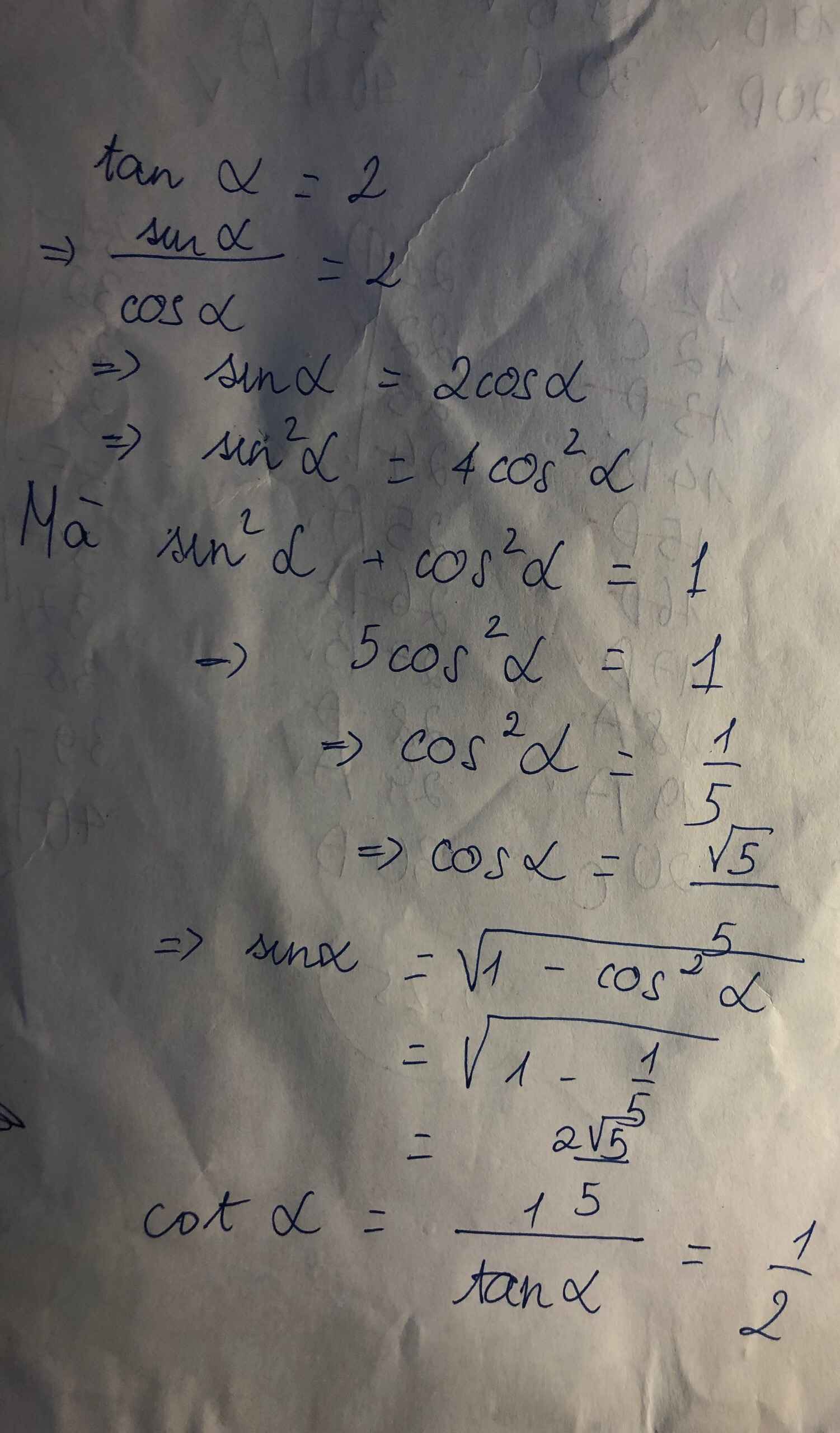Cho biết \({153^2} = 23409\). Hãy tính \(\sqrt {23409} \)

Những câu hỏi liên quan
Cho biết 153²=23 409. Hãy tính √23 409
a/ Không sử dụng máy tính .Cho góc nhọn α , biết sinα = \(\dfrac{\sqrt{3}}{2}\) . Hãy tính cosα ; tanα ; cotα.
b/ Không sử dụng máy tính .Cho góc nhọn α , biết cosα = \(\dfrac{\sqrt{5}}{7}\) . Hãy tính cosα ; tanα ; cotα.
a: \(\cos\alpha=\dfrac{1}{2}\)
\(\tan\alpha=\sqrt{3}\)
\(\cot\alpha=\dfrac{\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Không cần tính kết quả cụ thể , các bạn hãy cho biết 2 tổng sau có bằng nhau không ? Vì sao
a = 123 + 456 + 78 + 90
b = 498 + 76 + 153 + 20
-_-????
a = 123 + 456 + 78 + 90
= 100 + 20 + 3 + 400 + 50 + 6 + 70 + 8 + 90
b = 498 + 76 + 153 + 20
= 400 + 90 + 8 + 70 + 6 + 100 + 3 + 20
a = b vì các số đều giống nhau
Đúng 0
Bình luận (0)
a=123+456+76+20+(2+70) =123+456+76+20 + 72
b=123+456+76+20+(20+42)=123+456+76+20 + 62
vậy 2 tổng trên ko bằng nhau
Đúng 0
Bình luận (0)
a=123+456+76+20+(2+70) =123+456+76+20 + 72
b=123+456+76+20+(20+42)=123+456+76+20 + 62
vậy 2 tổng trên ko bằng nhau
Đúng 0
Bình luận (0)
Cho \(A=\dfrac{1}{\sqrt{x}-2}\) So sánh \(\sqrt{A}\) và\(A^2\) biết x thỏa mãn \(x^2+14x-5x\sqrt{x}-153\sqrt{x}+452=0\)
tồn tại \(\sqrt{A}\Rightarrow x>4\)
\(B=x^2+14x-5x\sqrt{x}-153\sqrt{x}+452\)
\(B=\left(\sqrt{x}-4\right)\left(x\sqrt{x}-x+10\sqrt{x}-113\right)\)
khi
\(0\le x< 16\Rightarrow\left\{{}\begin{matrix}\sqrt{x}-4< 0\\x\sqrt{x}-x+10\sqrt{x}-113< 64+40-113-x=-9-x< 0\end{matrix}\right.\) B>0
hay B không có nghiệm khi x<16
Kết luận x>16 \(\Rightarrow\sqrt{x}-2>1\Rightarrow\dfrac{1}{\sqrt{x}-2}< 1\Rightarrow A< 1\Rightarrow A^4< A< \sqrt{A}\)
Đúng 0
Bình luận (0)
cho biết \(\left(\sqrt{a^2+1}-a\right)\left(\sqrt{b^2+1}-b\right)=1\) 1. hãy tính tổng a + b.
Hình như a+b=0
bai nay nhan lien hop voi tung thua so ben ve trai la ra
KQ: a+b=0
chuc ban thanh cong
Bài 1: Biết sinα = \(\dfrac{\sqrt{3}}{2}\). Hãy tính cosα, tanα, cotα.
Bài 2: Biết tanα = 2. Hãy tính sinα, cotα, cosα
Bài 3: Tính: A= cos2 20o + cos2 40o + cos2 50o + cos2 70o
Bài 3:
Ta có: \(A=\cos^220^0+\cos^240^0+\cos^250^0+\cos^270^0\)
\(=\left(\sin^270^0+\cos^270^0\right)+\left(\sin^250^0+\cos^250^0\right)\)
=1+1
=2
Đúng 0
Bình luận (0)
Bài 2: Trong các số 4510; 2075; 23409; 301200, số vừa chia hết cho 3 vừa chia hết cho 5 nhưng không chia hết cho 9 là: A. 4510 B. 2075 C. 301200 D. 23409
Đọc tiếp
Bài 2: Trong các số 4510; 2075; 23409; 301200, số vừa chia hết cho 3 vừa chia hết cho 5 nhưng không chia hết cho 9 là:
A. 4510 B. 2075 C. 301200 D. 23409
Tl
C.301200
HT
Không thực hiện phép tính, hãy cho biết chữ số hàng đơn vị của mỗi kết quả sau:
a) (151 + 152 + 153 + …. + 159) – (63 +23 + 37)
b) (511 + 512 + 513 + …. + 519) - 92 x 73 x 55 x 37 x 19
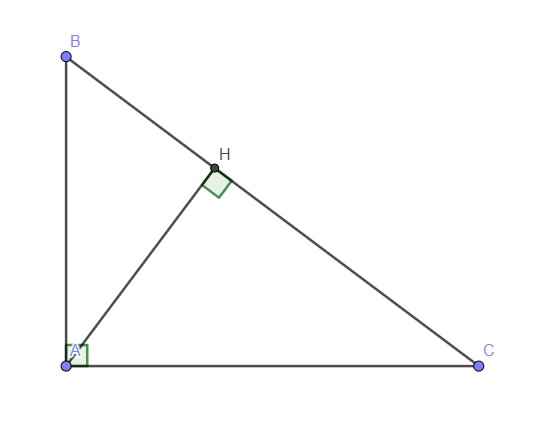
Cho tam giác ABC vuông ở A, tanB = \(\sqrt{2}\) .
a) Tính tỉ số lượng giác của góc C.
b) Kẻ AH vuông góc với BC, biết AH = 2\(\sqrt{3}\) cm . Hãy tính các cạnh của tam giác ABC.
giúp e vs ạ
\(tanB=\sqrt{2}\Rightarrow\dfrac{AC}{AB}=\sqrt{2}\Rightarrow\dfrac{AC^2}{AB^2}=2\)
\(\Rightarrow\dfrac{AC^2}{AB^2}+1=3\Rightarrow\dfrac{AC^2+AB^2}{AB^2}=3\Rightarrow\dfrac{BC^2}{AB^2}=3\)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}\)
Mà \(sinC=\dfrac{AB}{BC}\Rightarrow sinC=\dfrac{1}{\sqrt{3}}\)
\(sin^2C+cos^2C=1\Rightarrow\dfrac{1}{3}+cos^2C=1\Rightarrow cosC=\dfrac{\sqrt{6}}{3}\)
\(tanC=\dfrac{sinC}{cosC}=\dfrac{\sqrt{2}}{2}\)
b.
Trong tam giác vuông ACH:
\(sinC=\dfrac{AH}{AC}\Rightarrow AC=\dfrac{AH}{sinC}=\dfrac{2\sqrt{3}}{\dfrac{1}{\sqrt{3}}}=6\left(cm\right)\)
Trong tam giác vuông ABC:
\(tanB=\dfrac{AC}{AB}\Rightarrow AB=\dfrac{AC}{tanB}=\dfrac{6}{\sqrt{2}}=3\sqrt{2}\)
Áp dụng Pitago:
\(BC=\sqrt{AB^2+AC^2}=3\sqrt{6}\left(cm\right)\)
Đúng 0
Bình luận (0)
a: Xét ΔABC vuông tại A có
\(\tan\widehat{B}=\sqrt{2}\)
\(\Leftrightarrow AC=AB\cdot\sqrt{2}\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3\cdot AB^2\)
hay \(BC=AB\cdot\sqrt{3}\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}\)
\(\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{\sqrt{2}}{\sqrt{3}}=\dfrac{\sqrt{6}}{3}\)
\(\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\cot\widehat{C}=\sqrt{2}\)
Đúng 0
Bình luận (0)