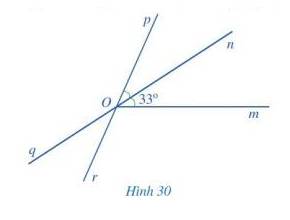
Trong Hình 30, tính số đo của \(\widehat {mOp};\widehat {qOr};\widehat {pOq}\)
Trong hình vẽ có góc MOP = 130 độ và góc M = 60 độ . Tính số đo góc của P để MN//PQ.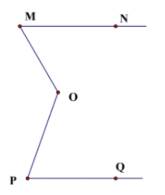
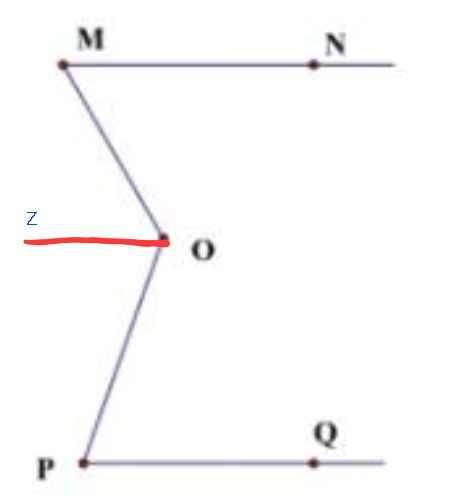 Vẽ tia Oz //MN
Vẽ tia Oz //MN
⇒ ∠MOz = ∠OMN = 60⁰
⇒ ∠zOP = ∠MOP - ∠MOz
= 130⁰ - 60⁰
= 70⁰
Để MN // PQ thì MN // Oz
⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)
Vẽ góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy vẽ hai tia Om, On sao cho \(\widehat{xOm}\) = 150° , \(\widehat{xOn}\) = 30° .
a) Tính số đo góc mOn
b) Vẽ tia Op là tia đối của tia On. Tia Oy có phải là tia phân giác của \(\widehat{mOp}\) không ? Vì sao ?
\(\widehat{XOM}\)= \(150^o\)
\(\widehat{XON}\) = \(30^o\)
Nên góc \(\widehat{MON}\) = \(\widehat{XOM}\) - \(\widehat{XON}\) = \(150^o\)- \(30^o\) = \(120^o\) Tia Oy là tia phân giác của góc \(\widehat{MOP}\)
VÌ tia Oy nằm giữa hai tia Om và Op , có chung một độ là \(30^o\) CHÚC BẠN THÀNH CÔNG
a. Ta có ; \(\widehat{mOn}=\widehat{xOm}-\widehat{xOn}\)
\(\Rightarrow\widehat{mOn}=150^o-30^o\)
\(\Rightarrow\widehat{mOn}=120^o\)
Vậy \(\widehat{mOn}=120^o\)
b . Ta có ; \(\widehat{yOm}=\widehat{xOy}-\widehat{xOm}\)
\(\Rightarrow\widehat{yOm}=180^o-150^o\)
\(\Rightarrow\widehat{yOm}=30^o\) \((1)\)
Mặt khác ; \(\widehat{yOp}=\widehat{xOn}\)\((\)đối đỉnh \()\)
mà bài cho \(\widehat{xOn}=30^o\)
\(\Rightarrow\widehat{yOp}=30^o\)\((2)\)
Từ \((1)\)và \((2)\)suy ra ;
\(\widehat{yOm}=\widehat{yOp}=30^o\)
\(\Rightarrow\)tia Oy là tia phân giác của \(\widehat{mOp}\)
Học tốt
Hãy chia tứ giác ABCD trong Hình 7 thành hai tam giác để tính tổng số đo của bốn góc \(\widehat A\),\(\widehat B\),\(\widehat C\),\(\widehat D\).
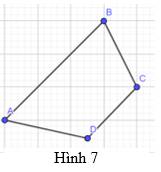
Ta chia tứ giác ABCD thành tam giác ACD và tam giác ABC
\( \Rightarrow \) Số đo tổng các góc tam giác ACD = tổng số đo các góc tam giác ABC = \({180^o}\)
\( \Rightarrow \)Tổng số đo các góc trong tứ giác ABCD = tổng số đo các góc 2 tam giác ACD và ABC \( = {2.180^o} = {360^o}\)
Biết rằng hai góc mOn và nOp kề bù, hơn nữa \(\widehat{mOn}=5\widehat{nOp}\). Khi đó :
(A) \(\widehat{mOn}=30^0\) và \(\widehat{mOp}=150^0\)
(B) \(\widehat{mOn}=150^0\) và \(\widehat{mOp}=30^0\)
(C) \(\widehat{mOn}=144^0\) và \(\widehat{mOp}=36^0\)
(D) \(\widehat{mOn}=36^0\) và \(\widehat{mOp}=144^0\)
Ở Hình 9, hai góc mOn và pOn có là hai góc kề nhau hay không? Tính số đo của góc mOp.
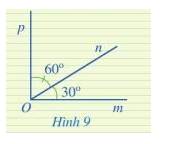
Hai góc mOn và pOn có là hai góc kề nhau vì có đỉnh O chung, cạnh On chung, 2 cạnh còn lại là Om và Op nằm về hai phía so với đường thẳng chứa On.
Vì On nằm trong góc mOp nên
\(\begin{array}{l}\widehat {mOn} + \widehat {nOp} = \widehat {mOp} \Rightarrow 30^\circ + 60^\circ = \widehat {mOp}\\ \Rightarrow 90^\circ = \widehat {mOp}\end{array}\)
Vậy \(\widehat {mOp} = 90^\circ \)
Cho Hình 16, biết a // b.
a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc \(\widehat {{B_2}}\)
b) Tính số đo các góc \(\widehat {{A_4}},\widehat {{A_2}},\widehat {{B_3}}\)
c) Tính số đo các góc \(\widehat {{B_1}},\widehat {{A_1}}\).
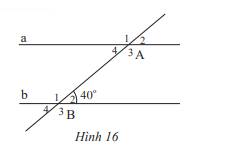
a) Góc ở vị trí so le trong với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_4}}\)
Góc ở vị trí đồng vị với góc \(\widehat {{B_2}}\) là: \(\widehat {{A_2}}\)
b) Vì a // b nên:
+) \(\widehat {{A_4}} = \widehat {{B_2}}\)( 2 góc so le trong), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_4}} = 40^\circ \)
+) \(\widehat {{A_2}} = \widehat {{B_2}}\) ( 2 góc đồng vị), mà \(\widehat {{B_2}} = 40^\circ \) nên \(\widehat {{A_2}} = 40^\circ \)
Ta có: \(\widehat {{B_2}} + \widehat {{B_3}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_3}} = 180^\circ \Rightarrow \widehat {{B_3}} = 180^\circ - 40^\circ = 140^\circ \)
c) Ta có: \(\widehat {{B_2}} + \widehat {{B_1}} = 180^\circ \) ( 2 góc kề bù) nên \(40^\circ + \widehat {{B_1}} = 180^\circ \Rightarrow \widehat {{B_1}} = 180^\circ - 40^\circ = 140^\circ \)
Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_1}}\) (2 góc đồng vị) nên \(\widehat {{A_1}} = 140^\circ \)
Hình 59 biểu diễn mặt cắt ngang của một con đê. Để đo góc nhọn MOP tạo bởi mặt nghiêng của con đê với phương nằm ngang, người ta dùng thước chữ T và đặt như hình vẽ ( \(OA\perp AB\)). Tính góc MOP, biết rằng dây dọi BC tạo với trục BA một góc \(\widehat{ABC}=32^0\)

Ta có tam giác ABC vuông ở A nên
\(\widehat{ABC}+\widehat{C}_1=90^0\)
Trong đó tam giác OCD vuông ở D có \(\widehat{MOP}=\widehat{C}_2=90^0\)
Nên \(\widehat{MOP}=\widehat{ABC}\)
\(\widehat{MOP}=32^0\)
Ta có tam giác ABC vuông ở A nên ∠ABC + ∠BCA = 900
Trong đó tam giác OCD vuông ở D có ∠COD + ∠OCD = 900
mà góc ∠BCA = ∠OCD ( 2 góc đối đỉnh)
Từ (1),(2),(3) ∠COD = ∠ABC mà ∠ABC= 320 . Nên ∠COD = 320
hay chính là ∠MOP =320
Cho góc MON có số đo bằng 155 độ, tia OP nằm trong góc MON. Biết góc PON có số đo bằng 70 độ. a) tính số đo của góc MOP. b)Vẽ tia OQ là tia đối của tia ON. Tính số đo góc QOM.
a)Có :\(\widehat{MOP}+\widehat{PON}=\widehat{MON}\)
\(\Rightarrow\widehat{MOP}+70^o=155^o\)
\(\Rightarrow\widehat{MOP}=85^o\)
b) Có :\(\widehat{QOM}+\widehat{MON}=180^o\)
\(\Rightarrow\widehat{QOM}+155^o=180^o\)
\(\Rightarrow\widehat{QOM}=25^o\)
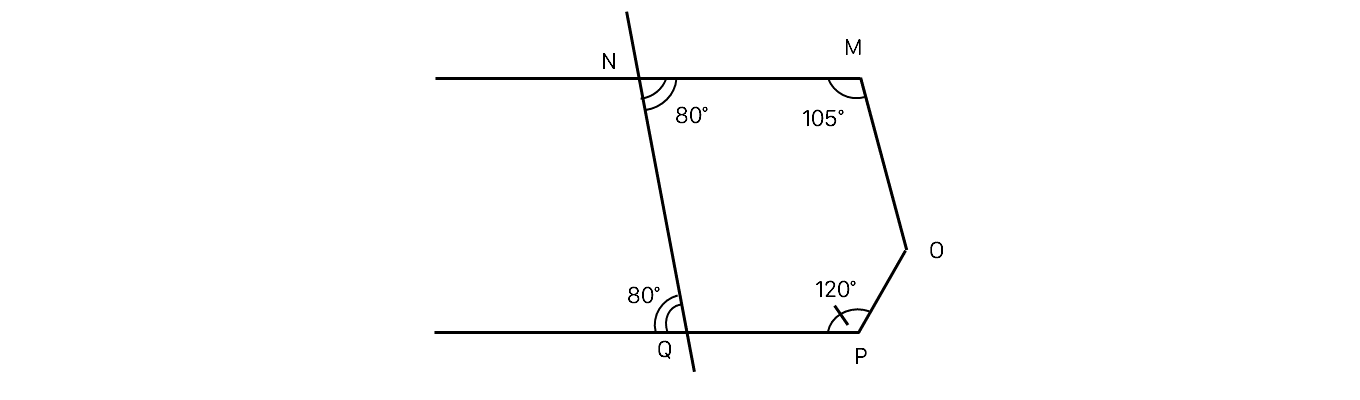
Cho hình vẽ, biết M= 105°, N = 80°,Q = 80°, P = 120°. Tính số đo góc MOP