Bài 1: Tìm ĐKXĐ của phân thức.
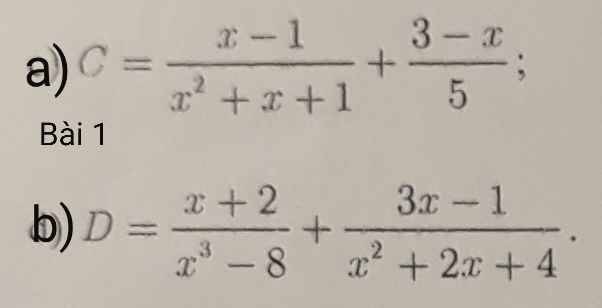
Bài 4: Cho phân thức
a) Tìm ĐKXĐ của D.
b) Hãy rút gọn phân thức D.
c) Tính giá trị của phân thức tại x = 2.
d) Tìm giá trị của x để giá trị của phân thức D > 2
`a)ĐKXĐ` của `D` la `x+2 \ne 0<=>x \ne -2`
`b)` Với `x \ne -2` có: `D=[2x^2-4x+8]/[x^3+8]`
`D=[2(x^2-2x+4)]/[(x+2)(x^2-2x+4)]=2/[x+2]`
`c)` Thay `x=2` vào `D` có: `D=2/[2+2]=1/2`
`d)D > 2<=>2/[x+2] > 2`
`<=>[2-2x-4]/[x+2] > 0`
`<=>[x+1]/[x+2] < 0<=>-2 < x <= -1`
Bài 1:cho phân thức :M=x2-1/x2+3x+2
a, tìm ĐKXĐ của phân thức
b,rút gọn phân thức giá trị M tại x=2002
c,tìm x để giá trị phan thức bằng 0
a: ĐKXĐ: \(x\notin\left\{-1;-2\right\}\)
b: \(M=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}=\dfrac{x-1}{x+2}\)
Thay x=2002 vào M, ta được:
\(M=\dfrac{2002-1}{2002+1}=\dfrac{2001}{2003}\)
c: Để M=0 thì x-1=0
hay x=1(nhận)
Bài 1:cho phân thức :M=x2-1/x2+3x+2
a, tìm ĐKXĐ của phân thức
b,rút gọn phân thức giá trị M tại x=2002
c,tìm x để giá trị phan thức bằng 0
Bài 3 Cho phân thức A= [3x^23x]/[x+1][3x-6]
a tìm ĐKXĐ VÀ rút A
b tính giá trị của A khi x=1/2
c tìm giá trị nguyên của x để phân thức A nhận giá trị nguyên
Bài 10: Cho biểu thức:A=x^2-1/x^2+3x+2
a, Tìm ĐKXĐ của x
b, Tính giá trị của phân thức tại x=2020
c, Tính giá trị của x để A=0
\(a,ĐK:x\ne-1;x\ne-2\\ b,A=\dfrac{\left(x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x+2\right)}=\dfrac{x-1}{x+2}\\ x=2020\Leftrightarrow A=\dfrac{2019}{2022}=\dfrac{673}{674}\\ c,A=0\Leftrightarrow x-1=0\Leftrightarrow x=1\left(tm\right)\)
Tìm đkxđ của phân thức: \(\dfrac{x^3+1}{x^2-x+1}\)
ĐKXĐ: \(x^2-x+1\ne0\)
=>\(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}\ne0\)
=>\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ne0\)(luôn đúng)
=>\(x\in R\)
giúp mình bài này vs ạ
bài 1:so sánh các căn sau
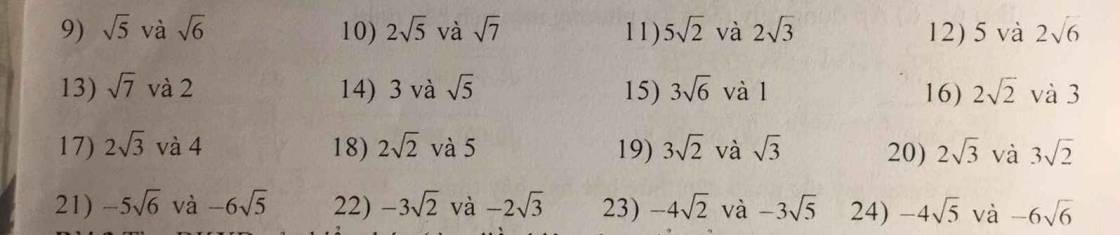
bài 2 :tìm ĐKXĐ của biểu thức (tìm đk của x để biểu thức sau có nghĩa)
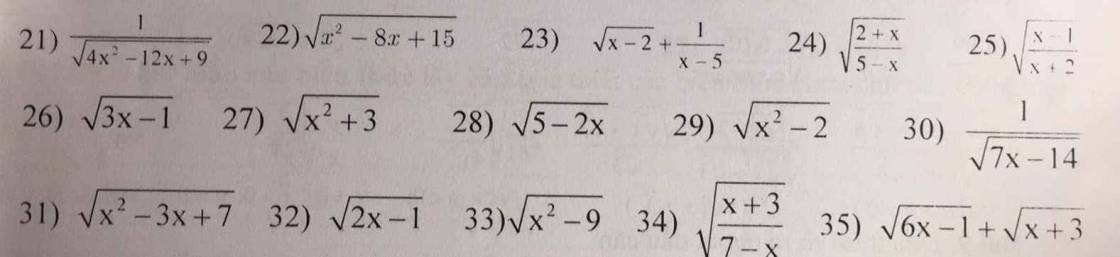
Bài 1
Mình làm mẫu một số câu thôi nhé
\(9,\sqrt{5}=\left(\sqrt{5}\right)^2=5\\ \sqrt{6}=\left(\sqrt{6}\right)^2=6\)
Vì \(5< 6\)
\(\Rightarrow\sqrt{5}< \sqrt{6}\)
\(10,2\sqrt{5}=\left(2\sqrt{5}\right)^2=20\\ \sqrt{7}=\left(\sqrt{7}\right)^2=7\)
Vì \(20>7\)
\(\Rightarrow2\sqrt{5}>\sqrt{7}\)
\(11,5\sqrt{2}=\left(5\sqrt{2}\right)^2=50\\ 2\sqrt{3}=\left(2\sqrt{3}\right)^2=12\)
Vì \(50>12\Rightarrow5\sqrt{2}>2\sqrt{3}\)
\(12,2\sqrt{6}=\left(2\sqrt{6}\right)^2=24\\ 5=5^2=25\)
Vì \(25>24\Rightarrow5>2\sqrt{6}\)
\(13,\sqrt{7}=\left(\sqrt{7}\right)^2=7\\ 2=2^2=4\)
Vì \(7>4\Rightarrow\sqrt{7}>2\)
\(14,3=3^2=9\\ \sqrt{5}=\left(\sqrt{5}\right)^2=5\)
Vì \(9>5\Rightarrow3>\sqrt{5}\)
\(15,3\sqrt{6}=\left(3\sqrt{6}\right)^2=54\)
Vì \(54>1\Rightarrow3\sqrt{6}>1\)
\(16,2\sqrt{2}=\left(2\sqrt{2}\right)^2=8\\ 3=3^2=9\)
Vì \(8< 9\Rightarrow2\sqrt{2}< 3\)
Phương pháp làm dạng bài này là bình phương hai vế rồi so sánh
Bài 2
Gợi ý : Biểu thức dưới dấu căn \(\ge\) 0
Lưu ý : Nếu biểu thức dưới dấu căn ở dưới mẫu thì \(>0\)
\(21,ĐK:4x^2-12x+9>0\\ \Rightarrow\left(2x-3\right)^2>0\\ \Leftrightarrow x\ne\dfrac{3}{2}\)
\(22,ĐK:x^2-8x+15\ge0\\ \Rightarrow\left[{}\begin{matrix}x\le3\\x\ge5\end{matrix}\right.\)
\(23,ĐK:\left\{{}\begin{matrix}x-2\ge0\\x-5\ne0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x\ge2\\x\ne5\end{matrix}\right.\)
\(24,ĐK:\left\{{}\begin{matrix}\dfrac{2+x}{5-x}\ge0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}2+x\ge0\\5-x\ge0\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x\le5\\x\ne5\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\ge-2\\x< 5\end{matrix}\right.\left(t/m\right)\)
Hoặc
\(\left\{{}\begin{matrix}2+x\le0\\5-x\le0\\5-x\ne0\end{matrix}\right.\\ \Rightarrow\left\{{}\begin{matrix}x\le-2\\x\ge5\\x\ne5\end{matrix}\right.\left(loại\right)\)
Chỉ đăng tối đa 10 - 15 câu hỏi thôi, câu trước GV nhắc bạn rồi mà giờ bạn vẫn còn đăng nữa thì nên bị xóa câu hỏi.
tìm ĐKXĐ của phân thức A = \(\dfrac{1}{x^2-xy+y^2}\)
cho phân thức c=16x^2-8x+1/4x^3-x^2
a)Tìm đkxđ của phân thức
b)Rút gọn
c)Tính giá trị của phân thức tại x=3
d)Tìm các giá trị của x để phân thức có giá trị = 0
a) x ≠ -5.
b) Ta có P = ( x + 5 ) 2 x + 5 = x + 5
c) Ta có P = 1 Û x = -4 (TMĐK)
d) Ta có P = 0 Û x = -5 (loại). Do vậy x ∈ ∅ .