Một hộp có chứa bốn cái thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2;3; 4 . hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên hai thẻ trong hộp. Tính xác xuất của biến cố “tích các số trên hai thẻ rút ra là số chẵn”.
Cần gấp ạ
Một hộp có bốn cái thẻ cùng loại, mỗi thẻ ghi một trong các số 5;6;7;8. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên hai thẻ trong hộp. Tính xác suất của biến cố “tích các số trên hai thẻ rút ra là số chẵn”. Trả lời: … Nhập kết quả dưới dạng phân số tối giản a/b.
Có 4 cách chọn thẻ thứ nhất. có 3 cách chọn thẻ thứ hai số cách chọn 2 tấm thẻ khác nhau từ 4 tấm thẻ là:
4 x 3 = 12 (cách)
Theo cách tính trên mỗi cách đã được tính hai lần. Vậy số cách lấy được 2 tấm thẻ từ bốn tấm thẻ đã cho là:
12 : 2 = 6 (cách)
Có 2 cách chọn tấm thẻ thứ nhất, có 3 cách chọn thẻ thứ hai. Vậy số cách chọn hai tấm thẻ để tích các số trên hai thẻ rút ra là số chẵn" là:
2 x 3 = 6 (cách)
Theo cách tính trên mỗi cách đã được tính hai lần.
Vậy số cách để rút hai tấm thẻ mà tích các số trên hai thẻ là số chẵn là:
6 : 2 = 3 (cách)
Xác suất của biến cố "tích các số trên hai thẻ rút ra là số chẵn" là:
3 : 6 = \(\dfrac{1}{2}\)
Kết luận:...
Cách thứ hai: Số cách chọn 2 thẻ bất kì (có kể thứ tự) là \(4.3=12\) cách. Như vậy, số cách chọn 2 thẻ không tính thứ tự là \(\dfrac{12}{2}=6\) cách.
Ta xét biến cố A: "Tích 2 số trên 2 thẻ rút ra là số chẵn." Biến cố đối của nó là \(\overline{A}\): "Tích 2 số trên 2 thẻ rút ra là số lẻ." Biến cố này tương đương với biến cố: "Cả 2 số trên 2 thẻ rút được là số lẻ."
Ta thấy trường hợp duy nhất thỏa mãn là rút được 2 tấm thẻ số 5 và 7. \(\Rightarrow P\left(\overline{A}\right)=\dfrac{1}{6}\) \(\Rightarrow P\left(A\right)=\dfrac{5}{6}\)
Vậy xác suất của biến cố: "Tích các số trên 2 thẻ rút ra là số chẵn." là \(\dfrac{5}{6}\).
một hộp chứa 4 cái thẻ cùng loại mỗi cái thẻ đc ghi một trong các số 1;2;3;4.Hai thẻ khác nhau thì ghi hai số khác nhau . Rút ngẫu nhiên hai thẻ trong hộp . Tính xác xuất của biến cố''Tích các số trên hai thẻ rút ra là số chẵn
Số cách rút ngẫu nhiên 2 thẻ khác nhau trong hộp là:
\(A^2_4=12\left(cách\right)\)
TH1: hai thẻ rút ra đều là số chẵn
Thẻ đầu tiên có 2 cách rút
Thẻ thứ hai có 1 cách rút
=>Có 2*1=2 cách rút
TH2: Trong hai thẻ rút ra có 1 thẻ chẵn, 1 thẻ lẻ
Số cách rút ra 1 thẻ chẵn là 2 cách
Số cách rút ra 2 thẻ chẵn là 2 cách
=>Có 2*2=4 cách rút
Tổng số cách để tích hai thẻ rút ra là số chẵn là:
2+4=6(cách)
Xác suất để rút ra hai thẻ có tích là số chẵn là:
\(\dfrac{6}{12}=\dfrac{1}{2}\)
Một hộp có 10 chiếc thẻ cùng loại , mỗi thẻ được ghi một trong các số 1, 2, 3,..., 10; hai thẻ khác nhau thì ghi hai số khác nhau.
Rút ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ rút được và bỏ lại thẻ đó vào hộp. Sau 25 rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
Tính xác suất thực nghiệm:
a) Xuất hiện số 1;
b) Xuất hiện số 5;
c) Xuất hiện số 10.
Một chiếc hộp có năm thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5, hai thẻ khác nhau thì ghi hai số khác nhau.

Rút ngẫu nhiên một chiếc thẻ trong hộp. Ghi lại số trên thẻ rút được và bỏ lại thẻ vào hộp. Sau 10 lần rút thẻ liên tiếp, bạn Hà Linh có kết quả thống kê như sau:
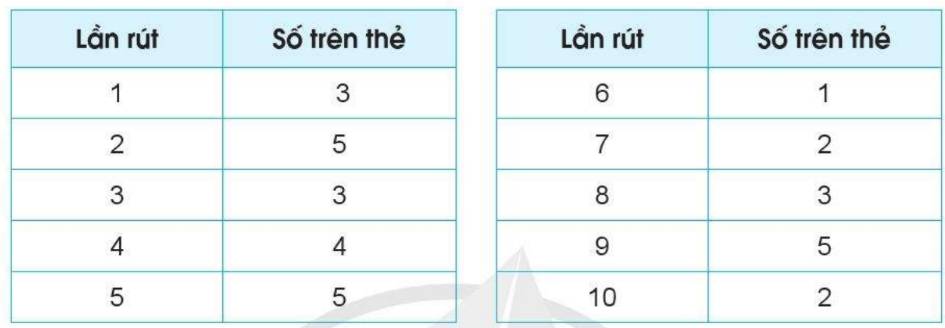
Hãy kiểm đếm số lần xuất hiện thẻ số 3 và thẻ số 5 sau 10 lần rút ngẫu nhiên.
Số lần xuất hiện thẻ số 3 là: 3 lần
Số lần xuất hiện thẻ số 5 là: 3 lần
Một hộp có 52 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, …, 51, 52; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biến cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1”.
b) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5”.
Tập hợp gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ rút ra là: B = {1, 2, 3, …, 51, 52}.
Số phần tử của B là 52.
a) Trong các số từ 1 đến 52 có ba số chia 17 dư 2 là: 2, 19, 36. Trong 3 số trên, có một số chia 3 dư 1 là 19.
Vậy có một kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số chia cho 17 dư 2 và chia cho 3 dư 1” là: 19.
Vì thế, xác suất của biến cố trên là: \(\dfrac{1}{{52}}\)
b) Có tám kết quả thuận lợi cho biến cố “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5” là: 5, 15, 25, 35, 45, 50, 51, 52.
Vì thế, xác suất của biến cố trên là: \(\dfrac{8}{{52}} = \dfrac{2}{{13}}\)
Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1; 2; …; 10. Hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp.
a. Viết tập hợp A kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra
b. Viết tập hợp B các kết quả thuận lợi cho biến cố “số xuất hiện trên thẻ được rút ra là số nguyên tố”.
c. Tính xác suất cho biến cố “số xuất hiện trên thẻ được rút ra là số nguyên tố”.
a: A={1;2;3;...;10}
b: B={2;3;5;7}
=>P(B)=4/10=2/5
Một hộp có 12 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3,…, 12; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Xét biến cố “Số xuất hiện trên thẻ được rút ra1 số là hợp số”. Tính xác suất của biến cố trên
n(omega)=12
A={4;6;9;10;12}
=>n(A)=5
=>P(A)=5/12
Một hộp có 50 chiếc thể cùng loại, mỗi thẻ được ghi một trong các số 1; 2; 3; 4; ...; 49; 50; hai thẻ khác nhau thì ghi hai số khác nhau. Rút ngẫu nhiên một thẻ trong hộp. Tính xác suất của mỗi biển cố sau:
a) “Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5".
b) “Số xuất hiện trên thẻ được rút ra là ước của 50".
c) “Số xuất hiện trên thẻ được rút ra là bội của 10".
d) “Số xuất hiện trên thẻ được rút ra là số lớn hơn 30".
a: Tập hợp các kết quả có thể xảy ra là \(\Omega=\left\{1;2;3;4;...;49;50\right\}\)
=>\(n\left(\Omega\right)=50\)
Gọi A là biến cố:"Số xuất hiện trên thẻ được rút ra là số có chứa chữ số 5"
=>A={5;15;25;35;45;50}
=>n(A)=6
=>\(P\left(A\right)=\dfrac{6}{50}=\dfrac{3}{25}\)
b: Gọi B là biến cố:“Số xuất hiện trên thẻ được rút ra là ước của 50"
=>B={1;2;5;10;25;50}
=>n(B)=6
\(P\left(B\right)=\dfrac{6}{50}=\dfrac{3}{25}\)
c: Gọi C là biến cố: "Số xuất hiện trên thẻ được rút ra là bội của 10"
Các bội của 10 trong tập hợp A là 10;20;30;40;50
=>C={10;20;30;40;50}
=>n(C)=5
=>\(P\left(C\right)=\dfrac{5}{50}=\dfrac{1}{10}\)
d: Gọi D là biến cố:"Số xuất hiện trên thẻ được rút ra là số lớn hơn 30"
Các số lớn hơn 30 trong tập hợp A là: 31;32;...;49;50
=>n(D)=20
=>\(P\left(D\right)=\dfrac{20}{50}=\dfrac{2}{5}\)
Một hộp có 10 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số nguyên dương không vượt quá 10, hai thẻ khác nhau thì ghi hai số khác nhau. Lấy ngẫu nhiên một chiếc thẻ từ trong hộp, ghi lại số của thẻ lấy ra và bỏ lại thẻ đó vào hộp. Sau 25 lần lấy thẻ liên tiếp, thẻ ghi số 5 được lấy ra 5 lần.
a) Tính xác suất thực nghiệm của biến cố “Thẻ lấy ra ghi số 5” trong trò chơi trên.
b) Nêu mối liên hệ giữa xác suất thực nghiệm của biến cố “Thẻ rút ra ghi số nguyên tổ” với xác suất của biến cố đó khi số lần rút thẻ ngày càng lớn.