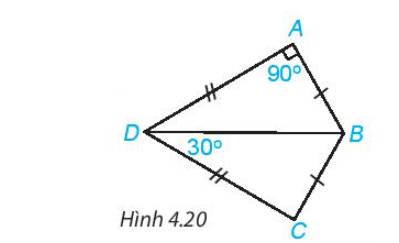
tính ABC
Những câu hỏi liên quan
Bài 10:Cho ABC có a 8, b 10, c 13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC Bài 11:Cho tam giác ABC có: a 6, b 7, c 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.Bài 12:Cho tam giác ABC có: AB 6, BC 7, AC 8. M trên cạnh AB sao cho MA 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.Bài 13:Cho ABC có 0 0 A B b 60 , 45 , 2...
Đọc tiếp
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
Cho góc ABC=56độ ABC' kề bù với gó ABC góc C'BA' kề bù vói góc ABC'.
a, Tính góc ABC'
b, Tính góc C'BA'
a) Ta có: \(\widehat{ABC'}\)kề bù với\(\widehat{ABC}\Rightarrow\widehat{ABC}+\widehat{ABC'}=180^o\Rightarrow56^o+\widehat{ABC'}=180^o=\widehat{ABC'}=124^o\)
b) Ta có: \(\widehat{C'BA'}\)kề bù với\(\widehat{ABC'}\Rightarrow\widehat{ABC'}+\widehat{C'BA'}=180^o\Rightarrow\widehat{ABC'}+\widehat{C'BA'}=180^o\Rightarrow24^o+\widehat{C'BA'}=180^o\Rightarrow\widehat{C'BA'}=56^o\)
Cho tam giác ABC có AB=8, AC=10,BC=13 A. TÍNH GÓC A B. TÍNH BÁN KÍNH đường tròn nội tiếp tam giác ABC. Tính diện tích tam giác ABC
Xem chi tiết
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=-\dfrac{1}{32}\)
\(\Rightarrow A\approx92^0\)
\(p=\dfrac{AB+AC+BC}{2}=\dfrac{31}{2}\)
\(S_{ABC}=\sqrt{p\left(p-AB\right)\left(p-AC\right)\left(p-BC\right)}\simeq40\)
\(r=\dfrac{S}{p}=\dfrac{80}{31}\)
Đúng 1
Bình luận (0)
Cho ABC có Aˆ= 300, Bˆ= 750, BC = 8cm.a. Tính AB b. Tính AC c. Tính diện tích ABC
Cho tam giác ABC có a=48cm,b=26cm,c=30cm
a) Tính các góc tam giác ABC
b)Tính diện tích tam giác ABC
c) Tính độ dài 3 đường trung tuyến của tam giác ABC
Cho tam giác ABC vuông tại Bcó AB 17cm, 067C. Tính ACCho tam giác ABC vuông tại Bcó AB 17cm, 067C. Tính AC.Cho tam giác ABC vuông tại Bcó AB 17cm, 067C. Tính AC.
Đọc tiếp
Cho tam giác ABC vuông tại Bcó AB= 17cm, 067C. Tính AC
Cho tam giác ABC vuông tại Bcó AB= 17cm, 067C. Tính AC.
Cho tam giác ABC vuông tại Bcó AB= 17cm, 067C. Tính AC.
\(sinC=\dfrac{AB}{AC}\Rightarrow AC=AB:sinC=17:sin67^0\simeq18,5\left(m\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC, AB=9cm, đường cao AH = 6 cm, sin ABC=4/5(Hình vẽ)
a, Tính BH, góc ABC( làm tròn đến phút)
b, tính AC,CH
c, Tính góc B, góc CAH
sin ABC=4/5
=>AH/AB=4/5
mà AH/AB=2/3
nên đề sai rồi bạn
Đúng 0
Bình luận (0)
a) biết tam giác abc = acb =bca. tính các góc tam giác abc
b) cho abc có góc a = 80 độ biết abc = acb. tính b , c
Vì các góc đều bằng nhau nên các góc đều bằng: 180o:3=60o
Hay còn gọi ABC là tam giác cân
Đúng 0
Bình luận (0)
cho hc S.ABC với đáy ABC vuông B , AB=a, SA vuông đáy và SA=a\(\sqrt{3}\) BC=2a
a) xđ và tính góc (SC,(ABC))
b) xđ và tính góc ((SBC),(ABC)
C) tính d(A,(SBC))
2 cho hc S.ABCD đáy là hình vuông cạnh a SA vuông đáy SA=3a
a) xđ và tính góc (SB, (ABC))
b) xđ và tính góc (SBC),(ABC))
c) d(A,(SBC))
1.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SA lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC là (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{5}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=\dfrac{\sqrt{15}}{5}\Rightarrow\widehat{SCA}\approx37^045'\)
b.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABC\right)\\SB=\left(SBC\right)\cap\left(SAB\right)\\AB=\left(ABC\right)\cap\left(SAB\right)\end{matrix}\right.\) \(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{3}\Rightarrow\widehat{SBA}=60^0\)
c.
Trong mp (SAB), từ A kẻ \(AH\perp SB\)
Mà \(BC\perp\left(SAB\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{3}}{2}\)
Đúng 1
Bình luận (0)
2.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB là (ABCD)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=3\Rightarrow\widehat{SBA}\approx71^034'\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Mà \(\left\{{}\begin{matrix}BC=\left(SBC\right)\cap\left(ABCD\right)\\SB=\left(SAB\right)\cap\left(SBC\right)\\AB=\left(SAB\right)\cap\left(ABCD\right)\end{matrix}\right.\)
\(\Rightarrow\widehat{SBA}\) là góc giữa (SBC) và (ABCD) (đã tính ở câu a)
c.
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{3a\sqrt{10}}{10}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông góc tại A có AB=3cm; BC= 5cm. Vẽ đường AH của tam giác ABC
a. Chứng minh tam giác ABC động dạng với tam giác HAC
b. Tính AH, AC
c. Đường phân giác BD của tam giác ABC cắt AH ở E. Tính EH/EA. Tính EH
d. Tính diện tích tứ giác HEDC
