Question

tính ABC

Answer 1

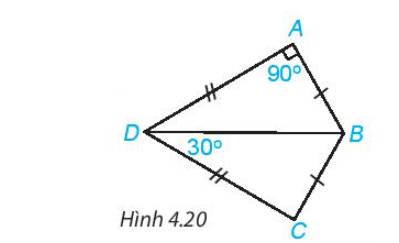
Xét \(\Delta ABD\) và \(\Delta CBD\) ta có:

\(AB=BC\left(gt\right)\)

\(AD=CD\left(gt\right)\)

\(DB\) chung 

\(\Rightarrow\Delta ABD=\Delta CBD\left(c.c.c\right)\) 

\(\Rightarrow\widehat{BDC}=\widehat{ADB}=30^o\) 

Xét ΔABD có:

\(\widehat{ABD}=180^o-30^o-90^o=60^o\)

\(\Rightarrow\widehat{ABD}=\widehat{CBD}=60^o\)

\(\Rightarrow\widehat{ABC}=\widehat{ABD}+\widehat{CBD}=60^o+60^o=120^o\)

Answer 2

ΔCBD vuông tại C

=>góc CDB+góc CBD=90 độ

=>góc CBD=90-30=60 độ

Xét ΔADB và ΔCDB có

AD=CD

DB chung

AB=CB

Do đó: ΔADB=ΔCDB

=>góc ABD=góc CBD

=>góc ABC=2*góc CBD=120 độ