viết tập hơp các số tự nhiên có 4 chữ số chia hết cho 10 được lập bởi các số 0,2,3,5

Những câu hỏi liên quan
Cho tập X={1;2;3...;8}. Lập từ X số tự nhiên có 8 chữ số đôi một khác nhau. Xác suất để lập được số chia hết cho 1111 là?
Cho tập hơp X gồm các số TN có 6 chữ số đôi một khác nhau có dạng abcdef. Từ X lấy ngẫu nhiên một số. Tính xs để số lấy ra là số lẻ và t/m a<b<c<d<e<f
Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Đúng 2
Bình luận (0)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số
Đúng 1
Bình luận (0)
1.Cho các số 0,2,3,5.Hỏi lập được tất cả bao nhiêu số tự nhiên có 4 chữ số khác nhau từ các chữ số trên?
Lập được 18 số khác nhau từ những số trên đó là :
2035 3025 5023
2053 3052 5032
2305 3205 5203
2350 3250 5230
2503 3502 5302
2530 3520 5320
Đúng 0
Bình luận (0)
một số viết thành 6 số ngoài số 0 thì viết được 6 * 3 = 16 số nhé bạn
Đúng 1
Bình luận (0)
làm cách chọn đc ko bn?Mà bn giải rõ ra cho mik nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tập hợp . Gọi là tập hợp các số tự nhiên có 4 chữ số lập từ các chữ số thuộc tập . Chọn ngẫu nhiên một số từ , xác suất để số được chọn chia hết cho bằng A.
9
28
B.
4
27
C.
4
9
D.
1
9
Đọc tiếp
Cho tập hợp . Gọi là tập hợp các số tự nhiên có 4 chữ số lập từ các chữ số thuộc tập . Chọn ngẫu nhiên một số từ , xác suất để số được chọn chia hết cho bằng
A. 9 28
B. 4 27
C. 4 9
D. 1 9
số tự nhiên bé nhất có 4 chữ số được viết bởi các chữ số 2,0,1.9 mà chia hết cho 3 là:
Để được số bé nhất thì số ở hàng càng cao thì càng nhỏ.
Số bé nhất có 4 chữ số mà chia hết cho 3 được lập từ các chữ số :
2; 0; 1; 9 là: 1029
Đúng 2
Bình luận (0)
Cho tập hợp
A
1
;
2
;
3
;
4
;
5
;
6
;
7
;
8
;
9
. Gọi S là tập hợp các số tự nhiên có 4 chữ số được lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng A. ...
Đọc tiếp
Cho tập hợp A = 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 ; 8 ; 9 . Gọi S là tập hợp các số tự nhiên có 4 chữ số được lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng
A. 1 9
B. 4 9
C. 4 27
D. 9 28
Tập S có 9 4 phần tử. Ta có
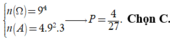
Thật vậy: Gọi số thỏa mãn biến cố là ![]()
Đúng 0
Bình luận (0)
cho các số 0,2,3,5. Hỏi lập được tất cả bao nhiêu số tự nhiên khác nhau mà có đủ mặt 4 chữ số đã cho
12 số nha  I can rest your love on me
I can rest your love on me
Đúng 0
Bình luận (0)
Có 3 cách chọn chữ số hàng nghìn
Có 3 cách chọn chữ số hàng trăm
Có 2 cách chọn chữ số hàng chục
Có 1 cách chọn chữ số hàng đơn vị
có tất cả số thỏa mãn đề bài là:
3x3x2x1=18 (số)
Đáp số: 18 số
Đúng 0
Bình luận (0)
Có 3 cách chọn chữ số hàng nghìn
Có 3 cách chọn chữ số hàng trăm
Có 2 cách chọn chữ số hàng chục
Có 1 cách chọn chữ số hàng đơn vị
Có tất cả:3x3x2x1=18(số)
duyệt đi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tập hợp A{1;2;3;4;5;6;7;8;9}. Gọi S là tập hợp các số tự nhiên có 4 chữ số lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng A.
9
28
B.
4
27
C.
4
9
D.
1
9
Đọc tiếp
Cho tập hợp A={1;2;3;4;5;6;7;8;9}. Gọi S là tập hợp các số tự nhiên có 4 chữ số lập từ các chữ số thuộc tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn chia hết cho 6 bằng
A. 9 28
B. 4 27
C. 4 9
D. 1 9
Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
A
.
1
63
B
.
8
21
C
.
1
84
D
.
...
Đọc tiếp
Cho A là tập tất cả các số tự nhiên có 4 chữ số phân biệt được lập từ tập {1;2;3;4;5;6;7;8;9}. Chọn ngẫu nhiên một số từ tập A. Xác suất để chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11 bằng
A . 1 63
B . 8 21
C . 1 84
D . 1 42
Chọn A
Số phần tử của A là A 9 4 = 3024 số.
Số phần tử của không gian mẫu là n ( Ω ) = 3024
Gọi A là biến cố: “Chọn được một số chia hết cho 11 và tổng bốn chữ số của nó chia hết cho 11”.
Xét số tự nhiên có 4 chữ số có dạng ![]()
Theo bài ra ta có: ![]() và
và ![]()
Suy ra ![]()
Trong các chữ số 1;2;3;4;5;6;7;8;9 có các bộ số mà tổng chia hết cho 11 là ![]()
Chọn 2 cặp trong 4 cặp số trên để tạo số ![]()
Chọn {a;c} có 4 cách, chọn {b;d} có 3 cách, sau đó sắp thứ tự các số a, b, c, d. Ta được 4.3.2.2 = 48
Suy ra n(A) = 48
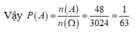
Đúng 0
Bình luận (0)
có bao nhiêu số tự nhiên có 4 chữ số được lập bởi các chữ số 1,2,3 biết rằng số đó chia hết cho 9
chia hết cho 9: tổng các chữ số chia hết cho 9
=> Chỉ có 2 bộ số:
1 chữ số 3: {3,2,2,2}
2 chữ số 3: {3,3,1,2}
TH1: có 4 cách đặt vị trí cho số 3. (Có 4 số)
TH2: có 4 cách đặt vị trí cho số 1, với mỗi cách đó có 3 cách đặt vị trí cho số 2 (có 4 x 3 = 12 số)
=> CÓ 4 + 12 = 16 số
Đúng 0
Bình luận (0)
có 16 số
mk chỉ suy đoán thôi ! nếu đúng thì tk mk nha !
Đúng 0
Bình luận (0)

























