Tìm một số hình ảnh về hai đường thẳng vuông góc ở xung quanh em

Những câu hỏi liên quan
Tìm một số hình ảnh về hai đường thẳng song song ở xung quanh em.
Một số hình ảnh về hai đường thẳng song song ở xung quanh em: Hai cây đũa khi xếp cạnh nhau, hai mép của quyển sách…
Đúng 0
Bình luận (0)
Tìm hình ảnh các đường thẳng vuông góc, các đường thẳng song song xung quanh em.

Em hãy tìm một số hình ảnh về góc nhọn, góc tù, góc vuông có ở những đồ vật quanh em như: bàn ghế, ê ke, com pa,...
+ Hình ảnh hai kim đồng hồ lúc 8 giờ cho ta hình ảnh về góc tù.

+ Hình ảnh góc tường nhà cho ta hình ảnh về góc vuông

Đúng 1
Bình luận (0)
quan sát xung quanh và chỉ ra hình ảnh của các đường thẳng song song hay các đường thẳng vuông góc với nhau
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 độ. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh
S
x
q
của hình nón (N). A.
27
3
π
B.
18
3
π
C...
Đọc tiếp
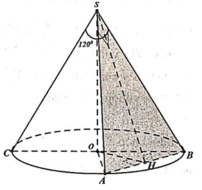
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 độ. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh S x q của hình nón (N).
A. 27 3 π
B. 18 3 π
C. 9 3 π
D. 36 3 π
Hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120°. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3. Tính diện tích xung quanh Sxq của hình nón (N). A.
36
3
π
B.
27
3
π
C.
18
3
π
D.
9...
Đọc tiếp
Hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120°. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3. Tính diện tích xung quanh Sxq của hình nón (N).
A. 36 3 π
B. 27 3 π
C. 18 3 π
D. 9 3 π
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng
120
0
.
Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh
S
x
q
của hình nón
N
.
A.
S
x
q...
Đọc tiếp
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 0 . Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh S x q của hình nón N .
A. S x q = 36 3 π .
B. S x q = 27 3 π .
C. S x q = 18 3 π .
D. S x q = 9 3 π .
Đáp án C.
Phương pháp:
Diện tích xung quanh của hình nón: S x q = π R l
Cách giải:
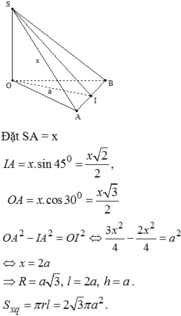
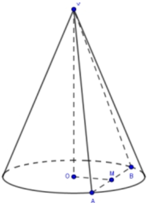
Gọi M là trung điểm AB ⇒ O M ⊥ A B . Mà O M ⊥ S O (vì SO vuông góc với đáy)
⇒ OM là đoạn vuông góc chung của SO và AB
⇒ d S O ; A B = O M = 3
Tam giác OMA vuông tại M:
O A 2 = O M 2 + M A 2 ⇒ R 2 = 3 2 + M A 2 ⇒ M A = R 2 − 9
Tam giác SAB vuông tại A có S A = S B (Vì Δ S O B = Δ S O A c . g . c )
⇒ Δ S A B vuông cân tại S
⇒ S A = A B 2 = 2 A M 2 = A M . 2 = 3 R 2 − 18
(N) có góc ở đỉnh là
120 0 ⇒ A S O = 60 0
Tam giác SOA vuông tại O:
sin O S A = O A S A ⇒ sin 60 0 = R 3 R 2 − 18 = 3 2 ⇒ 2 R = 3 . 3 R 2 − 18 ⇔ 4 R 2 = 6 R 2 − 54
⇔ R 2 = 27 ⇒ R = 3 3 .
l = S A = 2 R 2 − 18 = 2.27 − 18 = 36 = 6
S x q = π R l = π .3 3 .6 = 18 π 3
Đúng 0
Bình luận (0)
Tìm trong thực tế hình ảnh các loại góc đã học và hình ảnh hai đường thẳng vuông góc, hai đường song song.

Tham khảo:
Hình ảnh về góc:

Hình ảnh về hai đường thẳng vuông góc:

Hình ảnh về hai đường thẳng song song:

Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD. Một góc vuông xAy quay xung quanh đỉnh A. Tia Ax cắt BC ở E và tia AY cắt CD ở F. Gọi G là đỉnh thứ tư của hình chữ nhật AEGF.
a) Tìm tập hợp tâm O của hình chữ nhật AEGF khi góc vuông xAy quay xung quanh quanh đỉnh A
b) Tìm tập hợp đỉnh G của hình chữ nhật AEGF