Các câu hỏi tương tự
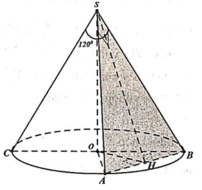
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 độ. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh
S
x
q
của hình nón (N). A.
27
3
π
B.
18
3
π
C...
Đọc tiếp
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 độ. Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh S x q của hình nón (N).
A. 27 3 π
B. 18 3 π
C. 9 3 π
D. 36 3 π
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng
120
0
.
Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh
S
x
q
của hình nón
N
.
A.
S
x
q...
Đọc tiếp
Cho hình nón (N) có đỉnh S, tâm đường tròn đáy là O, góc ở đỉnh bằng 120 0 . Một mặt phẳng qua S cắt hình nón (N) theo thiết diện là tam giác vuông SAB. Biết rằng khoảng cách giữa hai đường thẳng AB và SO bằng 3, tính diện tích xung quanh S x q của hình nón N .
A. S x q = 36 3 π .
B. S x q = 27 3 π .
C. S x q = 18 3 π .
D. S x q = 9 3 π .
Cho hình nón đỉnh
S
, đáy là hình tròn tâm
O
. Thiết diện qua trục của hình nón là tam giác có một góc bằng
120
0
, thiết diện qua đỉnh
S
cắt mặt phẳng đáy theo dây cung
A
B
4
a
và là một tam giác vuông. Diện tích xung quanh của hình nón bằng A.
π
3
a
2
. B....
Đọc tiếp
Cho hình nón đỉnh S , đáy là hình tròn tâm O . Thiết diện qua trục của hình nón là tam giác có một góc bằng 120 0 , thiết diện qua đỉnh S cắt mặt phẳng đáy theo dây cung A B = 4 a và là một tam giác vuông. Diện tích xung quanh của hình nón bằng
A. π 3 a 2 .
B. π 8 3 a 2 .
C. π 2 3 a 2 .
D. π 4 3 a 2 .
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R3cm, góc ở đỉnh hình nón là
α
120
°
. Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng A.
3
3
c
m
2
B.
6
3
c
m...
Đọc tiếp
Cho hình nón đỉnh S, đáy là hình tròn tâm O, bán kính R=3cm, góc ở đỉnh hình nón là α = 120 ° . Cắt hình nón bởi mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A, B thuộc đường tròn đáy. Diện tích tam giác SAB bằng
A. 3 3 c m 2
B. 6 3 c m 2
C. 6 c m 2
D. 3 c m 2
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính
R
3
c
m
,
góc ở đỉnh của hình nón là
φ
120
0.
.
Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng A.
3
3
c
m
2
.
B....
Đọc tiếp
Cho hình nón có đỉnh S, đáy là hình tròn tâm O, bán kính R = 3 c m , góc ở đỉnh của hình nón là φ = 120 0. . Cắt hình nón bởi một mặt phẳng qua đỉnh S tạo thành tam giác đều SAB, trong đó A,B thuộc đường tròn đáy. Diện tích của tam giác SAB bằng
A. 3 3 c m 2 .
B. 6 3 c m 2 .
C. 6 c m 2 .
D. 3 c m 2 .
Một hình nón tròn xoay có bán kính bằng chiều cao và bằng 1. Gọi O là tâm của đường tròn đáy. Xét thiết diện qua đỉnh S hình nón là tam giác đều SAB. Tính khoảng cách từ O đến mặt phẳng ( SAC ) A.
3
B.
3
3
C. 2
3
D.
2
3
3
Đọc tiếp
Một hình nón tròn xoay có bán kính bằng chiều cao và bằng 1. Gọi O là tâm của đường tròn đáy. Xét thiết diện qua đỉnh S hình nón là tam giác đều SAB. Tính khoảng cách từ O đến mặt phẳng ( SAC )
A. 3
B. 3 3
C. 2 3
D. 2 3 3
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng
A
B
a
,
A
C
a
3
, đường thẳng SA tạo với đáy một góc
60
°
. Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi
S
x
q
là diện tích...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A, hình chiếu vuông góc của đỉnh S trên đáy là trung điểm O của cạnh BC. Biết rằng A B = a , A C = a 3 , đường thẳng SA tạo với đáy một góc 60 ° . Một hình nón có đỉnh là S, đường tròn đáy ngoại tiếp tam giác ABC. Gọi S x q là diện tích xung quanh của hình nón. Tính S x q
A. S x q = 4 πa 2 3 3
B. S x q = 4 πa 2
C. S x q = 2 πa 2 3 3
D. S x q = 2 πa 2
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O bằng bao nhiêu, biết rằng thể tích của nó bằng
1
8
thể tích khối nón đỉnh S, đáy là hình tròn tâm O. A. h 5 B. h 10 C. h 20 D. h 40
Đọc tiếp
Cho hình nón đỉnh S, đáy là hình tròn tâm O và có chiều cao bằng 40. Cắt hình nón bằng một mặt phẳng song song với mặt phẳng đáy, thiết diện thu được là đường tròn tâm O'. Chiều cao h của khối nón đỉnh S đáy là hình tròn tâm O' bằng bao nhiêu, biết rằng thể tích của nó bằng 1 8 thể tích khối nón đỉnh S, đáy là hình tròn tâm O.
A. h = 5
B. h = 10
C. h = 20
D. h= 40
Một hình nón có đỉnh S, đường cao SO, gọi A, B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ AB đến O bằng a và góc
S
A
O
^
30
°
,
S
A
B
^
60
°
. Tính diện tích xung quanh nón. A.
S
x
q...
Đọc tiếp
Một hình nón có đỉnh S, đường cao SO, gọi A, B là hai điểm thuộc đường tròn đáy sao cho khoảng cách từ AB đến O bằng a và góc S A O ^ = 30 ° , S A B ^ = 60 ° . Tính diện tích xung quanh nón.
A. S x q = 2 πa 2 3
B. S x q = 3 πa 2 3
C. S x q = πa 2 3
D. S x q = 4 πa 2 3