Cho đồ thị của hàm số \(y = {\log _2}x\) và y = 2 như Hình 6.8. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {\log _2}x\) nằm phía trên đường thẳng y = 2 và từ đó suy ra tập nghiệm của bất phương trình \({\log _2}x > 2.\)

Cho đồ thị của hàm số \(y = {2^x}\) và \(y = 4\) như Hình 6.7. Tìm khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 và từ đó suy ra tập nghiệm của bất phương trình \({2^x} > 4.\)

Khoảng giá trị của x mà đồ thị hàm số \(y = {2^x}\) nằm phía trên đường thẳng y = 4 là \(\left( {2; + \infty } \right)\)
Vậy tập nghiệm của bất phương trình \({2^x} > 4\) là \(\left( {2; + \infty } \right)\)
a) Vẽ đồ thị hàm số \(y = {\log _4}x\) và đường thẳng y = 5
b) Nhận xét về số giao điểm của hai đồ thị trên. Từ đó, hãy nêu nhận xét về số nghiệm của phương trình \({\log _4}x = 5\)
a:
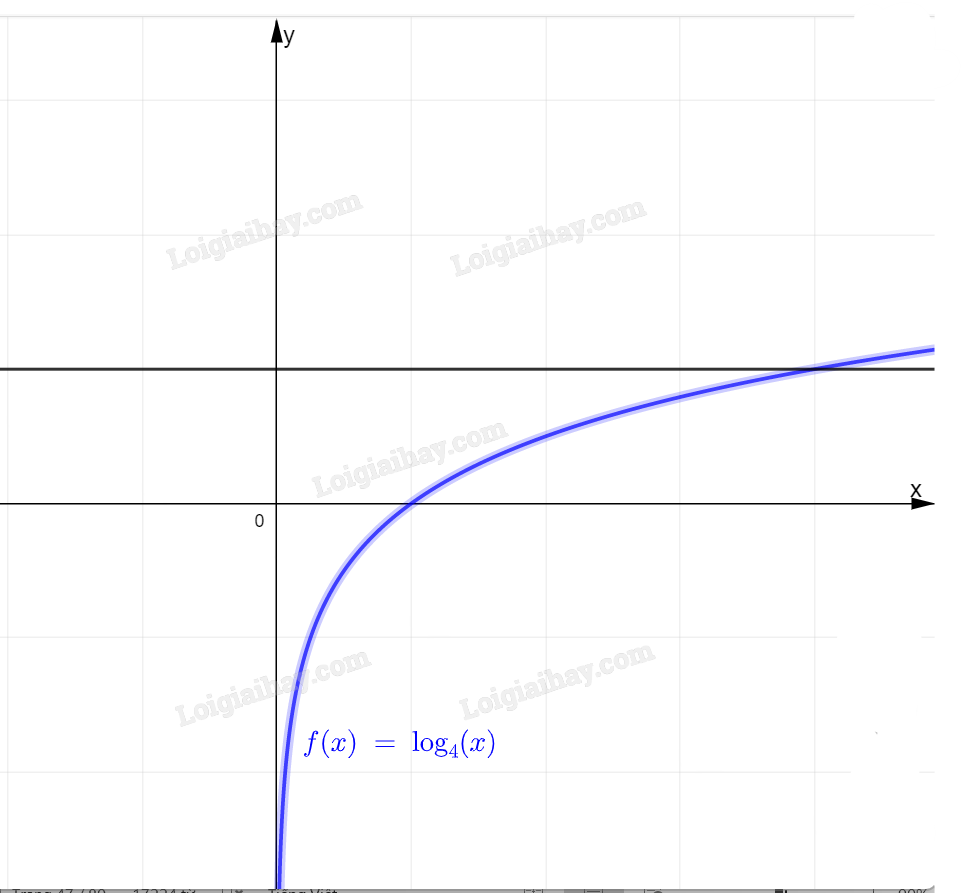
b: Hai đồ thị này có 1 giao điểm
=>Phương trình \(log_4x=5\) có 1 nghiệm duy nhất
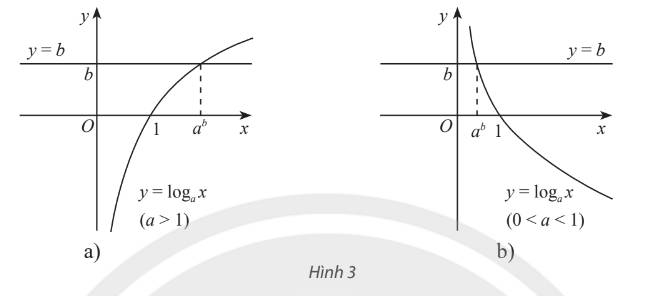
Cho đồ thị của hai hàm số \(y = {\log _a}x\left( {a > 0,a \ne 1} \right)\) và \(y = b\) như Hình 3a (với \(a > 1\)) hay Hình 3b (với \(0 < a < 1\)). Từ đây hãy nhận xét về số nghiệm và công thức nghiệm của phương trình \({\log _a}x = b\).
tham khảo.
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).
Hoạt động 6
Quan sát Hình 12 và nêu nhận xét về tính đồng biến, nghịch biến của hàm số lôgarit \(y = {\log _2}x\). Từ đó, hãy tìm x sao cho \({\log _2}x > 1\)
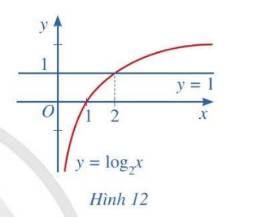
Do 2 > 1 ⇒ hàm số y = log2x đồng biến trên D = \(\left(0;+\infty\right)\)
\(log_2x>1\\ \Rightarrow x>2\)
Cho hàm số y=f(x) có đạo hàm liên tục trên tập R/ 2 và có đồ thị hàm số y=f’(x) như hình vẽ. Biết f 1 ≠ 10 f(3)=4 . Có bao nhiêu tiếp tuyến của đồ thị hàm số mà tiếp tuyến đó song song với đường thẳng 3x+y-13
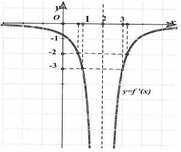
A. 2
B. 1
C. 0.
D. 3
Cho hàm số y = x\(^2\) có đồ thị (P\(_1\)) và hàm số y = -x\(^2\) có đồ thị (P\(_2\))
a) Vẽ đồ thị của các hàm số này trên cùng một mặt phẳng tọa độ.
b) Gọi A là một điểm bất kì trên (P\(_1\)) và B là điểm đối xứng với A qua trục hoành. Chứng minh rằng điểm B nằm trên (P\(_2\)).
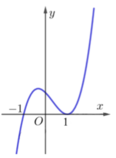
Cho hàm số y=f(x)(x-1) xác định và liên tục trên R và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = m 2 - m cắt đồ thị hàm số f x x - 1 tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
A. m > 0
B. [ m > 1 m < 0
C. m < 1
D. 0 < m < 1
Đáp án B
Lấy đối xứng đồ thị hàm số f(x)(x-1) qua trục Ox ta được đồ thị của hàm số f x x - 1 . Từ đồ thị hàm số f x x - 1 ta thấy đường thẳng y = m 2 - m cắt hàm số f x x - 1 tại 2 điểm nằm ngoài [-1;1]
⇔ m 2 - m > 0 ⇔ [ m < 0 m > 1
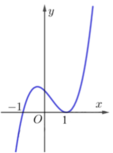
Cho hàm số y = f(x)(x - 1) xác định và liên tục trên ℝ và có đồ thị như hình vẽ dưới đây. Tìm tất cả các giá trị thực của tham số m để đường thẳng y = f x x − 1 cắt đồ thị hàm số tại 2 điểm có hoành độ nằm ngoài đoạn [-1;1]
A. m > 0.
B. m > 1 m < 0 .
C. m < 1.
D. 0 < m < 1.
Đáp án B
Lấy đối xứng đồ thị hàm số f ( x ) ( x − 1 ) qua trục Ox ta được đồ thị của hàm số f ( x ) x − 1 . Từ đồ thị hàm số f ( x ) x − 1 ta thấy đường thẳng y = m 2 − m cắt hàm số f ( x ) x − 1 tại 2 điểm nằm ngoài [ − 1 ; 1 ] ⇔ m 2 − m > 0 ⇔ m < 0 m > 1
Tìm tất cả các giá trị thực của x để đồ thị hàm số y = log0,5x nằm phía trên đường thẳng y = 2
![]()
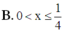
![]()
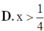
Đáp án C
Ta có log0,5x > 2 <=> 0 < x < 1 4