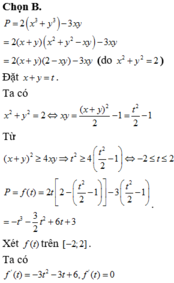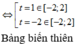Cho x + y = 1 tìm giá trị nhỏ nhất của biểu thức M = x3 + y3

Những câu hỏi liên quan
Cho x,y là số dương thỏa mãn x+y<1. Tìm giá trị nhỏ nhất của biểu thức: A= 1/x3+3xy2 + 1/y3+3x2y
Cho hai số x,y \(\ge\)0 thay đổi và thỏa mãn x+y=2. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P= x(x3 + x2 + x + 1004y) + y(y3 + y2 + y +1004x) + 1
Cho các số thực x,y thoả mãn x+y 2.Tìm giá trị nhỏ nhất của biểu thức: A x3�3 + y3�3 + x2�2 + y2
Đọc tiếp
Cho các số thực x,y thoả mãn x+y =2.Tìm giá trị nhỏ nhất của biểu thức: A= + + +
Lời giải:
$A=(x+y)(x^2-xy+y^2)+x^2+y^2=2(x^2-xy+y^2)+x^2+y^2=2(x^2+y^2)+(x-y)^2$
$\geq 2(x^2+y^2)=(1^2+1^2)(x^2+y^2)\geq (x+y)^2=2^2=4$ (theo BĐT Bunhiacopxky)
Vậy $A_{\min}=4$. Giá trị này đạt tại $x=y=1$
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của biểu thức
T
x
3
+
y
3
−
x
2
+
y
2
x
−...
Đọc tiếp
Tìm giá trị nhỏ nhất của biểu thức T = x 3 + y 3 − x 2 + y 2 x − 1 y − 1 với x, y là các số thực lớn hơn 1
Ta có: T = x 3 + y 3 − x 2 + y 2 x − 1 y − 1 = x 2 x − 1 + y 2 y − 1 x − 1 y − 1 = x 2 y − 1 + y 2 x − 1
Do x > 1 , y > 1 nên x − 1 > 0 , y − 1 > 0
Áp dụng bất đẳng thức Cauchy cho 2 số dương x 2 y − 1 , y 2 x − 1 ta có:
x − 1 + 1 ≥ 2 x − 1 ⇔ x − 1 − 1 2 ≥ 0 ⇔ x − 2 x − 1 ≥ 0 ⇔ x x − 1 ≥ 2 y − 1 + 1 ≥ 2 y − 1 ⇔ y − 1 − 1 2 ≥ 0 ⇔ y − 2 y − 1 ≥ 0 ⇔ x y − 1 ≥ 2
Do đó: T = x 2 y − 1 + y 2 x − 1 ≥ 2 x y x − 1 . y − 1 ≥ 8
Dấu “=” xẩy ra khi x 2 y − 1 = y 2 x − 1 x − 1 = 1 y − 1 = 1 ⇔ x = 2 y = 2 (thỏa mãn điều kiện)
Vậy giá trị nhỏ nhất của biểu thứcT= 8 khi x=y= 2
Đúng 0
Bình luận (0)
Cho hai số thực x, y thay đổi thỏa mãn điều kiện
x
2
+
y
2
2
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P
2
(
x
3
+
y
3
)
...
Đọc tiếp
Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. - 1 2
C. -6
D. 1 - 4 2
Chọn B.
P =
2
(
x
3
+
y
3
)
-
3
x
y
![]()
![]() (do
x
2
+
y
2
=
2
)
(do
x
2
+
y
2
=
2
)
Đặt x + y = t. Ta có
x
2
+
y
2
=
2
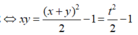
Từ ![]()
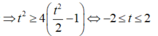
P = f(t) 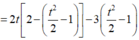
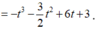
Xét f(t) trên [-2;2].
Ta có ![]()
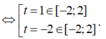
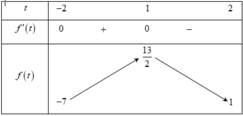
Bảng biến thiên
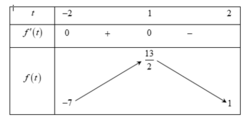
Từ bảng biến thiên ta có max P = max f(t) = 13 2 ; min P = min f(t) = -7
Lời bình: Có thể thay bbt thay bằng
Ta có ![]()
Suy ra kết luận.
Đúng 0
Bình luận (0)
Cho hai số thực x, y thay đổi thỏa mãn điều kiện
x
2
+
y
2
2
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức
P
2
(
x
3
+
y
3
)
-
3
x
y
. Giá trị của của M + m bằng A. -4 B. -...
Đọc tiếp
Cho hai số thực x, y thay đổi thỏa mãn điều kiện x 2 + y 2 = 2 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = 2 ( x 3 + y 3 ) - 3 x y . Giá trị của của M + m bằng
A. -4
B. -1/2
C. -6
D. 1
cho x+y=1 tìm giá trị nhỏ nhất M=x3+y3+2xy
Lời giải:
$M=x^3+y^3+2xy=(x+y)(x^2-xy+y^2)+2xy=x^2-xy+y^2+2xy$
$=x^2+y^2+xy=\frac{1}{4}(x-y)^2+\frac{3}{4}(x+y)^2=\frac{1}{4}(x-y)^2+\frac{3}{4}\geq \frac{3}{4}$
Vậy $M_{\min}=\frac{3}{4}$. Giá trị này đạt được khi $x=y=\frac{1}{2}$
Đúng 0
Bình luận (0)
Cho các số thực x,y thoả mãn x+y=2.Tìm giá trị nhỏ nhất của biểu thức:
A= x3 + y3 + 3x2y2
A=(x+y)3 - 3xy(x+y)+3x2y2
=8-6xy+3x2y2
=3(x2y2-2xy+1)+5
=3(xy+1)2+5 ≥5
dấu = xảy ra ⇔ xy=1 ⇒ x=y=1
Đúng 1
Bình luận (0)
a) Cho x + y = 1. Tính giá trị biểu thức A = x3 + y3 +3xy
b) Cho x - y = 1. Tính giá trị biểu thức B = x3 - y3 -3xy
a) \(A=x^3+y^3+3xy\)
\(=x^3+y^3+3xy\left(x+y\right)\) (do \(x+y=1\))
\(=x^3+3x^2y+3xy^2+y^3\)
\(=\left(x+y\right)^3\) \(=1\)
b) \(B=x^3-y^3-3xy\)
\(=x^3-y^3-3xy\left(x-y\right)\) (do \(x-y=1\))
\(=x^3-3x^2y+3xy^2-y^3\)
\(=\left(x-y\right)^3\) \(=1\)
Đúng 2
Bình luận (0)