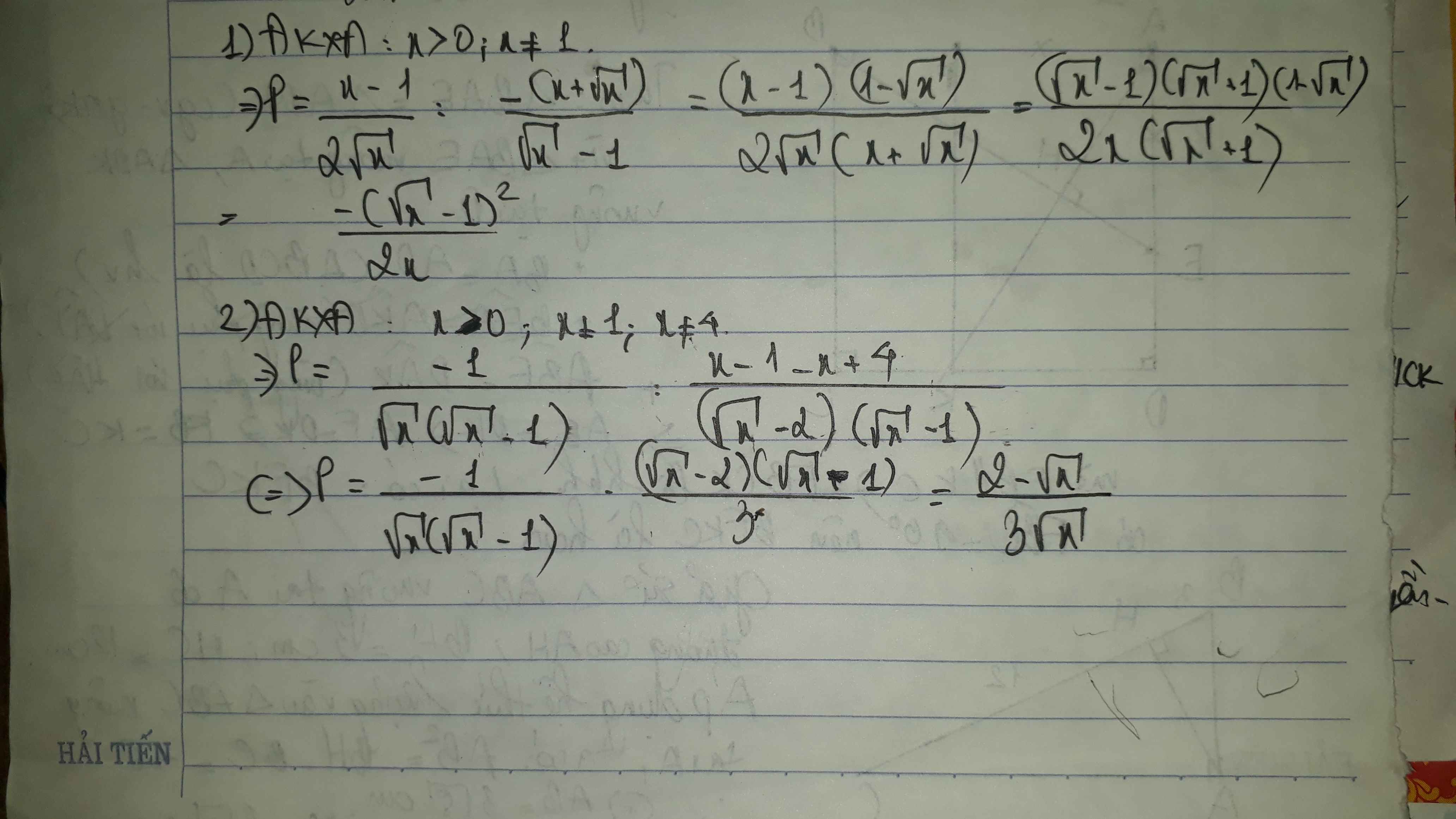\(1+\dfrac{\sqrt{\left(x-1\right)}}{x-1}\)

Những câu hỏi liên quan
left(dfrac{x+2}{xsqrt{x}-1}+dfrac{sqrt{x}}{x+sqrt{x}+1}+dfrac{1}{1-sqrt{x}}right):dfrac{sqrt{x}-1}{2}
left(dfrac{x+2}{left(sqrt{x}-1right)left(x+sqrt{x}+1right)}+dfrac{sqrt{x}left(sqrt{x}-1right)}{left(sqrt{x}-1right)left(x+sqrt{x}+1right)}-dfrac{1}{sqrt{x}-1}right).dfrac{2}{sqrt{x}-1}
dfrac{x+2+x-sqrt{x}-x-sqrt{x}-1}{left(sqrt{x}-1right)left(x+sqrt{x}+1right)}.dfrac{2}{sqrt{x}-1}dfrac{sqrt{x}-1}{x+sqrt{x}+1}.dfrac{2}{sqrt{x}-1}dfrac{2}{x+sqrt{x}+1}
Đọc tiếp
\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}-1}{2}\)
\(=\left(\dfrac{x+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}-1}\right).\dfrac{2}{\sqrt{x}-1}\)
= \(\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}.\dfrac{2}{\sqrt{x}-1}\)=\(\dfrac{\sqrt{x}-1}{x+\sqrt{x}+1}.\dfrac{2}{\sqrt{x}-1}=\dfrac{2}{x+\sqrt{x}+1}\)
Rút gọn:
M1-left[dfrac{2x-1+sqrt{x}}{1-x}+dfrac{2xsqrt{x}+x-sqrt{x}}{1+xsqrt{x}}right]cdotleft[dfrac{left(x-sqrt{x}right)left(1-sqrt{x}right)}{2sqrt{x}-1}right]
Giải::
ĐK: x khác +- 1
M1-left[dfrac{left(sqrt{x}-dfrac{1}{2}right)left(sqrt{x}+1right)}{left(1+sqrt{x}right)left(1-sqrt{x}right)}+dfrac{sqrt{x}left(sqrt{x}-dfrac{1}{2}right)left(sqrt{x}+1right)}{left(1+sqrt{x}right)left(1-sqrt{x}+xright)}right]cdotleft[dfrac{-sqrt{x}left(1-sqrt{x}right)^2}{2left(sqrt{x}-dfrac{1}{2}right)}right...
Đọc tiếp
Rút gọn:
\(M=1-\left[\dfrac{2x-1+\sqrt{x}}{1-x}+\dfrac{2x\sqrt{x}+x-\sqrt{x}}{1+x\sqrt{x}}\right]\cdot\left[\dfrac{\left(x-\sqrt{x}\right)\left(1-\sqrt{x}\right)}{2\sqrt{x}-1}\right]\)
Giải::
ĐK: x khác +- 1
\(M=1-\left[\dfrac{\left(\sqrt{x}-\dfrac{1}{2}\right)\left(\sqrt{x}+1\right)}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-\dfrac{1}{2}\right)\left(\sqrt{x}+1\right)}{\left(1+\sqrt{x}\right)\left(1-\sqrt{x}+x\right)}\right]\cdot\left[\dfrac{-\sqrt{x}\left(1-\sqrt{x}\right)^2}{2\left(\sqrt{x}-\dfrac{1}{2}\right)}\right]\)
\(=1-\left[\dfrac{\left(\sqrt{x}-\dfrac{1}{2}\right)}{\left(1-\sqrt{x}\right)}\cdot\dfrac{-\sqrt{x}\left(1-\sqrt{x}\right)^2}{2\left(\sqrt{x}-\dfrac{1}{2}\right)}+\dfrac{\sqrt{x}\left(\sqrt{x}-\dfrac{1}{2}\right)}{1-\sqrt{x}+x}\cdot\dfrac{-\sqrt{x}\left(1-\sqrt{x}\right)^2}{2\left(\sqrt{x}-\dfrac{1}{2}\right)}\right]\)
\(=1-\left[\dfrac{-\sqrt{x}\left(1-\sqrt{x}\right)}{2}+\dfrac{-x\left(1-\sqrt{x}\right)^2}{2\left(1-\sqrt{x}+x\right)}\right]\)
rồi làm sao nữa ak?? Tớ có quy đồng lên, tính sơ sơ rồi nhưng thấy kq không gọn.
Câu b là : tìm các số nguyên x để M cũng là số nguyên . Nên tớ nghĩ kq sẽ gọn.
NHỜ MẤY CAO NHÂN RA TAY GIÚP VỚI NHAK ^^!
1.Aleft(dfrac{x+2}{xsqrt{x}-1}+dfrac{sqrt{x}}{x+sqrt{x}+1}+dfrac{1}{1-sqrt{x}}right):dfrac{sqrt{x}}{2}2.Bleft(dfrac{2sqrt{x+x+1}}{sqrt{x}+1}right)left(1-dfrac{x-sqrt{x}}{sqrt{x}-1}right):left(1-sqrt{x}right)3.Cleft(dfrac{sqrt{x}+1}{sqrt{x}-1}-dfrac{sqrt{x}-1}{sqrt{x}+1}dfrac{8sqrt{x}}{x-1}right):left(dfrac{sqrt{x}-x-3}{x-1}-dfrac{1}{sqrt{x}-1}right)Làm chi tiết hộ mình với ak mình đang cần gấp!!!
Đọc tiếp
1.A=\(\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2}\)
2.B=\(\left(\dfrac{2\sqrt{x+x+1}}{\sqrt{x}+1}\right)\left(1-\dfrac{x-\sqrt{x}}{\sqrt{x}-1}\right):\left(1-\sqrt{x}\right)\)
3.C=\(\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\dfrac{8\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}-x-3}{x-1}-\dfrac{1}{\sqrt{x}-1}\right)\)
Làm chi tiết hộ mình với ak mình đang cần gấp!!!
1: Ta có: \(A=\left(\dfrac{x+2}{x\sqrt{x}-1}+\dfrac{\sqrt{x}}{x+\sqrt{x}+1}+\dfrac{1}{1-\sqrt{x}}\right):\dfrac{\sqrt{x}}{2}\)
\(=\dfrac{x+2+x-\sqrt{x}-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{2}{\sqrt{x}}\)
\(=\dfrac{2\sqrt{x}-2}{\sqrt{x}\left(x+\sqrt{x}+1\right)}\)
Đúng 0
Bình luận (0)
Rút gọn:
1) \(P=\left(\dfrac{\sqrt{x}}{2}-\dfrac{1}{2\sqrt{x}}\right):\left(\dfrac{x-\sqrt{x}}{\sqrt{x}+1}-\dfrac{x-\sqrt{x}}{\sqrt{x}+1}-\dfrac{x+\sqrt{x}}{\sqrt{x}-1}\right)\)
2) \(P=\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{\sqrt{x}-1}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
Giúp mk nhé :3
a) \(\left(\dfrac{1}{\sqrt{x}}-\dfrac{1}{x}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}-\dfrac{\sqrt{x}+2}{\sqrt{x}-1}\right)\)
b) \(\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right).\left(\sqrt{a}-\dfrac{1}{a}\right)\)
Cho x>1 .Hãy rút gọn đa thức sau:
\(M=1-\left[\left(\dfrac{1}{\sqrt{x}-1}-\sqrt{x-1}\right):\left(\dfrac{1}{\sqrt{x+1}}-\dfrac{1}{\sqrt{x-1}}\right):\dfrac{\sqrt{x}+1.\sqrt{x^2-1}}{\left(x-1\right)\sqrt{x+1}-\left(x+1\right).\sqrt{x-1}}\right]\)
\(\left(\dfrac{1}{\sqrt{1+x}}+\sqrt{1-x}\right):\left(\dfrac{1}{\sqrt{1-x^2}}+1\right)\)
1. \(\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}-1}{\sqrt{x}}+\dfrac{1-\sqrt{x}}{x+\sqrt{x}}\right)\)
1:
\(=\dfrac{x-1}{\sqrt{x}}:\dfrac{x-1+1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}}\)
2: \(=\dfrac{1+\sqrt{1-x^2}}{\sqrt{1+x}}:\dfrac{1+\sqrt{1-x^2}}{\sqrt{1-x^2}}=\sqrt{\dfrac{1-x^2}{1+x}}=\sqrt{1-x}\)
Đúng 0
Bình luận (0)
RÚT GỌN BIỂU THỨC:
20) \(E = \left(\dfrac{x\sqrt{x} - 1}{x - \sqrt{x}} - \dfrac{x\sqrt{x} +1}{x + \sqrt{x}}\right) + \left(\sqrt{x} - \dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x} + 1}{\sqrt{x} - 1} + \dfrac{\sqrt{x} - 1}{\sqrt{x} + 1}\right)\)
\(E=\left(\dfrac{x\sqrt{x}}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right)+\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\) (ĐK: \(x\ne1;x>0\))
\(E=\left[\dfrac{\left(\sqrt{x}\right)^3-1^3}{x-\sqrt{x}}-\dfrac{\left(\sqrt{x}\right)^3+1^3}{x+\sqrt{x}}\right]+\left[\dfrac{x}{\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right]\left[\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(E=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]+\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(E=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right)+\dfrac{\left(\sqrt{x}\right)^2-1^2}{\sqrt{x}}\cdot\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(E=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}}\cdot\dfrac{2x+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(E=\dfrac{2\sqrt{x}}{\sqrt{x}}+\dfrac{2x+2}{\sqrt{x}}\)
\(E=\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}\)
Đúng 4
Bình luận (1)
RÚT GỌN CÁC BIỂU THỨC SAU:21) A left(dfrac{xsqrt{x} + 1}{x - 1} - dfrac{x - 1}{sqrt{x} - 1}right) : left(sqrt{x} + dfrac{sqrt{x}}{sqrt{x} - 1}right) 22) A left(dfrac{x}{sqrt{x} - 1} - sqrt{x}right) : left(dfrac{sqrt{x} + 1}{sqrt{x}} - dfrac{1}{1 - sqrt{x}} + dfrac{2 - x}{x - sqrt{x}}right)23) A left(dfrac{sqrt{x} - 4}{x - 2sqrt{x}} - dfrac{3}{2 - sqrt{x}}right) : left(dfrac{sqrt{x} + 2}{sqrt{x}} - dfrac{sqrt{x}}{sqrt{x} - 2}right)24) A left(dfrac{2x + 1}{xsqrt{x} - 1} + dfrac{1}{1 - sqrt{x}}...
Đọc tiếp
RÚT GỌN CÁC BIỂU THỨC SAU:
21) \(A = \left(\dfrac{x\sqrt{x} + 1}{x - 1} - \dfrac{x - 1}{\sqrt{x} - 1}\right) : \left(\sqrt{x} + \dfrac{\sqrt{x}}{\sqrt{x} - 1}\right) \)
22) \(A = \left(\dfrac{x}{\sqrt{x} - 1} - \sqrt{x}\right) : \left(\dfrac{\sqrt{x} + 1}{\sqrt{x}} - \dfrac{1}{1 - \sqrt{x}} + \dfrac{2 - x}{x - \sqrt{x}}\right)\)
23) \(A = \left(\dfrac{\sqrt{x} - 4}{x - 2\sqrt{x}} - \dfrac{3}{2 - \sqrt{x}}\right) : \left(\dfrac{\sqrt{x} + 2}{\sqrt{x}} - \dfrac{\sqrt{x}}{\sqrt{x} - 2}\right)\)
24) \(A = \left(\dfrac{2x + 1}{x\sqrt{x} - 1} + \dfrac{1}{1 - \sqrt{x}}\right) : \left(1 - \dfrac{x - 2}{x + \sqrt{x} + 1}\right)\)
25) \(A = 1 : \left(\dfrac{x + 2\sqrt{x} - 2}{x\sqrt{x} + 1} - \dfrac{\sqrt{x} -1}{x - \sqrt{x} + 1} + \dfrac{1}{\sqrt{x} + 1}\right)\)
26) \(A = \left(\dfrac{\sqrt{x}}{\sqrt{x} + 2} - \dfrac{3}{2 - \sqrt{x}} + \dfrac{3\sqrt{x} - 2}{x - 2}\right) : \left(\dfrac{\sqrt{x} + 3}{\sqrt{x} - 2} + \dfrac{2\sqrt{x}}{2\sqrt{x} - x}\right)\)
27) \(P = \left(\dfrac{4\sqrt{x}}{2 + \sqrt{x}} + \dfrac{8}{4 - x}\right) : \left(\dfrac{\sqrt{x} - 1}{x - 2\sqrt{x}} - \dfrac{2}{\sqrt{x}}\right)\)
21: ĐKXĐ: x>0; x<>1
\(A=\left(\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right):\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+\sqrt{x}}{\sqrt{x}-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}-x+\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}-1}{x}\)
\(=\dfrac{-x+\sqrt{x}+2}{\sqrt{x}+1}\cdot\dfrac{1}{x}\)
\(=\dfrac{-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}=\dfrac{-\sqrt{x}+2}{x}\)
22:
DKXĐ: x>0; x<>1
\(A=\dfrac{x-\sqrt{x}\left(\sqrt{x}-1\right)}{\sqrt{x}-1}:\left(\dfrac{\sqrt{x}+1}{\sqrt{x}}+\dfrac{1}{\sqrt{x}-1}+\dfrac{2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\right)\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)+\sqrt{x}+2-x}{\sqrt{x}\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{x-1+\sqrt{x}+2-x}\)
\(=\dfrac{x}{\sqrt{x}+1}\)
23: ĐKXĐ: x>0; x<>4
\(A=\dfrac{\sqrt{x}-4+3\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-2\right)}:\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)-x}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}-4}{\sqrt{x}\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{-4}\)
\(=\dfrac{-4\sqrt{x}+4}{4}=-\sqrt{x}+1\)
24: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{2x+1-x-\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}:\dfrac{x+\sqrt{x}+1-x+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+3}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
25:
ĐKXĐ: x>=0; x<>1
\(A=1:\dfrac{x+2\sqrt{x}-2-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)+x-\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{2x+\sqrt{x}-1-x+1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{x+\sqrt{x}}=\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\)
27: ĐKXĐ: x>0; x<>4
\(P=\dfrac{4\sqrt{x}\left(\sqrt{x}-2\right)-8}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}:\dfrac{\sqrt{x}-1-2\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4x-8\sqrt{x}-8}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}-2\right)}{x-1-2\sqrt{x}+1}\)
\(=\dfrac{4\left(x-2\sqrt{x}-2\right)}{\sqrt{x}+2}\cdot\dfrac{\sqrt{x}}{-\sqrt{x}}\)
\(=\dfrac{-4\left(x-2\sqrt{x}-2\right)}{\sqrt{x}+2}\)
Đúng 1
Bình luận (3)
Rút gọn
A=\(\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right)\div\left(\dfrac{\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\)
B=\(\left(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right)\div\dfrac{\sqrt{x}-1}{x+2\sqrt{x}+1}+1\)
\(A=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}+1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\left(x>0,x\ne9\right)\)
\(=\left(\dfrac{\sqrt{x}}{\sqrt{x}+3}+\dfrac{2x}{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-3\right)}-\dfrac{2}{\sqrt{x}}\right)\)
\(=\dfrac{\sqrt{x}\left(3-\sqrt{x}\right)+2x}{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)}:\dfrac{\sqrt{x}+1-2\left(\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x+3\sqrt{x}}{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)}:\dfrac{7-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-3\right)}\)
\(=\dfrac{\sqrt{x}\left(\sqrt{x}+3\right)}{\left(3-\sqrt{x}\right)\left(\sqrt{x}+3\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{7-\sqrt{x}}=\dfrac{x}{\sqrt{x}-7}\)
\(B=\left(\dfrac{1}{x+\sqrt{x}}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}-1}{x+2\sqrt{x}+1}+1\left(x>0,x\ne1\right)\)
\(=\left(\dfrac{1}{\sqrt{x}\left(\sqrt{x}+1\right)}-\dfrac{1}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+1\right)^2}+1\)
\(=\dfrac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\left(\sqrt{x}+1\right)^2}{\sqrt{x}-1}+1=-\dfrac{\sqrt{x}+1}{\sqrt{x}}+1\)
\(=\dfrac{\sqrt{x}-\sqrt{x}-1}{\sqrt{x}}=-\dfrac{1}{\sqrt{x}}\)
Đúng 1
Bình luận (0)