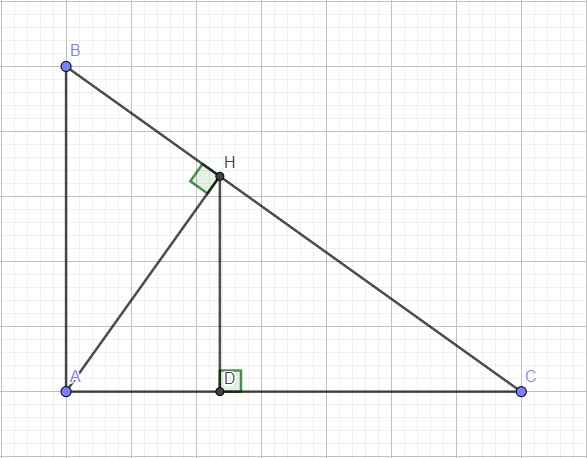
Cho tam giác ABC vuông tại A, đường cao AH, AH =2cm, góc ACB = 30 độ. Tính AC và AB

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, đường cao AH, góc ACB = 30 độ, phân giác góc ABC cắt AH tại E. Tính các tỉ số BH/AH và sBHE/sCAB (s là diện tích tam giác)
Dễ thấy \(\widehat{BAH}=90^o-\widehat{B}=\widehat{C}\), mà \(\widehat{C}=30^o\) nên \(\widehat{BAH}=30^o\). Trong tam giác ABH vuông tại H, ta có \(\dfrac{BH}{AH}=\tan\widehat{BAH}=\tan30^o=\dfrac{\sqrt{3}}{3}\).
Trước hết ta tính \(\dfrac{S_{BHE}}{S_{ABH}}\). Để ý rằng \(\dfrac{S_{BHE}}{S_{ABH}}=\dfrac{EH}{AH}\). Mặt khác, \(\dfrac{EH}{AE}=\dfrac{BH}{AB}=\sin\widehat{BAH}=\sin30^o=\dfrac{1}{2}\) \(\Rightarrow\dfrac{EH}{AH}=\dfrac{1}{3}\) hay \(\dfrac{S_{BHE}}{S_{ABH}}=\dfrac{1}{3}\) (*). Lại thấy \(\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{BH}{BC}\), mà \(\dfrac{BH}{AB}=\dfrac{1}{2}\Rightarrow BH=\dfrac{1}{2}AB\) và \(\dfrac{AB}{BC}=\sin\widehat{C}=\sin30^o=\dfrac{1}{2}\) \(\Rightarrow AB=\dfrac{1}{2}BC\). Từ đó suy ra \(BH=\dfrac{1}{4}BC\) hay \(\dfrac{BH}{BC}=\dfrac{1}{4}\) hay \(\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{1}{4}\) (**)
Từ (*) và (**) \(\Rightarrow\dfrac{S_{BHE}}{S_{ABH}}.\dfrac{S_{ABH}}{S_{ABC}}=\dfrac{1}{3}.\dfrac{1}{4}\Rightarrow\dfrac{S_{BHE}}{S_{ABC}}=\dfrac{1}{12}\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A có BC = 10cm , góc C = 30 độ .
a. Tính AB , AC
b. Tính đường cao AH
a) Xét ΔABC vuông tại A có
\(AB=BC\cdot\sin30^0\)
\(=10\cdot\dfrac{1}{2}=5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=10^2-5^2=75\)
hay \(AC=5\sqrt{3}\left(cm\right)\)
b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=5\cdot5\sqrt{3}=25\sqrt{3}\)
hay \(AH=\dfrac{25\sqrt{3}}{10}=\dfrac{5\sqrt{3}}{2}\left(cm\right)\)
Đúng 4
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 3cm, AC = 4cm. Tính độ dài các cạnh BC, AH và số đo góc ACB (làm tròn đến độ).
Tham khảo tại đây nha:
https://hoc24.vn/hoi-dap/question/887221.html
Đúng 3
Bình luận (1)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=3^2+4^2=25\)
hay BC=5cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot5=3\cdot14=12\)
hay AH=2,4cm
Đúng 2
Bình luận (0)
2.cho tam giác ABC có AB= 12cm, góc ABC = 40 độ , góc ACB =30 độ , đường cao AH .Tính AH, AC
Lời giải:
Xét tam giác vuông $ABH$:
$\frac{AH}{AB}=\sin B\Rightarrow AH=AB.\sin B=12.\sin 40^0=12\sin 40^0=7,71$ (cm)
Xét tam giác vuông $AHC$:
$\frac{AH}{AC}=\sin C\Rightarrow AC=\frac{AH}{\sin C}=\frac{7,71}{\sin 30^0}=15,42$ (cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. a) Biết AB = 2cm, AC =2/3 m. Tính độ dài BC, AH và số đo góc B. b) Gọi E là trung điểm AC của tam giác ABC và K là hình chiếu vuông góc của A lên BE. Chứng minh BK BE = BH BC và tam giác KEC đồng dạng với tam giác CEB c) Giả thiết rằng tia CK đồng thời là phân giác của góc C của tam giác ABC. Chứng minh 2.cos B = taB
Cho ΔABC vuông tại A, đường cao AH và đường phân giác AD (H và D thuộc BC). Biết AB = 21cm, AC = 28cm.
a) Tính diện tích tam giác ABC và chứng minh AH . BC = AB . AC
b) Tính độ dài BC, DB và DC.
c) Đường phân giác BK của góc ABC cắt AD tại I (K thuộc AC), tính tỉ số BI/IK. Gọi G là trọng tâm ΔABC, chứng minh IG //AC.
Cho tam giác ABC vuông tại A, vẽ đường cao AH của tam giác ABC (H thuộc BC).1) Nếu sin ACB 3/5 và BC 20 cm. Tính các cạnh AB, AC, BH và góc ACB (số đo góc làm tròn đến độ)2) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. Chứng minh: AD.AC BH.BC.3) Kẻ tia phân giác BE của DBA ( E thuộc đoạn DA). Chứng minh: tan EBA AD/AB + BD4) Lấy điểm K thuộc đoạn AC, Kẻ KM vuông góc với HC tại M, KN vuông góc với AH tại N. chứng minh : NH.NA+MH.MCKA.KC
Đọc tiếp
Cho tam giác ABC vuông tại A, vẽ đường cao AH của tam giác ABC (H thuộc BC).
1) Nếu sin ACB = 3/5 và BC = 20 cm. Tính các cạnh AB, AC, BH và góc ACB (số đo góc làm tròn đến độ)
2) Đường thẳng vuông góc với BC tại B cắt đường thẳng AC tại D. Chứng minh: AD.AC = BH.BC.
3) Kẻ tia phân giác BE của DBA ( E thuộc đoạn DA). Chứng minh: tan EBA = AD/AB + BD
4) Lấy điểm K thuộc đoạn AC, Kẻ KM vuông góc với HC tại M, KN vuông góc với AH tại N. chứng minh : NH.NA+MH.MC=KA.KC
2: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=AB^2\left(1\right)\)
Xét ΔBDC vuông tại B có BA là đường cao ứng với cạnh huyền DC
nên \(AD\cdot AC=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BC=AD\cdot AC\)
Đúng 4
Bình luận (0)
Cho tam giác ABC nhọn có đường cao AH. Kẻ HD vuông góc với AB tại D. Cho AH=8 cm, AB=10 cm
a,Tính HB, HD
b,Kẻ HE vuông góc với AC tại E. CMR: AD.AB=AE.AC
c, Biết góc ACB=30 độ, tính diện tích tứ giác BDEC
Cho tam giác ABC vuông tại A, đường cao AH=6cm, HC =8cm
a) tính độ dài HB,BC,AB,AC
b) Kẻ HD vuông góc với AC ( D thuộc AC). Tính độ dài HD và diện tích tam giác AHD
giúp mình với ạ
Áp dụng định lý Pitago cho tam giác vuông ACH:
\(AC=\sqrt{AH^2+HC^2}=10\left(cm\right)\)
Áp dụng hệ thức lượng cho tam giác vuông ABC:
\(AC^2=CH.BC\Rightarrow BC=\dfrac{AC^2}{CH}=\dfrac{25}{2}\) (cm)
\(\Rightarrow BH=BC-CH=\dfrac{9}{2}\left(cm\right)\)
Pitago tam giác vuông ABC:
\(AB=\sqrt{BC^2-AC^2}=\dfrac{15}{2}\left(cm\right)\)
b.
Áp dụng hệ thức lượng cho tam giác vuông ACH:
\(HD.AC=AH.HC\Rightarrow HD=\dfrac{AH.HC}{AC}=\dfrac{24}{5}\left(cm\right)\)
Tiếp tục là hệ thức lượng:
\(AH^2=AD.AC\Rightarrow AD=\dfrac{AH^2}{AC}=\dfrac{18}{5}\left(cm\right)\)
\(S_{AHD}=\dfrac{1}{2}AD.HD=\dfrac{216}{25}\left(cm^2\right)\)
Đúng 3
Bình luận (0)