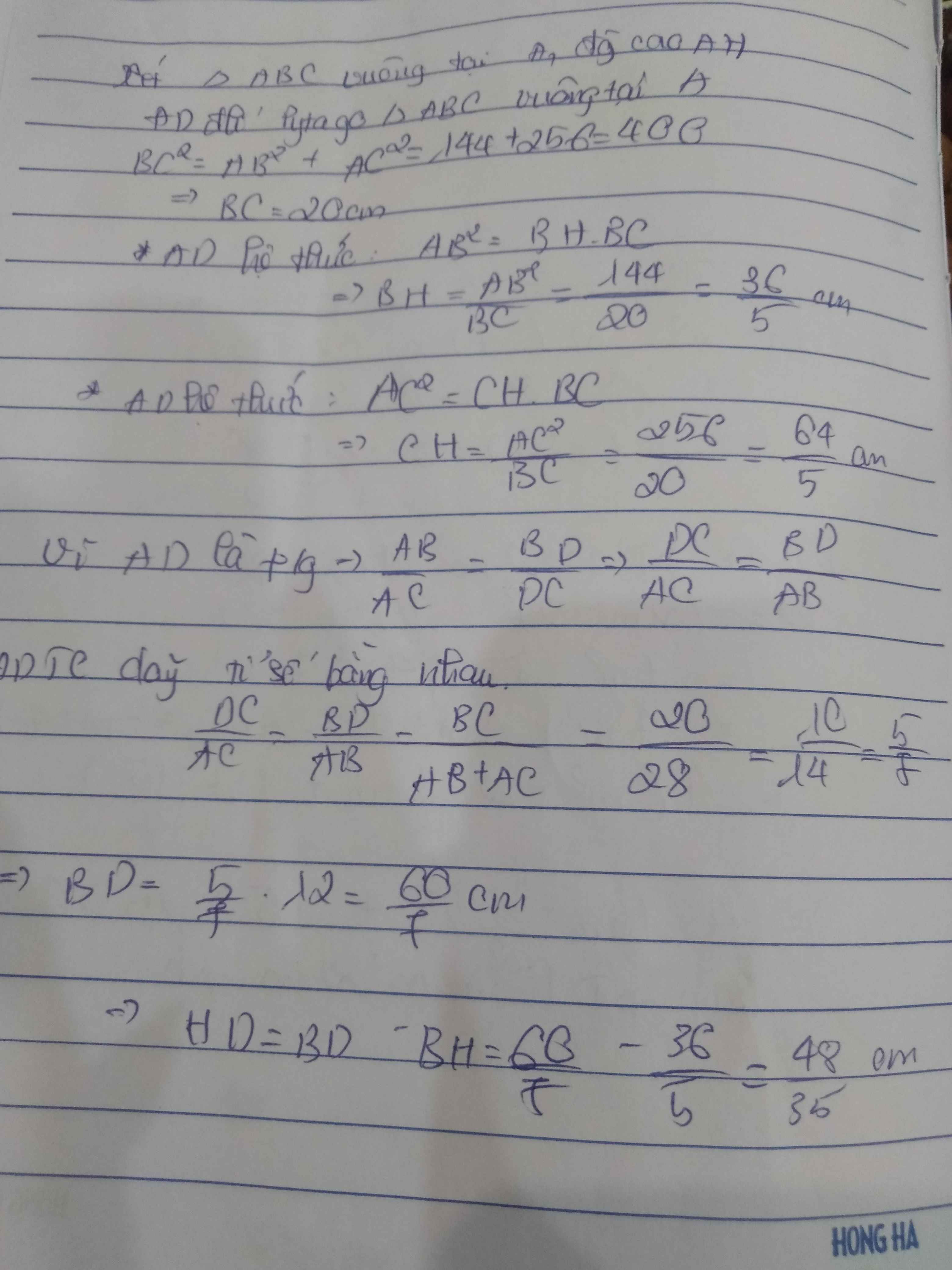cho tam giác ABC vuông ở A AH là đường cao biết AH=12cm HC=16cm tinh chu vu tam giac ABC. cmr AM AB =AN AC .AHmu3=BM.CN.BC

Những câu hỏi liên quan
1. Cho tam giác ABC vuông tại A(AB<AC) có đường cao AH. Biết BC = 25cm, AH = 12cm. Tính AB, AC, BH, CH
2. Cho tam giác ABC vuồng tại A, đường cao AH. Biết AB = 15cm, HC = 16cm. Tính AC, BC, AH, BH
cho tam giác ABC vuông tại A , AB = 12cm , AC = 16cm , tia phân giác AD , đường cao Ah , Tinh HD , HB , HC
tự vẽ hình..
\(BC=\sqrt{AC^2+AB^2}=\sqrt{12^2+16^2}=20cm\)( Định lý pitago cho tam giác vuông ABC)
\(\Rightarrow BH=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2cm\)( Áp dụng hệ thức lương cho tam giác vuông ABC)
\(HC=BC-HB=20-7,2=12,8cm\)
Đúng 0
Bình luận (0)
Áp dụng tính chất tia phân giác: \(\frac{BD}{AB}=\frac{CD}{AC}=\frac{BD+CD}{AB+AC}=\frac{BC}{12+16}=\frac{20}{12+16}=\frac{5}{7}\)
\(\Rightarrow BD=\frac{AB.5}{7}=\frac{12.5}{7}\approx8,571\)( chả biết ý này có đ ko nx)
Đúng 0
Bình luận (1)
1. Cho ∆ABC biết BC = 7.5cm, AC = 4.5cm, AB = 6cm.
a) ∆ABC là tam giác gì? Tính đường cao AH của ∆ABC.
b) Tính độ dài các cạnh BH, HC.
2. Cho ∆ABC vuông tại A, AB = 12cm, AC = 16cm, phân giác AD, đường cao AH. Tính HD, HB, HC.
1)
a) Xét ΔABC có
\(BC^2=AC^2+AB^2\left(7.5^2=4.5^2+6^2\right)\)
nên ΔABC vuông tại A(Định lí Pytago đảo)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A, ta được:
\(AB\cdot AC=AH\cdot BC\)
\(\Leftrightarrow AH=\dfrac{AB\cdot AC}{BC}=\dfrac{4.5\cdot6}{7.5}=\dfrac{27}{7.5}=3.6\left(cm\right)\)
Vậy: AH=3,6cm
b) Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=AH^2+CH^2\)
\(\Leftrightarrow CH^2=4.5^2-3.6^2=7.29\)
hay CH=2,7(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH=BC-CH=7,5-2,7=4,8(cm)
Vậy: BH=4,8cm; CH=2,7cm
Đúng 3
Bình luận (0)
1.a)Ta có:7,52=4,52+62 nên theo định lí Py-ta-go
=>\(\Delta ABC\) vuông tại A
Ta có: AB.AC=BC.AH
=> \(AH=\dfrac{AC.AB}{BC}=\dfrac{4,5.6}{7,5}=3.6\) (cm)
Đúng 2
Bình luận (0)
b)Ta có:AB2=BC.BH
\(\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{7,5}=4,8\) (cm)
Ta có:BH+CH=BC
=>CH=BC-BH=7,5-4,8=2,7 (cm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A AB=12cm AC=16cm duong phan giac AD đường cao AH tinh BH,CH,DH
Áp dụng hệ thức lượng tìm được \(BH=\frac{36}{5};CH=\frac{64}{5}\)(cm)
Áp dụng tính chất đường phân giác tìm được \(\frac{BD}{DC}=\frac{AB}{AC}\Leftrightarrow\frac{BD}{BC}=\frac{AB}{AB+AC}\Leftrightarrow\frac{BD}{20}=\frac{12}{12+16}=\frac{12}{28}\Rightarrow BD=\frac{20\cdot12}{28}=\frac{60}{7}\)
\(\Rightarrow HD=BD-BH=\frac{60}{7}-\frac{36}{5}=\frac{300-252}{35}=\frac{48}{35}\)(cm)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A . Biết AB = 12cm , AC = 16cm,phân giác AD , đường cao AH . Tính HD , HB , HC.
Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
(HC tự tính nha)
Đúng 5
Bình luận (1)
Cho tam giác ABC vuông tại A, kẻ đường cao AH
a)Biết HB=50cm, HC= 8cm. Tính chu vi tam giác ABC
b)Biết AC=12cm, HC=6cm. Tính AH, AB
c)Biết AH=12cm, BC=25cm. Tính AB+AC
Em xin cảm ơn ạ❤
a) \(AH^2=HB.HC=50.8=400\)
\(\Rightarrow AH=20\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.20\left(50+8\right)=\dfrac{1}{2}.20.58\left(cm^2\right)\)
mà \(S_{ABC}=\dfrac{1}{2}AB.AC\)
\(\Rightarrow AB.AC=20.58=1160\)
Theo Pitago cho tam giác vuông ABC :
\(AB^2+AC^2=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2-2AB.AC=BC^2\)
\(\Rightarrow\left(AB+AC\right)^2=BC^2+2AB.AC\)
\(\Rightarrow\left(AB+AC\right)^2=58^2+2.1160=5684\)
\(\Rightarrow AB+AC=\sqrt[]{5684}=2\sqrt[]{1421}\left(cm\right)\)
Chu vi Δ ABC :
\(AB+AC+BC=2\sqrt[]{1421}+58=2\left(\sqrt[]{1421}+29\right)\left(cm\right)\)
Đúng 1
Bình luận (0)
có ai biết giải bài này k giải hộ mình vs ( mình cảm ơn )bài 1: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB15cm; HC16cm. tính BC,AC,AH.câu 2: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AH12cm; BC25cm. tính AB,ACbài 3: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB6cm; BH3cm. tính AH,AC,CH.bài 4: cho tam giác ABC vuông tại A kẻ đường cao AH. tính diện tích tam giác ABC biết AH12cm; BH9cm.bài 5: cho tam giác vuông , biết sỉ số của các cạnh góc vuông làdfrac{5}{12} cạ...
Đọc tiếp
có ai biết giải bài này k giải hộ mình vs ( mình cảm ơn )
bài 1: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB=15cm; HC=16cm. tính BC,AC,AH.
câu 2: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AH=12cm; BC=25cm. tính AB,AC
bài 3: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB=6cm; BH=3cm. tính AH,AC,CH.
bài 4: cho tam giác ABC vuông tại A kẻ đường cao AH. tính diện tích tam giác ABC biết AH=12cm; BH=9cm.
bài 5: cho tam giác vuông , biết sỉ số của các cạnh góc vuông là\(\dfrac{5}{12}\) cạnh huyền là 26. tính độ dài các cạnh góc vuông và hình chiếu các cạnh góc vuông trên cạnh huyền.
bài 6: cho tam giác ABC vuông tại A. biết \(\dfrac{AB}{AC}\) =\(\dfrac{5}{7}\). đường cao AH=15cm. tính HB,HC
có ai biết giải bài này k giải hộ mình vs ( mình cảm ơn )bài 1: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB15cm; HC16cm. tính BC,AC,AH.câu 2: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AH12cm; BC25cm. tính AB,ACbài 3: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB6cm; BH3cm. tính AH,AC,CH.bài 4: cho tam giác ABC vuông tại A kẻ đường cao AH. tính diện tích tam giác ABC biết AH12cm; BH9cm.bài 5: cho tam giác vuông , biết sỉ số của các cạnh góc vuông là512512 cạnh huy...
Đọc tiếp
có ai biết giải bài này k giải hộ mình vs ( mình cảm ơn )
bài 1: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB=15cm; HC=16cm. tính BC,AC,AH.
câu 2: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AH=12cm; BC=25cm. tính AB,AC
bài 3: cho tam giác ABC vuông tại A kẻ đường cao AH. biết AB=6cm; BH=3cm. tính AH,AC,CH.
bài 4: cho tam giác ABC vuông tại A kẻ đường cao AH. tính diện tích tam giác ABC biết AH=12cm; BH=9cm.
bài 5: cho tam giác vuông , biết sỉ số của các cạnh góc vuông là512512 cạnh huyền là 26. tính độ dài các cạnh góc vuông và hình chiếu các cạnh góc vuông trên cạnh huyền.
bài 6: cho tam giác ABC vuông tại A. biết ABACABAC =5757. đường cao AH=15cm. tính HB,HC
nhờ các bạn giải giúp hộ mình vs ạ mình cần gấp
Đúng 0
Bình luận (0)
Cho tam giác ABC, biết AB=12cm, BC=20cm, AC=16cm
a. Chứng minh tam giác ABC là tam giác vuông
b. Vẽ đường cao AH. Tính AH,BH
c. Giải tam giác vuông ACH
d. Vẽ phân giác AD. Tính DB, DC
e. Tinh cosB trong hai tam giac vuong HBA va ABC . suy ra AB2= BH.BC