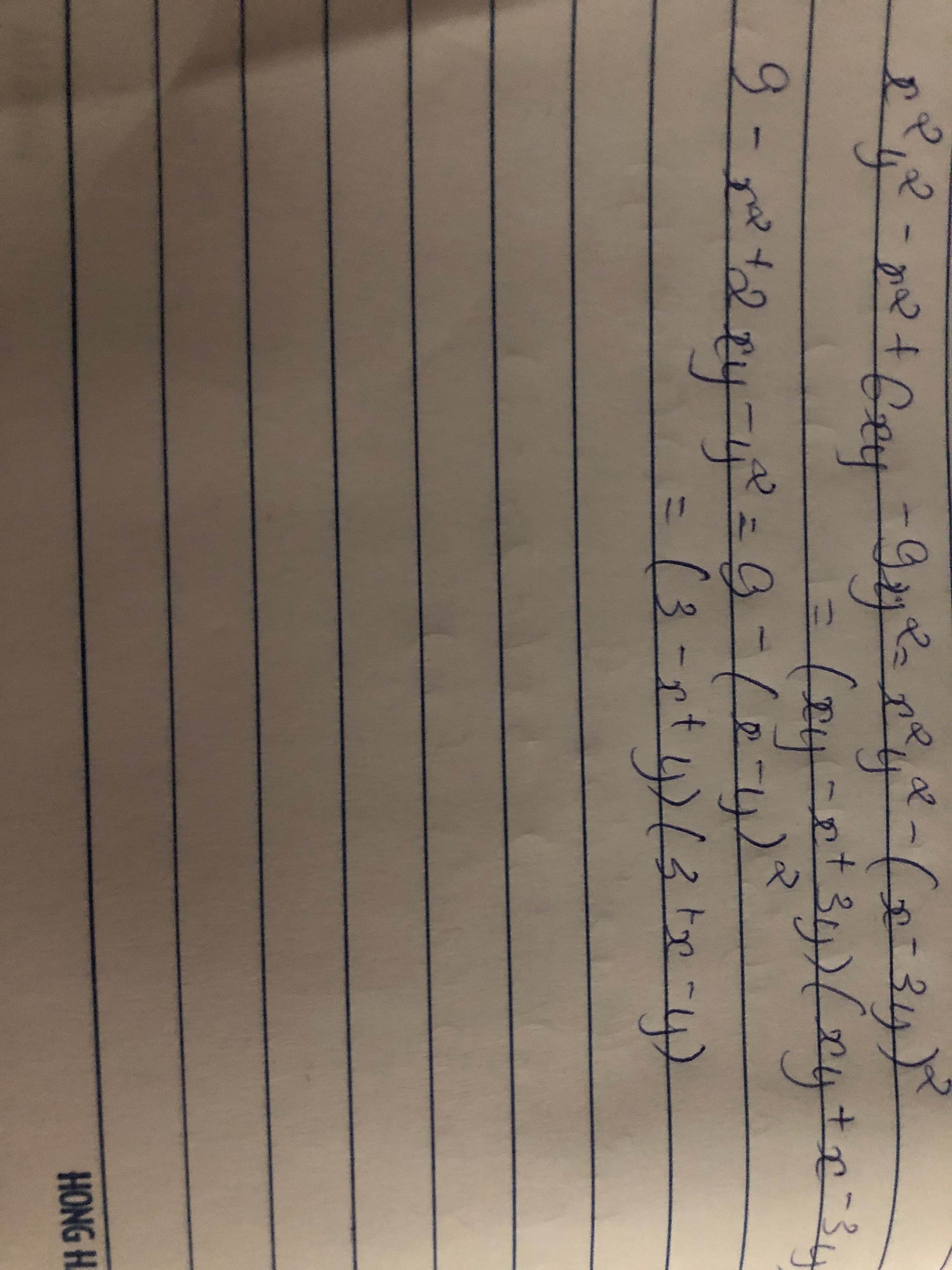help me Phân tích đa thức-> nhan tử
3x^2(x-1)+5x(1-x)^2
3(x-y)^2+9y(y-x)^2
3(x-y)^2+9y(y-x)

Những câu hỏi liên quan
Bài 1: Phân tích đa thức thành nhân tử:
a) 3(x-y)^2+9y(y-x)^2
b) 3(x-y)^2+9y(y-x)
giúp e với ạ, em cảm ơn
a) \(3\left(x-y\right)^2+9y\left(y-x\right)^2\)
\(=3\left(x-y\right)^2+9y\left(x-y\right)^2\)
\(=\left(x-y\right)^2\left(3-9y\right)\)
\(=3\left(x-y\right)^2\left(3y+1\right)\)
b) \(3\left(x-y\right)^2+9y\left(y-x\right)\)
\(=3\left(y-x\right)^2+9y\left(y-x\right)\)
\(=\left(y-x\right)\left[3\left(y-x\right)+9y\right]\)
\(=3\left(y-x\right)\left(y-x+3y\right)\)
\(=3\left(y-x\right)\left(4y-x\right)\)
Đúng 2
Bình luận (1)
a: =3(x-y)^2+9y(x-y)^2
=(x-y)^2(3+9y)
=(x-y)^2*3*(y+3)
b: =3(x-y)^2-9y(x-y)
=3(x-y)(x-y-9y)
=3(x-y)(x-10y)
Đúng 1
Bình luận (4)
phân tích đa thức thành nhan tử
x^4 -10x^2 y^2 + 9y^2
(x^2-8)^2 + 36
x^4 - 53x^2 y^2 +196y^2
phân tích đa thức thành nhan tử
x^4 -10x^2 y^2 + 9y^2
(x^2-8)^2 + 36
x^4 - 53x^2 y^2 +196y^2
phân tích đa thức sau thành nhan tử
1, ( x mũ 2 - 9y mũ 2 ) - ( 4x + 12y )
3, - x mũ 2 + 2xy - y mũ 2 + 25
5, x mũ 3 - 6x mũ 2 + 9
7, x mũ 3 - x mũ 2 y - xy mũ 2 + y mũ 3
9, 9 ( x - 1 ) - 4( 2x + 3 ) mũ 2
\(1,\)
\(\left(x^2-9y^2\right)\left(4x+12y\right)\)
\(=\left(x-3y\right)\left(x+3y\right)-4\left(x+3y\right)\)
\(=\left(x+3y\right)\left(x-3y-4\right)\)
\(3,\)
\(-x^2+2xy-y^2+25\)
\(=-\left(x^2-2xy+y^2\right)+25\)
\(=25-\left(x-y\right)^2\)
\(=5^2-\left(x-y\right)^2\)
\(=\left(5-x+y\right)\left(5+x-y\right)\)
\(5,\)
\(x^3-6x^2+9\)
\(=x\left(x^2-6x+9\right)\)
\(=x\left(x-3\right)^2\)
Xem thêm câu trả lời
Bài 1: Phân tích các đa thức sau thành nhân tử
1)3x(x-1)+5(x-1)
2)4x (x-2y)-8y (2y-x)
3)a^2 (x-1)+b^2 (1-x)
4)3x (x-a) +4a(a-x)
5)5x (x-y)^2 +10y^2(y-x)^2
6)3x(x-3)^2+9(3-x)^2
7)x(m-a)^2-y(a-m)^2
8)6y^2(x-1)^2+9y(1-x)^2
1) \(3x\left(x-1\right)+5\left(x-1\right)\)
\(=\left(x-1\right)\left(3x+5\right)\)
2) \(4x(x-2y)-8y(2y-x)\)
\(=4x\left(x-2y\right)+8y\left(x-2y\right)\)
\(=\left(4x+8y\right)\left(x-2y\right)\)
\(=4\left(x+2y\right)\left(x-2y\right)\)
3) \(a^2\left(x-1\right)+b^2\left(1-x\right)\)
\(=a^2\left(x-1\right)-b^2\left(x-1\right)\)
\(=\left(a^2-b^2\right)\left(x-1\right)\)
\(=\left(a-b\right)\left(a+b\right)\left(x-1\right)\)
4) \(3x\left(x-a\right)+4a\left(a-x\right)\)
\(=3x\left(x-a\right)-4a\left(x-a\right)\)
\(=\left(x-a\right)\left(3x-4a\right)\)
5) \(5x\left(x-y\right)^2+10y^2\left(y-x\right)^2\)
\(=5x\left(x-y\right)^2+10y^2\left(x-y\right)^2\)
\(=\left(5x+10y^2\right)\left(x-y\right)^2\)
\(=5\left(x+2y^2\right)\left(x-y\right)^2\)
6) \(3x\left(x-3\right)^2+9\left(3-x\right)^2\)
\(=3x\left(x-3\right)^2+9\left(x-3\right)^2\)
\(=\left(3x+9\right)\left(x-3\right)^2\)
\(=3\left(x+3\right)\left(x-3\right)^2\)
7) \(x\left(m-a\right)^2-y\left(a-m\right)^2\)
\(=x\left(a-m\right)^2-y\left(a-m\right)^2\)
\(=\left(x-y\right)\left(a-m\right)^2\)
8) \(6y^2\left(x-1\right)^2+9y\left(1-x\right)^2\)
\(=6y^2\left(x-1\right)^2+9y\left(x-1\right)^2\)
\(=\left(6y^2+9x\right)\left(x-1\right)^2\)
\(=3\left(2y^2+3x\right)\left(x-1\right)^2\)
#Ayumu
Đúng 1
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử:1) 3x^3y^2-6xy2) left(x-2yright).left(x+3yright)-2.left(x-2yright)3) left(3x-1right).left(x-2yright)-5x.left(2y-xright)4) x^2-y^2-6y-95) left(3x-yright)^2-4y^26) 4x^2-9y^2-4x+1 8) x^2y-xy^2-2x+2y9) x^2-y^2-2x+2yBài 2: Tìm x:1) left(2x-1right)^2-4.left(2x-1right)02) 9x^3-x03) left(3-2xright)^2-2.left(2x-3right)04) left(2x-5right)left(x+5right)-10x+250
Đọc tiếp
Bài 1: Phân tích đa thức thành nhân tử:
1) \(3x^3y^2-6xy\)
2) \(\left(x-2y\right).\left(x+3y\right)-2.\left(x-2y\right)\)
3) \(\left(3x-1\right).\left(x-2y\right)-5x.\left(2y-x\right)\)
4) \(x^2-y^2-6y-9\)
5) \(\left(3x-y\right)^2-4y^2\)
6) \(4x^2-9y^2-4x+1\)
8) \(x^2y-xy^2-2x+2y\)
9) \(x^2-y^2-2x+2y\)
Bài 2: Tìm x:
1) \(\left(2x-1\right)^2-4.\left(2x-1\right)=0\)
2) \(9x^3-x=0\)
3) \(\left(3-2x\right)^2-2.\left(2x-3\right)=0\)
4) \(\left(2x-5\right)\left(x+5\right)-10x+25=0\)
Bài 2:
1: \(\left(2x-1\right)^2-4\left(2x-1\right)=0\)
=>\(\left(2x-1\right)\left(2x-1-4\right)=0\)
=>(2x-1)(2x-5)=0
=>\(\left[{}\begin{matrix}2x-1=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\)
2: \(9x^3-x=0\)
=>\(x\left(9x^2-1\right)=0\)
=>x(3x-1)(3x+1)=0
=>\(\left[{}\begin{matrix}x=0\\3x-1=0\\3x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
3: \(\left(3-2x\right)^2-2\left(2x-3\right)=0\)
=>\(\left(2x-3\right)^2-2\left(2x-3\right)=0\)
=>(2x-3)(2x-3-2)=0
=>(2x-3)(2x-5)=0
=>\(\left[{}\begin{matrix}2x-3=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\)
4: \(\left(2x-5\right)\left(x+5\right)-10x+25=0\)
=>\(2x^2+10x-5x-25-10x+25=0\)
=>\(2x^2-5x=0\)
=>\(x\left(2x-5\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\2x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{5}{2}\end{matrix}\right.\)
Bài 1:
1: \(3x^3y^2-6xy\)
\(=3xy\cdot x^2y-3xy\cdot2\)
\(=3xy\left(x^2y-2\right)\)
2: \(\left(x-2y\right)\left(x+3y\right)-2\left(x-2y\right)\)
\(=\left(x-2y\right)\cdot\left(x+3y\right)-2\cdot\left(x-2y\right)\)
\(=\left(x-2y\right)\left(x+3y-2\right)\)
3: \(\left(3x-1\right)\left(x-2y\right)-5x\left(2y-x\right)\)
\(=\left(3x-1\right)\left(x-2y\right)+5x\left(x-2y\right)\)
\(=(x-2y)(3x-1+5x)\)
\(=\left(x-2y\right)\left(8x-1\right)\)
4: \(x^2-y^2-6y-9\)
\(=x^2-\left(y^2+6y+9\right)\)
\(=x^2-\left(y+3\right)^2\)
\(=\left(x-y-3\right)\left(x+y+3\right)\)
5: \(\left(3x-y\right)^2-4y^2\)
\(=\left(3x-y\right)^2-\left(2y\right)^2\)
\(=\left(3x-y-2y\right)\left(3x-y+2y\right)\)
\(=\left(3x-3y\right)\left(3x+y\right)\)
\(=3\left(x-y\right)\left(3x+y\right)\)
6: \(4x^2-9y^2-4x+1\)
\(=\left(4x^2-4x+1\right)-9y^2\)
\(=\left(2x-1\right)^2-\left(3y\right)^2\)
\(=\left(2x-1-3y\right)\left(2x-1+3y\right)\)
8: \(x^2y-xy^2-2x+2y\)
\(=xy\left(x-y\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(xy-2\right)\)
9: \(x^2-y^2-2x+2y\)
\(=\left(x^2-y^2\right)-\left(2x-2y\right)\)
\(=\left(x-y\right)\left(x+y\right)-2\left(x-y\right)\)
\(=\left(x-y\right)\left(x+y-2\right)\)
Đúng 0
Bình luận (0)
Phân tích đa thức sau thành nhân tử
a) (5x-4)^2 -49x^2
b) x^3 +2x^2 +xy^2
c) x^2 -y^2 -x+y
d) 4x^2 -9y^2 +4x -6y
e) -x^2 +5x +2xy -5y -y^2
f) y^2 (x^2 +y) -zx^2 -zy
a) \(\left(5x-4\right)^2-49x^2\)
\(=\left(5x-4\right)^2-\left(7x\right)^2\)
\(=\left(12x-4\right)\left(-2x-4\right)\)
\(=-6\left(3x-1\right)\left(x+2\right)\)
c) \(x^2-y^2-x+y\)
\(=\left(x+y\right)\left(x-y\right)-\left(x-y\right)\)
\(=\left(x+y-1\right)\left(x-y\right)\)
d)\(4x^2-9y^2+4x-6y\)
\(=\left(2x-3y\right)\left(2x+3y\right)+2\left(2y-3y\right)\)
\(=\left(2x-3y\right)\left(2x+3y+2\right)\)
Đúng 0
Bình luận (0)
e) \(-x^2+5x+2xy-5y-y^2\)
\(=-\left(x^2-2xy+y^2\right)+\left(5x-5y\right)\)
\(=-\left(x-y\right)^2+5\left(x-y\right)\)
\(=\left(x-y\right)\left(y-x+5\right)\)
f) \(y^2\left(x^2+y\right)-zx^2-zy\)
\(=y^2\left(x^2+y\right)-z\left(x^2+y\right)\)
\(=\left(y^2-z\right)\left(x^2+y\right)\)
Đúng 0
Bình luận (0)
phân tích đa thức thành nhân tử
2)3x^2-6xy+3y^2
3)3(x-y)-5y(y-x)
5)(x+y)^3-(x-y)^3
6)3x^2-5x+2
giúp mình với ạ
2)3x2-6xy+3y2=3(x2-2xy+y2)=3(x-y)2
3)3(x-y)-5y(y-x)=3(x-y)+5y(x-y)=(x-y)(3+5y)
5)(x+y)3-(x-y)3=[(x+y)-(x-y)][(x+y)2+(x+y)(x-y)+(x-y)2]=(x+y-x+y)(x2+2xy+y2+x2-y2+x2-2xy+y2)=2y(3x2+y2)
6)3x2-5x+2=3x2-2x-3x+2=(3x2-3x)-(2x-2)=3x(x-1)-2(x-1)=(x-1)(3x-2)
Đúng 0
Bình luận (0)
Phân tích đa thức thành nhân tử
x^2y^2-x^2+6xy-9y^2
9-x^2+2xy-y^2
a) Ta có: \(x^2y^2-x^2+6xy-9y^2\)
\(=x^2y^2-\left(x^2-6xy+y^2\right)\)
\(=\left(xy\right)^2-\left(x-3y\right)^2\)
\(=\left(xy-x+3y\right)\left(xy+x-3y\right)\)
b) Ta có: \(9-x^2+2xy-y^2\)
\(=9-\left(x^2-2xy+y^2\right)\)
\(=9-\left(x-y\right)^2\)
\(=\left(9-x+y\right)\left(9+x-y\right)\)
Đúng 0
Bình luận (0)