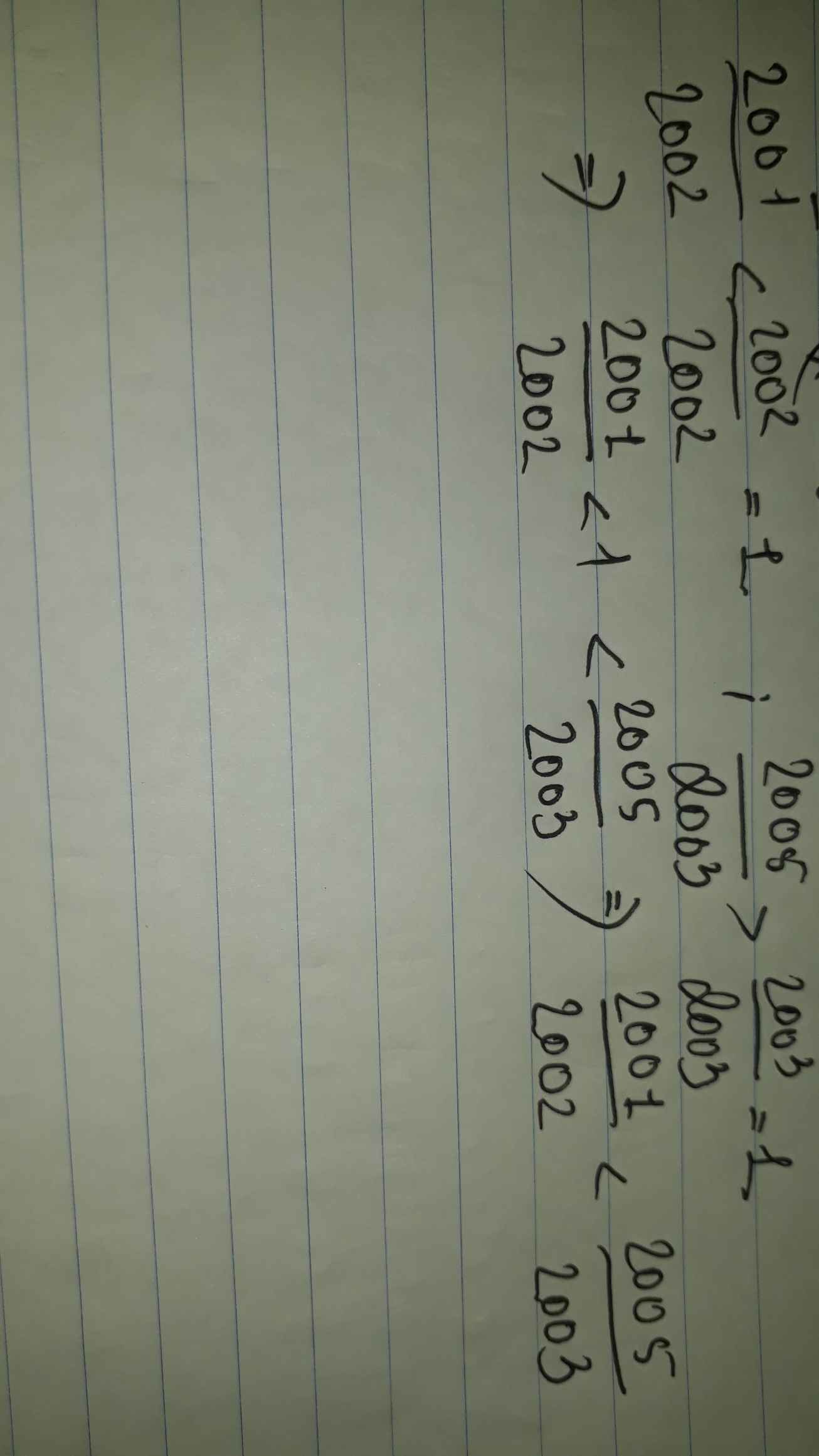ta có\(\dfrac{2001}{2002}< 1\)và\(\dfrac{2005}{2003}>1\)

\(\Rightarrow\dfrac{2001}{2002}< \dfrac{2005}{2003}\)

Ta có: \(\dfrac{2001}{2002}< 1\)

mà \(1< \dfrac{2005}{2003}\)

nên \(\dfrac{2001}{2002}< \dfrac{2005}{2003}\)

1) Áp dụng BĐT \(\frac{a}{b}>\frac{a-m}{b-m}\) với \(\frac{a}{b}< 1\) .Dễ dàng chứng minh Bđt trên, áp dụng vào ta có: 

a) \(x=\frac{2002}{2003}=\frac{2002-1+1}{2003-1+1}=\frac{2003-1}{2004-1}< \frac{2003}{2004}\)

Với \(\frac{a}{b}=\frac{2003}{2004};\frac{a-m}{b-m}=\frac{2003-1}{2004-1}\)

Từ đó ta có: x < y

b) Vì đây là phân số âm nên bé hơn phân số dương nên ta có BĐT: \(\frac{a}{b}>\frac{c}{d}\Leftrightarrow\frac{-a}{b}< \frac{-c}{d}\) 

Áp dụng vào bài toán trên với \(\frac{a}{b}=\frac{2002}{2003}< 1\)và \(\frac{c}{d}=\frac{2005}{2004}>1\)

Nên \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow\frac{-a}{b}>\frac{-c}{d}\)hay x > y

Bài 1 :

a, Ta có : \(x=\frac{2002}{2003}=1-\frac{1}{2003}\)

               \(y=\frac{2003}{2004}=1-\frac{1}{2004}\)

Vì \(\frac{1}{2003}>\frac{1}{2004}\)

\(\Rightarrow1-\frac{1}{2003}< 1-\frac{1}{2004}\)

\(\Rightarrow x< y\)

b, Ta thấy cả 2 vế đều có dấu âm nên ta rút gọn dấu âm đi thì được : 

\(x=\frac{2002}{2003}\)                                                                             \(y=\frac{2005}{2004}\)

Lúc này : 

Ta có : \(y=\frac{2005}{2004}>1=\frac{2003}{2003}>\frac{2002}{2003}=x\)

Vì khi so sánh dương sẽ đối ngược với so sánh âm :

\(\Rightarrow\)Khi trả lại dấu âm thì tất nhiên \(x=\frac{-2002}{2003}>y=\frac{2005}{-2004}\)

Vậy \(x>y\)

Bài 2 :

 Ta quy đồng các phân số trên như sau : 

\(\frac{-2}{7}=\frac{-6}{21}\)                                                                                                      \(\frac{-2}{9}=\frac{-6}{27}\)

Gọi các phân số thỏa mãn điều kiện trên là x .

Ta có : \(\frac{-6}{21}< x< \frac{-6}{27}\)

\(\Rightarrow x\in\left\{\frac{-6}{22};\frac{-6}{23};\frac{-6}{24};\frac{-6}{25};\frac{-6}{26}\right\}\)

Ta rút gọn và dấu của các phân số như sau ( nếu không rút gọn được thì cúng đừng chuyển dấu ) : 

\(x\in\left\{\frac{3}{-11};\frac{-6}{23};\frac{3}{-12};\frac{-6}{25};\frac{3}{-13}\right\}\)

Vậy các phân số thỏa mãn đề bài là : \(\frac{3}{-11};\frac{3}{-12};\frac{3}{-13}\).

minh cảm ơn

mỗi  số hạng trong biểu thức A đều nhỏ hơn 1 mà có 15 số nên tổng A sẽ nhỏ hơn 15

ta thay tong tren <1+1+1+1+1+1+1+1+1+1+1+1+1+1+1

hay tong tren be hon 15

a.\(\frac{13}{17}\)=1-\(\frac{4}{17}\);    \(\frac{46}{50}\)=1-\(\frac{4}{50}\)

Vì \(\frac{4}{17}\)>\(\frac{4}{50}\)=> 1-\(\frac{4}{17}\)<1-\(\frac{4}{50}\)

Vậy\(\frac{13}{17}\)<\(\frac{46}{50}\)

c.\(\frac{41}{91}\)=1-\(\frac{50}{91}\)=1-\(\frac{500}{910}\);    \(\frac{411}{911}\)=1-\(\frac{500}{911}\)

Vì \(\frac{500}{910}\)>\(\frac{500}{911}\)=>1-\(\frac{500}{910}\)<1-\(\frac{500}{911}\)=>\(\frac{41}{91}\)<\(\frac{411}{911}\)

d. \(\frac{2001}{2002}< \frac{2002}{2002}=1;\frac{2005}{2003}>\frac{2003}{2003}=1\text{ hay }\frac{2001}{2002}< 1< \frac{2005}{2003}\)

Vậy \(\frac{2001}{2002}< \frac{2005}{2003}\).

e. \(-\frac{2005}{2010}< 0;\frac{2001}{2002}>0\text{ hay }-\frac{2005}{2010}< 0< \frac{2001}{2002}\)

Vậy \(-\frac{2005}{2010}< \frac{2001}{2002}\).

b. \(\frac{33}{131}>\frac{33}{132}=\frac{1}{4};\frac{53}{217}< \frac{53}{212}=\frac{1}{4}\text{ hay }\frac{53}{217}< \frac{1}{4}< \frac{33}{131}\)

Vậy \(\frac{53}{217}< \frac{33}{131}\).

a) ta thay 1-2002/2003= 1/2003 va 1-2003/2004=1/2004 

ma 1/2003>1/2004 =>2002/2003<2003/2004

b) ta co -2002/2003<1<2005/2004

a.2002/2003<2003/2004

b.-2002/2003<2005/-2004

neu dung thi ?

a.<;b.<

=1+1/2001+1+1/2002+1+1/2003+...+1+1/2008=8+1/2001+1/2002+1/2003+...+1/2008>8

\(\frac{2002}{2001}+\frac{2003}{2002}+\frac{2004}{2003}+\frac{2005}{2004}+\frac{2006}{2005}+\frac{2007}{2006}+\frac{2008}{2007}+\frac{2009}{2008}>8\)

Ta có:

2002/2001=1+1/2001

2003/2002=1+1/2002

2004/2003= 1+ 1/2003

2005/2004= 1+ 1/2004

2006/2005=1+ 1/2005

2007/2006= 1+ 1/2006

2008/2007=1 + 1/2007.

2009/2008=1+ 1/2008.

=> 2002/2001+2003/2002+2004?2003+2005/2004+2006/2005+ 2007/2006+ 2008/2007+ 2009/2008= 1+1+1+1+1+1+1+1+1/2001+1/2002+1/2003+1/2004+1/2005+1/2006+1/2007+1/2008>8.

Nhớ k đúng cho mình nha!! Thanks!!!

a) Ta có: \(1-\frac{2002}{2003}=\frac{1}{2003}\)

\(1-\frac{2003}{2004}=\frac{1}{2004}\)

Vì \(\frac{1}{2003}>\frac{1}{2004}\)

\(\Rightarrow\frac{2002}{2003}>\frac{2003}{2004}\)

b) Ta có: \(\frac{-2005}{-2004}=\frac{2005}{2004}>1\)

\(\frac{-2002}{2003}

Ta có :

\(\frac{-2002}{2003}>-1\)

\(-1>\frac{-2005}{2004}\)

\(\Rightarrow\frac{-2002}{2003}>\frac{-2005}{2004}\)

Ta có: 

\(-\frac{2002}{2003}>-1\)

\(-\frac{2005}{2004}< -1\)

=> \(-\frac{2002}{2003}>-\frac{2005}{2004}\)

Ta có :

\(\frac{-2002}{2003}>-1\)

\(\frac{-2005}{2004}< -1\)

\(\Rightarrow\frac{-2002}{2003}>\frac{-2005}{2004}\)