Câu 1. Với a là số tự nhiên khác 0. Khẳng định nào sau đây là sai:
A. am
+ an
= am + n B. am
. an
= am + n
C. am
: an
= am - n
, (m ≥ n) D. a0
= 1
Câu 1. Với a là số tự nhiên khác 0. Khẳng định nào sau đây là sai:
A. am
+ an
= am + n B. am
. an
= am + n
C. am
: an
= am - n
, (m ≥ n) D. a0
= 1
Câu 1. Với a là số tự nhiên khác 0. Khẳng định nào sau đây là sai:
A. am
+ an
= am + n B. am
. an
= am + n
C. am
: an
= am - n
, (m ≥ n) D. a0
= 1
Trong các khẳng định sau, khẳng định nào đúng, khẳng định nào sai?
a) Với số thực a và các số nguyên m, n, ta có:
am.an=am.n;aman=am−nam.an=am.n;aman=am−n
b) Với hai số thực a, b cùng khác 0 và số nguyên n, ta có:
(ab)n=an.bn;(ab)n=anbn(ab)n=an.bn;(ab)n=anbn
c) Với hai số thực a, b thỏa mãn 0 < a < b với số nguyên a, ta có an < bn
d) Với số thực a khác 0 và hai số nguyên m, n, ta có: Nếu m>n thì am>an
(am là a mũ m,an là amux n nha giúp mik )
Cho tam giác ABC đều với M; N ; P lần lượt là trung điểm của BC; CA; AB. Khẳng định nào sau đây đúng?
A. AM → + BN → + CP → = 0 →
B. MA → + BN → + CP → = 0 →
C. AM → + BN → = CP →
D. BN → + PC → = AM →
Chọn khẳng định SAI trong các khẳng định sau nếu A và B đối xương với nhau qua trung điểm của đoạn thẳng MN thì
A. M,N đối xừng với nhau qua trung điểm AB
B. Tứ giác AMBN là hình bình hành
C. AM//BM VÀ AM=BN
D. AB=MN
Mình cần gấp ạk
Cho tam giác ABC đều . 2 điểm M,N di động trên 2 cạnh AB,AC sao cho AM/BM+AN/NC=1. CMR
1,MN^2=AM^2-AM.AN+AN^2
2,MN luôn tiếp xúc với 1 đtr cố định khi M,N di động trên cạnh AB,AC mà vẫn thỏa mãn yêu cầu để bài cho
Cho đoạn thẳng AB có trung điểm I . Gọi M là trung điểm đoạn IB. Khẳng định nào sau đây đúng? A. Vectơ AM - 3 vectơ BM = vectơ 0 B. Vectơ AM + 3 vectơ MB = vectơ 0 C. Vectơ MA +3 vectơ BM = vectơ 0 D. Vectơ AM + 3 vectơ BM = vectơ 0 ( Giải chi tiết giúp mình ạ )
ta có: I là trung điểm của AB
=>\(IA=IB=\dfrac{AB}{2}\)
M là trung điểm của IB
=>\(MI=MB=\dfrac{IB}{2}=\dfrac{AB}{4}\)
AM=AI+IM=1/2AB+1/4AB=3/4AB
=>AM=MB
=>\(\overrightarrow{AM}=3\overrightarrow{MB}\)
=>\(\overrightarrow{AM}-3\overrightarrow{MB}=\overrightarrow{0}\)
=>\(\overrightarrow{AM}+3\overrightarrow{BM}=\overrightarrow{0}\)
=>Chọn C
Cho đường tròn (O; 6cm) . Gọi A là điểm nằm ngoài đường tròn sao cho OA = 10cm.
Qua A dựng hai tiếp tuyến AM và AN đến (O), với M và N là tiếp điểm. Gọi giao điểm của AO và MN là H. Tìm khẳng định đúng?
A. OH = 3,6cm
B. AH = 4,8cm
C. MH = 6,4 cm
D.Tất cả sai
Đáp án A
Theo tính chất hai tiếp tuyến cắt nhau ta có: OH là đường phân giác của góc MON
Tam giác MON có OM = ON (= R) nên đây là tam giác cân tại O có OH là đường phân giác nên đồng thời là đường cao.
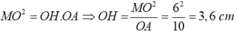
AH = AO – OH = 10 – 3,6 = 6,4 cm
Xét tam giác AMO vuông tại M có MH là đường cao.Áp dụng hệ thức cạnh và góc trong tam giác vuông ta có:
M H 2 = OH.AH = 3,6.6,4 = 23,04 ⇒ MH = 4,8cm
Cho hàm số f(n)= a n + 1 + b n + 2 + c n + 3 ( n ∈ N * ) với a, b, c là hằng số thỏa mãn a+b+c=0. Khẳng định nào sau đây đúng?
A. lim x → + ∞ f ( n ) = - 1
B. lim x → + ∞ f ( n ) = 1
C. lim x → + ∞ f ( n ) = 0
D. lim x → + ∞ f ( n ) = 2
Cho đường tròn tâm O nội tiếp tam giác đều ABC, 1 tiếp tuyến của đường tròn cắt cạnh AB,AC ở M,N.
a, CMR: MN^2 = AM^2 + AN^2 - AM.AN
b, CMr
AM/MB + AN/NC = 1