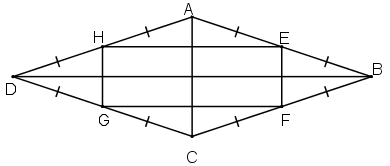
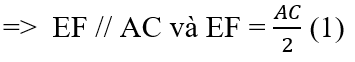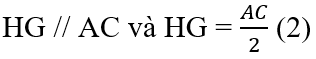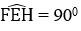Chứng minh rằng các trung điểm của bốn cạnh trong một hình chữ nhật là các đỉnh của một hình thoi.

Những câu hỏi liên quan
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi
Tham khảo: https://loigiaihay.com/bai-75-trang-106-sgk-toan-8-tap-1-c43a3348.html
Đúng 0
Bình luận (0)
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
* Tương tự tam giác ADC có HG là đường trung bình nên:
Từ (1) và (2) suy ra: EF // HG và EF = HG
=> tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên
Hình bình hành EFGH có Ê = 90º nên là hình chữ nhật
Đúng 0
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.
Tham kho dưới đây nhé
https://loigiaihay.com/bai-75-trang-106-sgk-toan-8-tap-1-c43a3348.html
Đúng 0
Bình luận (0)
Xét hcn ABCD có M,N,P,Q là trung điểm AB,BC,CD,DA
Ta thấy MN,PQ lần lượt là đường trung bình tam giác ABC và ACD
Suy ra MN//AC;\(MN=\dfrac{1}{2}AC\) và PQ//AC;\(PQ=\dfrac{1}{2}AC\)
Do đó MN//PQ và MN=PQ
Hay MNPQ là hbh
Lại có NP là đtb tg BCD nên \(NP=\dfrac{1}{2}BD\)
Mà ABCD là hcn nên \(NP=\dfrac{1}{2}BD=\dfrac{1}{2}AC=MN\)
Vậy MNPQ là hthoi (đpcm)
Đúng 1
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi.
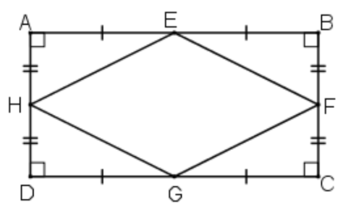
* Xét tam giác ABD có E và H lần lượt là trung điểm của AB và AD
=> EH là đường trung bình của tam giác
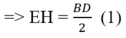
* Chứng minh tương tự, ta có:
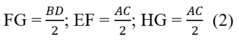
* Lại có, ABCD là hình chữ nhật nên AC = BD (3)
Từ (1), (2), (3) suy ra: EF = FG = GH= HE
=> tứ giác EFGH là hình thoi.
Đúng 0
Bình luận (0)
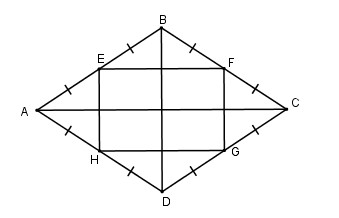
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
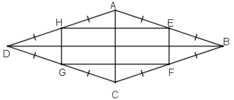
* Xét tam giác ABC có E và F lần lượt là trung điểm của AB và BC
=> EF là đường trung bình của tam giác ABC
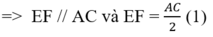
* Tương tự tam giác ADC có HG là đường trung bình nên:
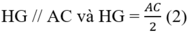
Từ (1) và (2) suy ra: EF // HG và EF = HG
=> tứ giác EFGH là hình bình hành.
Lại có: EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
Nên 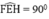
Hình bình hành EFGH có Ê = 90º nên là hình chữ nhật
Đúng 0
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh một hình thoi là các đỉnh của một hình chữ nhật ?
Bài giải:
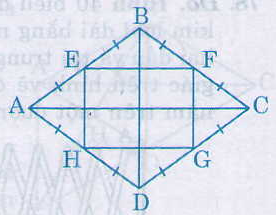
Ta có: EB = EA, FB = FA (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
HD = HA, GD = GC (gt)
nên HG là đường trung bình của ∆ADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FC (2)
Từ (1) (2) ta được EFGH là hình bình hành.
Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
nên ˆFEHFEH^ = 900
Hình bình hành EFGH có ˆEE^ = 900 nên là hình chữ nhật.
Đúng 0
Bình luận (1)
Bài giải:

Ta có: EB = EA, FB = FA (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
HD = HA, GD = GC (gt)
nên HG là đường trung bình của ∆ADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FC (2)
Từ (1) (2) ta được EFGH là hình bình hành.
Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
nên ˆFEHFEH^ = 900
Hình bình hành EFGH có ˆEE^ = 900 nên là hình chữ nhật.
Đúng 0
Bình luận (1)
Bài giải:
Ta có: EB=EA,FB=FAEB=EA,FB=FA (gt)
nên EFEF là đường trung bình của ΔABC∆ABC.
Do đó EF//ACEF//AC
HD=HA,GD=GCHD=HA,GD=GC (gt)
nên HGHG là đường trung bình của ΔADC∆ADC.
Do đó HG//ACHG//AC
Suy ra EF//HGEF//HG (1)
Chứng minh tương tự EH//FGEH//FG (2)
Từ (1) (2) ta được EFGHEFGH là hình bình hành.
Lại có EF//ACEF//AC và BD⊥ACBD⊥AC nên BD⊥EFBD⊥EF
EH//BDEH//BD và EF⊥BDEF⊥BD nên EF⊥EHEF⊥EH
nên ˆFEH=900FEH^=900
Hình bình hành EFGHEFGH có ˆE=900E^=900 nên là hình chữ nhật.
![]()
Đúng 0
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của một hình thoi ?
Bài giải:
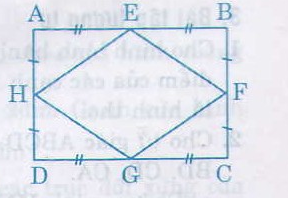
Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( = 1212AB = 1212CD)
HA = FB = DH = CF
( = 1212AD = 1212BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
Đúng 0
Bình luận (0)

Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( = 12AB = 12CD)
HA = FB = DH = CF
( = 12AD = 12BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
Đúng 0
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh của một hình thoi là các đỉnh của một hình chữ nhật.
Ta có: EB = EA, FB = FA (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
HD = HA, GD = GC (gt)
nên HG là đường trung bình của ∆ADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FC (2)
Từ (1) (2) ta được EFGH là hình bình hành.
Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
nên FEH = 900
Hình bình hành EFGH có E = 900 nên là hình chữ nhật.
Đúng 0
Bình luận (0)
Ta có: EB = EA, FB = FA (gt)
nên EF là đường trung bình của ∆ABC.
Do đó EF // AC
HD = HA, GD = GC (gt)
nên HG là đường trung bình của ∆ADC.
Do đó HG // AC
Suy ra EF // HG (1)
Chứng minh tương tự EH // FC (2)
Từ (1) (2) ta được EFGH là hình bình hành.
Lại có EF // AC và BD ⊥ AC nên BD ⊥ EF
EH // BD và EF ⊥ BD nên EF ⊥ EH
nên FEH = 900
Hình bình hành EFGH có E = 900 nên là hình chữ nhật.
ai tích mình tích lại
Đúng 0
Bình luận (0)
cái này hok từ đời nào òi bn dảnh ghê nhưng mk sẽ kick vì bn đã từng tl câu hỏi của mk hihihihi
Đúng 0
Bình luận (0)
Chứng minh rằng các trung điểm của bốn cạnh của một hình chữ nhật là các đỉnh của hình thoi.
Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( 1/2 = AB = 1/2 CD)
HA = FB = DH = CF
( = 1/2AD =1/2 BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
Đúng 0
Bình luận (0)
Bốn tam giác vuông EAH, EBF, GDH, GCF có:
AE = BE = DG = CG
( 1/2 = AB = 1/2 CD)
HA = FB = DH = CF
( = 1/2AD =1/2 BC)
Nên ∆EAH = ∆EBF = ∆GDH = ∆GCF (c.g.c)
Suy ra EH = EF = GH = GF
Vậy EFGH là hình thoi (theo định nghĩa)
ai tích mình tích lại
Đúng 0
Bình luận (0)
Chứng minh rằng trung điểm bốn cạnh của một hình chữ nhật là đỉnh của một hình thoi ?