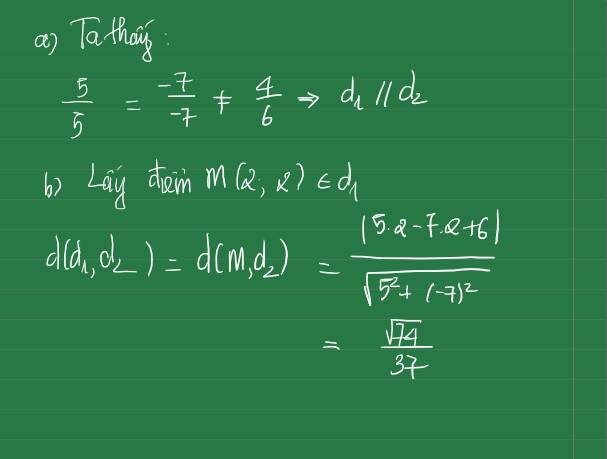Xét vị trí tương đối của hai đường thẳng y = -5x và y = -5x + 2.

Những câu hỏi liên quan
cho đường thẳng d1 : y = -2x+3 d2: y = -2x + m d3 : y = 1/2 x + 1 a) xét vị trí tương đối của hai đường thẳng d1 và d2 b) xét vị trí tương đối của hai đường thẳng d2 và d3
d1//d2 vì chung hệ số của x là -2
d2 cắt d3 do các hệ số a,b đều khác nhau
Đúng 1
Bình luận (0)
Cho 2 đường thẳng d1: 5x-7y+4=0; d2: 5x-7y+6=0 a)Xét vị trí tương đối của d1 và d2 b) tính d(d1;d2)
Xét vị trí tương đối của cặp đường thẳng \({d_1}\)và \({d_2}\)sau đây:
a) \({d_1}:x - y + 2 = 0\) và \({d_2}:x + y + 4 = 0\)
b) \({d_1}:\left\{ \begin{array}{l}x = 1 + 2t\\y = 3 + 5t\end{array} \right.\) và \({d_2}:5x - 2y + 9 = 0\)
c) \({d_1}:\left\{ \begin{array}{l}x = 2 - t\\y = 5 + 3t\end{array} \right.\) và \({d_2}:3x + y - 11 = 0\)
a) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {1; - 1} \right),\overrightarrow {{n_2}} = \left( {1;1} \right)\)
Ta có \(\overrightarrow {{n_1}} .\overrightarrow {{n_2}} = 1.1 + ( - 1).1 = 0\) nên \(\overrightarrow {{n_1}} \bot \overrightarrow {{n_2}} \)
Giải hệ phương trình \(\left\{ \begin{array}{l}x - y + 2 = 0\\x + y + 4 = 0\end{array} \right.\) ta được nghiệm \(\left\{ \begin{array}{l}x = - 3\\y = - 1\end{array} \right.\)
Suy ra hai đường thẳng \({d_1}\)và \({d_2}\) vuông góc và cắt nhau tại \(M\left( { - 3; - 1} \right)\)
b) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {5; - 2} \right),\overrightarrow {{n_2}} = \left( {5; - 2} \right)\)
\(\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} \) trùng nhau nên hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(1;3)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(5.1 - 2.3 + 9 = 8 \ne 0\), suy ra A không thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) song song
c) \({d_1}\)và \({d_2}\) có vectơ pháp tuyến lần lượt là \(\overrightarrow {{n_1}} = \left( {3;1} \right),\overrightarrow {{n_2}} = \left( {3;1} \right)\)
Suy ra hai vectơ pháp tuyến cùng phương. Suy ra \({d_1}\)và \({d_2}\)song song hoặc trùng nhau
Lấy điểm \(A(2;5)\) thuộc \({d_1}\), thay tọa độ của A vào phương trình \({d_2}\), ta được \(3.2 + 5 - 11 = 0\), suy ra A thuộc đường thẳng \({d_2}\)
Vậy hai đường thẳng \({d_1}\)và \({d_2}\) trùng nhau
Đúng 0
Bình luận (0)
d1 : y=-2x+3 , d2: y= -2x+m và d3; y=\(\dfrac{1}{2}x+1\)
Xét vị trí tương đối của hai đường thẳng:
a) d1 và d2 b) d2 và d3
Cho hai đường thẳng
∆
:
x
-
1
2
y
+
3
1
z
-...
Đọc tiếp
Cho hai đường thẳng
∆ : x - 1 2 = y + 3 1 = z - 4 - 2 ∆ ' : x + 2 - 4 = y - 1 - 2 = z + 1 4
Xét vị trí tương đối giữa ∆ và ∆ ′
∆ đi qua điểm M 0 (1; -3; 4) và có vecto chỉ phương a → = (2; 1; −2)
∆ ′ đi qua điểm M 0 ’ (-2; 1; -1) và có vecto chỉ phương a → = (−4; −2; 4)
Ta có: 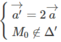
Vậy ∆ ′ song song với ∆
Đúng 0
Bình luận (0)
Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng
∆
1
:
x
-
1
2
y
+
1
2
z
3
;
∆
2
:
...
Đọc tiếp
Trong không gian tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 2 = y + 1 2 = z 3 ; ∆ 2 : x - 3 - 1 = y - 3 - 2 = z + 2 1
A. ∆ 1 song song với ∆ 2 .
B. ∆ 1 chéo với ∆ 2 .
C. ∆ 1 cắt ∆ 2 .
D. ∆ 1 trùng với ∆ 2 .
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng
∆
1
:
x
-
1
1
y
2
z
-
3
-
1
và
∆
2
:
x
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau
Xét vị trí tương đối của hai đường thẳng \({\Delta _1}:\left\{ \begin{array}{l}x = 1 + {t_1}\\y = - 2 + {t_1}\end{array} \right.\) và \({\Delta _2}:\left\{ \begin{array}{l}x = 2{t_2}\\y = - 3 + 2{t_2}\end{array} \right.\)
Ta có: \(\overrightarrow {{u_1}} = \left( {1;1} \right),\overrightarrow {{u_2}} = \left( {2;2} \right)\). Ta thấy, \(\overrightarrow {{u_2}} = 2\overrightarrow {{u_1}} \).
Chọn điểm \(A\left( {1; - 2} \right) \in {\Delta _1}\). Thay tọa độ điểm A vào phương trình đường thẳng \({\Delta _2}\) ta được \({t_2} = \frac{1}{2} \Rightarrow A\left( {1; - 2} \right) \in {\Delta _2}\).
Vậy 2 đường thẳng \({\Delta _1}\) và \({\Delta _2}\) song song với nhau.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
d
1
:
x
-
1
2
y
1
z
+
2
-
2
,
d
2
:
x
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 1 2 = y 1 = z + 2 - 2 , d 2 : x + 2 - 2 = y - 1 - 1 = z 2 . Xét vị trí tương đối của hai đường thẳng đã cho.
A. Chéo nhau
B. Trùng nhau
C. Song song
D. Cắt nhau
Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
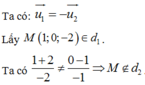
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C
Đúng 0
Bình luận (0)