Tính tích: \(\left( {3{\rm{x}}y} \right)\left( {x + y} \right)\)

Những câu hỏi liên quan
Tính:
\(\left( {3{{\rm{x}}^2}y + 5{\rm{x}}y - 2} \right)\left( {4{\rm{x}} + 3y} \right) - 6{{\rm{x}}^2}\left( {2{\rm{x}}y + \frac{3}{2}{y^2} + \frac{{10}}{3}y} \right)\)
Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.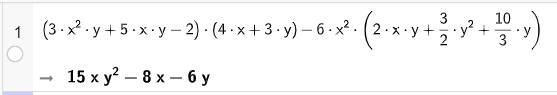
Đúng 0
Bình luận (0)
a) Rút gọn rồi tính giá trị biểu thức:
\(P = \left( {5{{\rm{x}}^2} - 2{\rm{x}}y + {y^2}} \right) - \left( {{x^2} + {y^2}} \right) - \left( {4{{\rm{x}}^2} - 5{\rm{x}}y + 1} \right)\) khi x = 1,2 và x + y = 6,2
b) Chứng minh giá trị của biểu thức sau không phụ thuộc vào giá trị của biến a:
\(\left( {{x^2} - 5{\rm{x}} + 4} \right)\left( {2{\rm{x}} + 3} \right) - \left( {2{{\rm{x}}^2} - x - 10} \right)\left( {x - 3} \right)\)
a) Vì x = 1,2 và x + y = 6,2 nên \(y = 6,2 - x = 6,2 - 1,2 = 5\)
\(\begin{array}{l}P = \left( {5{{\rm{x}}^2} - 2{\rm{x}}y + {y^2}} \right) - \left( {{x^2} + {y^2}} \right) - \left( {4{{\rm{x}}^2} - 5{\rm{x}}y + 1} \right)\\P = 5{{\rm{x}}^2} - 2{\rm{x}}y + {y^2} - {x^2} - {y^2} - 4{{\rm{x}}^2} + 5{\rm{x}}y - 1\\P = \left( {5{{\rm{x}}^2} - {x^2} - 4{{\rm{x}}^2}} \right) + \left( {{y^2} - {y^2}} \right) + \left( { - 2{\rm{x}}y + 5{\rm{x}}y} \right)\\P = 3{\rm{x}}y - 1 \end{array}\)
Thay x = 1,2; y = 5 vào biểu thức P = 3xy - 1 ta được
\(P = 3.1,2.5 - 1 = 17\)
Vậy P = 17
Đúng 0
Bình luận (0)
b) Ta có:
\(\begin{array}{l}\left( {{x^2} - 5{\rm{x}} + 4} \right)\left( {2{\rm{x}} + 3} \right) - \left( {2{{\rm{x}}^2} - x - 10} \right)\left( {x - 3} \right)\\ = {x^2}.2{\rm{x}} + {x^2}.3 - 5{\rm{x}}.2{\rm{x}} - 5{\rm{x}}.3 + 4.2{\rm{x}} + 4.3 - {\rm{[2}}{{\rm{x}}^2}.x + 2{{\rm{x}}^2}.( - 3) - x.x - x.( - 3) - 10.x - 10.( - 3){\rm{]}}\\ = 2{{\rm{x}}^3} + 3{{\rm{x}}^2} - 10{{\rm{x}}^2} - 15{\rm{x}} + 8{\rm{x}} + 12 - 2{{\rm{x}}^3} + 6{\rm{x}}{}^2 + {x^2} - 3{\rm{x}} + 10{\rm{x}} - 30\\ = \left( {2{{\rm{x}}^3} - 2{{\rm{x}}^3}} \right) + \left( {3{{\rm{x}}^2} - 10{{\rm{x}}^2} + 6{{\rm{x}}^2} + {x^2}} \right) + ( - 15{\rm{x}} + 8{\rm{x}} - 3{\rm{x}} + 10{\rm{x}}) +(12-30)\\ = - 18\end{array}\)
Vậy biểu thức đã cho bằng -18 nên không phụ thuộc vào biến x
Đúng 0
Bình luận (0)
Tìm thương và dư (nếu có) trong các phép chia sau:
\(\begin{array}{l}a)\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\\b)\left( {2{{\rm{x}}^3} + 5{{\rm{x}}^2} - 2{\rm{x}} + 12} \right):\left( {2{{\rm{x}}^2} - x + 1} \right)\end{array}\)
a) Tìm thương và dư (nếu có) trong các phép chia \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right):\left( {3{{\rm{x}}^2}y} \right)\)
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.
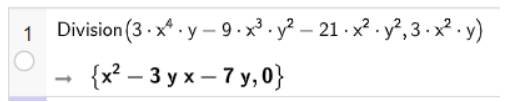
Vậy phép chia hai đa thức \(\left( {3{{\rm{x}}^4}y - 9{{\rm{x}}^3}{y^2} - 21{{\rm{x}}^2}{y^2}} \right)\) cho \(3{{\rm{x}}^2}y\), ta được thương là \({x^2} - 3{\rm{x}}y - 7y\) và dư 0.
b) Tìm thương và dư (nếu có) trong các phép chia (2x3 + 5x2 – 2x + 12) : (2x2 – x + 1).
• Sử dụng lệnh Division(<đa thức bị chia>, <đa thức chia>) để tìm thương và dư của phép chia hai đa thức.
• Nhập biểu thức trên dòng lệnh của cửa sổ CAS sau đó nhấn Enter, kết quả sẽ được hiển thị ngay bên dưới.

Vậy phép chia hai đa thức (2x3 + 5x2 – 2x + 12) cho (2x2 – x + 1), ta được thương là x + 3 và dư 9.
Đúng 0
Bình luận (0)
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:a) A 0,2left( {5{rm{x}} - 1} right) - dfrac{1}{2}left( {dfrac{2}{3}x + 4} right) + dfrac{2}{3}left( {3 - x} right)b) B left( {x - 2y} right)left( {{x^2} + 2{rm{x}}y + 4{y^2}} right) - left( {{x^3} - 8{y^3} + 10} right)c) C 4{left( {x + 1} right)^2} + {left( {2{rm{x}} - 1} right)^2} - 8left( {x - 1} right)left( {x + 1} right) - 4{rm{x}}
Đọc tiếp
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:
a) \(A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\)
b) \(B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\)
c) \(C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\)
a)
\(\begin{array}{l}A = 0,2\left( {5{\rm{x}} - 1} \right) - \dfrac{1}{2}\left( {\dfrac{2}{3}x + 4} \right) + \dfrac{2}{3}\left( {3 - x} \right)\\A = x - 0,2 - \dfrac{1}{3}x - 2 + 2 - \dfrac{2}{3}x\\ = \left( {x - \dfrac{1}{3}x - \dfrac{2}{3}x} \right) + \left( {\dfrac{{ - 1}}{2} - 2 + 2} \right)\\ = - \dfrac{1}{2}\end{array}\)
Vậy \(A = - \dfrac{1}{2}\) không phụ thuộc vào biến x
b)
\(\begin{array}{l}B = \left( {x - 2y} \right)\left( {{x^2} + 2{\rm{x}}y + 4{y^2}} \right) - \left( {{x^3} - 8{y^3} + 10} \right)\\B = \left[ {x - {{\left( {2y} \right)}^3}} \right] - {x^3} + 8{y^3} - 10\\B = {x^3} - 8{y^3} - {x^3} + 8{y^3} - 10 = - 10\end{array}\)
Vậy B = -10 không phụ thuộc vào biến x, y.
c)
\(\begin{array}{l}C = 4{\left( {x + 1} \right)^2} + {\left( {2{\rm{x}} - 1} \right)^2} - 8\left( {x - 1} \right)\left( {x + 1} \right) - 4{\rm{x}}\\{\rm{C = 4}}\left( {{x^2} + 2{\rm{x}} + 1} \right) + \left( {4{{\rm{x}}^2} - 4{\rm{x}} + 1} \right) - 8\left( {{x^2} - 1} \right) - 4{\rm{x}}\\C = 4{{\rm{x}}^2} + 8{\rm{x}} + 4 + 4{{\rm{x}}^2} - 4{\rm{x}} + 1 - 8{{\rm{x}}^2} + 8 - 4{\rm{x}}\\C = \left( {4{{\rm{x}}^2} + 4{{\rm{x}}^2} - 8{{\rm{x}}^2}} \right) + \left( {8{\rm{x}} - 4{\rm{x}} - 4{\rm{x}}} \right) + \left( {4 + 1 + 8} \right)\\C = 13\end{array}\)
Vậy C = 13 không phụ thuộc vào biến x
Đúng 0
Bình luận (0)
Tính tổng: \(\frac{5}{{2{{\rm{x}}^2}\left( {6{\rm{x}} + y} \right)}} + \frac{3}{{5{\rm{x}}y\left( {6{\rm{x}} + y} \right)}}\)
Ta có: \(\frac{5}{{2{{\rm{x}}^2}\left( {6{\rm{x}} + y} \right)}} + \frac{3}{{5{\rm{x}}y\left( {6{\rm{x}} + y} \right)}} = \frac{{25y}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}} + \frac{{6{\rm{x}}}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}} = \frac{{25y + 6{\rm{x}}}}{{10{{\rm{x}}^2}y\left( {6{\rm{x}} + y} \right)}}\)
Đúng 0
Bình luận (0)
Thực hiện phép tính:a) left( { - xy} right)left( { - 2{{rm{x}}^2}y + 3{rm{x}}y - 7{rm{x}}} right) b) left( {dfrac{1}{6}{x^2}{y^2}} right)left( { - 0,3{{rm{x}}^2}y - 0,4{rm{x}}y + 1} right)c) left( {x + y} right)left( {{x^2} + 2{rm{x}}y + {y^2}} right) d) left( {x - y} right)left( {{x^2} - 2{rm{x}}y + {y^2}} right)
Đọc tiếp
Thực hiện phép tính:
a) \(\left( { - xy} \right)\left( { - 2{{\rm{x}}^2}y + 3{\rm{x}}y - 7{\rm{x}}} \right)\) b) \(\left( {\dfrac{1}{6}{x^2}{y^2}} \right)\left( { - 0,3{{\rm{x}}^2}y - 0,4{\rm{x}}y + 1} \right)\)
c) \(\left( {x + y} \right)\left( {{x^2} + 2{\rm{x}}y + {y^2}} \right)\) d) \(\left( {x - y} \right)\left( {{x^2} - 2{\rm{x}}y + {y^2}} \right)\)
a)
\(\begin{array}{l}\left( { - xy} \right)\left( { - 2{{\rm{x}}^2}y + 3{\rm{x}}y - 7{\rm{x}}} \right)\\ = \left( { - xy} \right).\left( { - 2{{\rm{x}}^2}y} \right) + \left( { - xy} \right)\left( {3{\rm{x}}y} \right) + \left( { - xy} \right).\left( { - 7{\rm{x}}} \right)\\ = 2{{\rm{x}}^3}{y^2} - 3{{\rm{x}}^2}{y^2} + 7{{\rm{x}}^2}y\end{array}\)
b)
\(\begin{array}{l}\left( {\dfrac{1}{6}{x^2}{y^2}} \right)\left( { - 0,3{{\rm{x}}^2}y - 0,4{\rm{x}}y + 1} \right)\\ = \left( {\dfrac{1}{6}{x^2}{y^2}} \right).\left( { - 0,3{{\rm{x}}^2}y} \right) + \left( {\dfrac{1}{6}{x^2}{y^2}} \right).\left( { - 0,4{\rm{x}}y} \right) + \left( {\dfrac{1}{6}{x^2}{y^2}} \right).1\\ = - \dfrac{1}{{20}}{x^4}{y^3} - \dfrac{1}{{15}}{x^3}{y^3} + \dfrac{1}{6}{x^2}{y^2}\end{array}\)
Đúng 0
Bình luận (0)
c)
\(\begin{array}{l}\left( {x + y} \right)\left( {{x^2} + 2{\rm{x}}y + {y^2}} \right)\\ = x.{x^2} + x.2{\rm{x}}y + x.{y^2} + y.{x^2} + y.2{\rm{x}}y + y.{y^2}\\ = {x^3} + 2{{\rm{x}}^2}y + x{y^2} + {x^2}y + 2{\rm{x}}{y^2} + {y^3}\\ = {x^3} + 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} + {y^3}\end{array}\)
d)
\(\begin{array}{l}\left( {x - y} \right)\left( {{x^2} - 2{\rm{x}}y + {y^2}} \right)\\ = x.{x^2} + x.\left( { - 2{\rm{x}}y} \right) + x.{y^2} + \left( { - y} \right).{x^2} + \left( { - y} \right).\left( { - 2{\rm{x}}y} \right) + \left( { - y} \right).{y^2}\\ = {x^3} - 2{{\rm{x}}^2}y + x{y^2} - {x^2}y + 2{\rm{x}}{y^2} - {y^3}\\ = {x^3} - 3{{\rm{x}}^2}y + 3{\rm{x}}{y^2} - {y^3}\end{array}\)
Đúng 0
Bình luận (0)
Khẳng định sau đúng hay sai? Vì sao?
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Khẳng định trên là đúng. Vì nhân cả tử và mẫu của phân thức \(\frac{{2y}}{{3\left( {x - y} \right)}}\) với 15 ta được phân thức
\(\frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} \Rightarrow \frac{{30{\rm{x}}{y^2}\left( {x - y} \right)}}{{45{\rm{x}}y{{\left( {x - y} \right)}^2}}} = \frac{{2y}}{{3\left( {x - y} \right)}}\)
Đúng 0
Bình luận (0)
Khẳng định trên là đúng vì :
\(\dfrac{30xy^2\left(x-y\right)}{45xy\left(x-y\right)^2}\\ =\dfrac{30xy^2\left(x-y\right):15xy\left(x-y\right)}{45xy\left(x-y\right)^2:15xy\left(x-y\right)}\\ =\dfrac{2y}{3\left(x-y\right)}\left(dpcm\right)\)
Đúng 0
Bình luận (0)
Rút gọn biểu thức:
\(a)\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\)
b) \(\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\)
c) \(\left( {4{\rm{x}} - 1} \right)\left( {6y + 1} \right) - 3{\rm{x}}\left( {8y + \dfrac{4}{3}} \right)\)
d) \(\left( {x + y} \right)\left( {x - y} \right) + \left( {x{y^4} - {x^3}{y^2}} \right):\left( {x{y^2}} \right)\)
a)
\(\begin{array}{l}\left( {x - y} \right)\left( {{x^2} + xy + {y^2}} \right)\\ = x.{x^2} + x.xy + x.{y^2} - y.{x^2} - y.xy - y.{y^2}\\ = {x^3} + {x^2}y + x{y^2} - {x^2}y - x{y^2} - {y^3}\\ = {x^3} - {y^3}\end{array}\)
b)
\(\begin{array}{l}\left( {x + y} \right)\left( {{x^2} - xy + {y^2}} \right)\\ = x.{x^2} + x.\left( { - xy} \right) + x{y^2} + y.{x^2} + y.\left( { - xy} \right) + y.{y^2}\\ = {x^3} - {x^2}y + x{y^2} + {x^2}y - x{y^2} + {y^3}\\ = {x^3} + {y^3}\end{array}\)
Đúng 0
Bình luận (0)
c)
\(\begin{array}{l}\left( {4{\rm{x}} - 1} \right)\left( {6y + 1} \right) - 3{\rm{x}}\left( {8y + \dfrac{4}{3}} \right)\\ = 4{\rm{x}}.6y + 4{\rm{x}}.1 - 1.6y - 1.1 - 3{\rm{x}}.8y - 3{\rm{x}}.\dfrac{4}{3}\\ = 24{\rm{x}}y + 4{\rm{x}} - 6y - 1 - 24{\rm{x}}y - 4{\rm{x}}\\ = - 6y - 1\end{array}\)
d)
\(\begin{array}{l}\left( {x + y} \right)\left( {x - y} \right) + \left( {x{y^4} - {x^3}{y^2}} \right):\left( {x{y^2}} \right)\\ = x.x + x.\left( { - y} \right) + y.x + y.\left( { - y} \right) + \left( {x{y^4}} \right):\left( {x{y^2}} \right) + \left( { - {x^3}{y^2}} \right):\left( {x{y^2}} \right)\\ = {x^2} - xy + xy - {y^2} + {y^2} - x^2\\ = 0\end{array}\)
Đúng 0
Bình luận (0)
Khẳng định nào sau đây là đúng:A. frac{{{{left( {x - 1} right)}^2}}}{{x - 2}} frac{{{{left( {1 - x} right)}^2}}}{{2 - x}}B. frac{{3{rm{x}}}}{{{{left( {x + 2} right)}^2}}} frac{{3{rm{x}}}}{{{{left( {x - 2} right)}^2}}}C. frac{{3{rm{x}}}}{{{{left( {x + 2} right)}^2}}} frac{{ - 3{rm{x}}}}{{{{left( {x - 2} right)}^2}}}D. frac{{3{rm{x}}}}{{{{left( {x + 2} right)}^2}}} frac{{3{rm{x}}}}{{{{left( { - x - 2} right)}^2}}}
Đọc tiếp
Khẳng định nào sau đây là đúng:
A. \(\frac{{{{\left( {x - 1} \right)}^2}}}{{x - 2}} = \frac{{{{\left( {1 - x} \right)}^2}}}{{2 - x}}\)
B. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\)
C. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{ - 3{\rm{x}}}}{{{{\left( {x - 2} \right)}^2}}}\)
D. \(\frac{{3{\rm{x}}}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{\rm{x}}}}{{{{\left( { - x - 2} \right)}^2}}}\)\(\)
Khẳng định `A` là đúng vì :
\(\dfrac{\left(x-1\right)^2}{x-2}\\ =\dfrac{\left(x-1\right)^2}{-\left(x-2\right)}\\ =\dfrac{\left(1-x\right)^2}{2-x}\)
`->` Đã là hằng đẳng thức mũ `2` thì `(x-1)^2=(1-x)^2`
Đúng 1
Bình luận (0)
D. 3x/(-x - 2)²
= 3x/[-(x + 2)]²
= 3x/(x + 2)²
Câu này mới đúng nhé Min
Đúng 0
Bình luận (0)
Cho: \(P = \left( {21{{\rm{x}}^4}{y^5}} \right):\left( {7{{\rm{x}}^3}{y^3}} \right)\). Tính giá trị của biểu thức P tại x = -0,5; y = 2.
Ta có: \(P = \left( {21{{\rm{x}}^4}{y^5}} \right):\left( {7{{\rm{x}}^3}{y^3}} \right) = \left( {21:7} \right).\left( {{x^4}:{x^3}} \right).\left( {{y^5}:{y^3}} \right) = 3{\rm{x}}{y^2}\)
Thay x = -0,5; y = 2 vào biểu thức \(P = 3{\rm{x}}{y^2}\) ta được:
\(P = 3.\left( { - 0,5} \right){.2^2} = - 6\)
Vậy P = -6 tại x = -0,5; y = 2
Đúng 0
Bình luận (0)








