Cho đường thẳng a song song với mặt phẳng left( P right), mặt phẳng left( Q right) chứa a và cắt left( P right) theo giao tuyến b (Hình 10). Trong left( Q right), hai đường thẳng a,b có bao nhiều điểm chung?Cho ba mặt phẳng song song left( P right),left( Q right),left( R right) lần lượt cắt hai đường thăng a và a tại các điểm A,B,C và A,B,C. Gọi {B_1} là giao điểm của AC với left( Q right) (Hình 12).a) Trong tam giác ACC, có nhận xét gì về mối liên hệ giữa frac{{AB}}{{BC}} và frac{{A{B_1}}}{{{B_...
Đọc tiếp
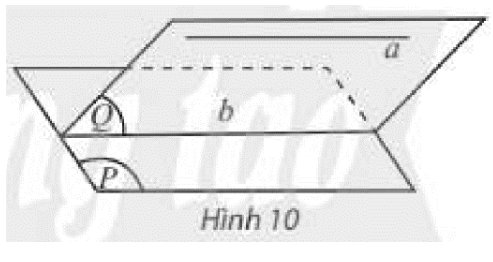
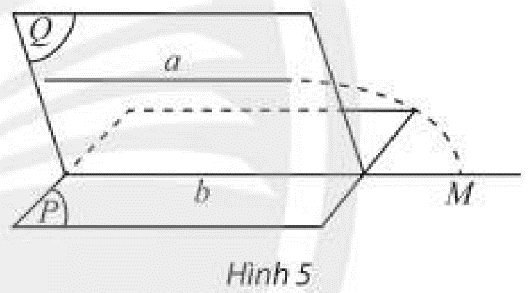
Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\), mặt phẳng \(\left( Q \right)\) chứa \(a\) và cắt \(\left( P \right)\) theo giao tuyến \(b\) (Hình 10). Trong \(\left( Q \right)\), hai đường thẳng \(a,b\) có bao nhiều điểm chung?
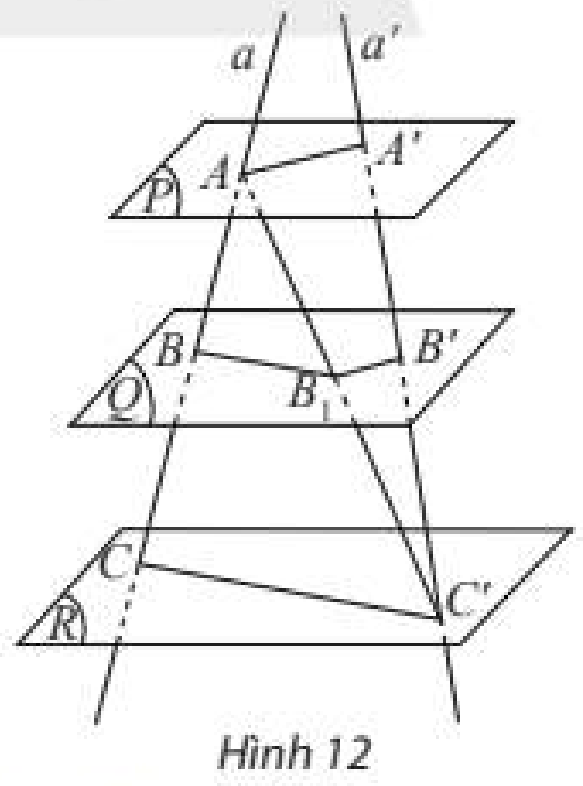
Cho ba mặt phẳng song song \(\left( P \right),\left( Q \right),\left( R \right)\) lần lượt cắt hai đường thăng \(a\) và \(a'\) tại các điểm \(A,B,C\) và \(A',B',C'\). Gọi \({B_1}\) là giao điểm của \(AC'\) với \(\left( Q \right)\) (Hình 12).
a) Trong tam giác \(ACC'\), có nhận xét gì về mối liên hệ giữa \(\frac{{AB}}{{BC}}\) và \(\frac{{A{B_1}}}{{{B_1}C'}}\)?
b) Trong tam giác \(AA'C'\), có nhận xét gì về mối liên hệ giữa \(\frac{{A{B_1}}}{{{B_1}C'}}\) và \(\frac{{A'B'}}{{B'C'}}\)?
c) Từ đó, nếu nhận xét về mối liên hệ giữa các tỉ số \(\frac{{AB}}{{A'B'}},\frac{{BC}}{{B'C'}},\frac{{AC}}{{A'C'}}\).