Đồ thị của các hàm số y=sinx và y=cosx cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn [−2π;`(5π)/2`]
?
A. 5 B. 6 C. 4 D. 7
Trên đoạn − 2 π ; 5 π 2 , đồ thị hai hàm số y = s inx và y = cos x cắt nhau tại bao nhiêu điểm?
A.2
B.4
C.3
D.5
Đáp án là D.
Xét phương trình hoành độ giao điểm sin x = cos x ⇔ sin x − cos x = 0 ∗
Số giao điểm của hai đồ thị hàm số chính là số nghiệm của phương trình (*) trên − 2 π ; 5 π 2 .
Khi đó ta có sin x − cos x = 0 ⇔ 2 sin x − π 4 = 0 ⇔ x = π 4 + k π , k ∈ ℤ .
Mà x ∈ − 2 π ; 5 π 2 nên ta có − 2 π ≤ π 4 + k π ≤ 5 π 2 − 2 π ≤ π 4 + k π ≤ 5 π 2 .
Hay ta có k ∈ − 2 ; − 1 ; 0 ; 1 ; 2 .
Trên đoạn - 2 π ; 5 π 2 , đồ thị hai hàm số y=sinx và y=cosx cắt nhau tại bao nhiêu điểm?
A. 2
B. 3
C. 5
D. 8
Chọn C
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: sinx = cosx

Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn - 2 π ; 5 π 2
Đồ thị của các hàm số \(y = \sin x\) và \(y = \cos x\) cắt nhau tại bao nhiêu điểm có hoành độ thuộc đoạn \(\left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\)?
A. 5 B. 6 C. 4 D. 7
Phương trình hoàn độ giao điểm của hai đồ thì hàm số là \(\sin x = \cos x\)
\( \Leftrightarrow \tan x = 1 \Leftrightarrow x = \frac{\pi }{4} + k\pi \;\left( {k \in \mathbb{Z}} \right)\)
Do \(x \in \left[ { - 2\pi ;\frac{{5\pi }}{2}} \right]\; \Leftrightarrow - 2\pi \le \frac{\pi }{4} + k\pi \le \frac{{5\pi }}{2}\;\; \Leftrightarrow \; - \frac{9}{4} \le k \le \frac{9}{4}\;\;\;\)
Mà \(k\; \in \mathbb{Z}\;\; \Leftrightarrow k\; \in \left\{ { - 2;\; - 1;0;1;2} \right\}\)
Vậy ta chọn đáp án A
Tìm hoành độ các điểm cực đại x C Đ ; hoành độ các điểm cực tiểu x C T của đồ thị hàm số y=sinx+cosx
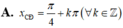
![]()
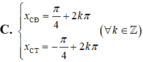
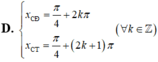
Trên đoạn - 2 π , 5 π 2 , đồ thị hai hàm số y = sin x và y = cos x cắt nhau tại bao nhiêu điểm?
A. 2
B. 4
C. 3
D. 5
Cho hàm số y = x 3 - 3 m x 2 + 6 m x - 8 có đồ thị (C). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 5 ; 5 để (C) cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số nhân?
A. 8
B. 7
C. 9
D. 11
Cho hàm số y = x 3 - 3 m x 2 + 6 m x - 8 có đồ thị (C). Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-5;5] để (C) cắt trục hoành tại ba điểm phân biệt có hoành độ lập thành cấp số nhân
A. 8
B. 7
C. 9
D. 11
Cho hàm số y = a x 3 + b x 2 + c x + d có đạo hàm là hàm số y=f'(x) có đồ thị như hình vẽ bên.
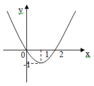
Biết rằng đồ thị hàm số y=f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y=f(x) cắt trục tung tại điểm có tung độ bằng bao nhiêu?
A. 2 3
B. 1
C. 3 2
D. 4 3
Đáp án D
Ta có: y ' = 3 a x 2 + 2 b x + c
+) Đồ thị hàm số f'(x) đi qua gốc tọa độ => c=0
+) Đồ thị hàm số f'(x) có điểm cực trị:
1 ; − 1 ⇒ 6 a + 2 b = 0 3 a + 2 b = − 1 ⇔ a = 1 3 b = − 1
Vậy hàm số f ' x = x 2 − 2 x . Đồ thị hàm số f(x) tiếp xúc với trục hoành nên có cực trị nằm trên trục hoành. Các giá trị cực trị của hàm số f(x) là:
f 0 = d f 2 = 8 3 − 4 + d = − 4 3 + d
do điểm tiếp xúc có hoành độ dương
=> d = 4 3 => f(x) cắt trục tung tại điểm có tung độ 4 3
Cho hàm số y = ax 3 + bx 2 + cx + d có đạo hàm là hàm số y = f '(x) có đồ thị như hình vẽ bên. Biết rằng đồ thị hàm số y = f(x) tiếp xúc với trục hoành tại điểm có hoành độ dương. Hỏi đồ thị hàm số y = f(x)cắt trục tung tại điểm có tung độ bằng bao nhiêu?
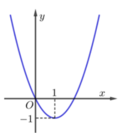
A. 2 3 .
B. 1
C. 3 2 .
D. 4 3 .