cho tam giác MNP vuông tại M có MN=5cm , NP=13 . MI là đường cao.Tính NI,MI

Những câu hỏi liên quan
cho tam giác MNP vuông tại M . MN = 4cm, MP = 3cm. đường cao MI : a) Cm tam giác MNP và tam giác INM đồng dang => MN mũ 2 = NP . NI; b) tính độ dài NI và IP : c) gọi NE là tia phân giác của góc MNP . K là giao điểm NE và MI. cm EM/EP, NI/MN ; d) kẻ IH vuong góc với MN tại H. tính diện tích tam giác IMH
Cho tam giác MNP vuông tại M có đường cao MI chia cạnh huyền NP thành hai đoạn NI = 5cm và IP = 7cm
a Tính độ dài các đoạn MI, MN, NP
b Gọi K là trung tâm của NP. Tính số đo góc MKN (làm tròn đến độ )
c Kẻ MH vuông góc với NK (H thuộc NK). CM : NH.NK = NI.NP
a: NP=NI+IP
=5+7=12(cm)
Xét ΔMNP vuông tại M có MI là đường cao
nên \(\left\{{}\begin{matrix}MN^2=NI\cdot NP\\MP^2=PK\cdot PN\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}MN=\sqrt{5\cdot12}=2\sqrt{15}\left(cm\right)\\MP=\sqrt{7\cdot12}=2\sqrt{21}\left(cm\right)\end{matrix}\right.\)
b: trung tâm là cái gì vậy bạn?
c: Nếu kẻ như thế thì H trùng với I rồi bạn
Đúng 1
Bình luận (1)
Cho tam giác MNP vuông tại M có đường cao MI chia cạnh huyền NP thành hai đoạn NI = 5cm và IP = 7cm
a Tính độ dài các đoạn MI, MN, NP
b Gọi K là trung tâm của MP. Tính số đo góc MKN (làm tròn đến độ )
c Kẻ MH vuông góc với NK (H thuộc NK). CM : NH.NK = NI.NP
(Vẽ giúp mình cái hình cảm ơn)
A áp dụng hệ thức lượng trong tam giác....
+ MI=NI*IP
MI=5*7
MI=35
BC=NI+IP
BC=5+7=12
+ MN=NP*NI
MN= 12*5=60
Đúng 0
Bình luận (0)
cho tam giác MNP cân tại M Vẽ mi vuông góc với NP tại I
Chứng minh MI là đường trung trực của N P
vẽ IE vuông góc với MN tại A, IB vuông góc với MP tại B chứng minh tam giác IAB cân
Giả sử góc MNP = 45° MN = 2 cm Tính NP
Giả sử góc MNP = 30 độ Chứng minh tam giác AIB đều
Cho tam giác MNP ( góc M= 90°), MH vuông góc với NP tại H, MN=9, MP=12. a, chứng minh tam giác HNM đồng dạng vs tam giác MNP b, tính NP, MH, NH, HP c, gọi MI là phân giác góc M. Tính NI, IP
a, xét tam giá HNM và tam giác MNP có chung :
góc MNP
cạnh MN
cạnh NI của tam giác HNM nằm trên cạnh NP của tam giác MNP
=> tam giác HNM đồng dạng MNP (c-g-c)
b,
áp dụng đ/l pytago vào tam giác vuông MNP :
=>NP=15cm
MH.NP =NM.MP
MH.15=9.12
=>MH=7,2cm
áp dụng đl pytago vào tam giác vuông MNH ( NHM = 90\(^o\)):
=>NH=5,4cm
HP=NP-NH
HP=15-5,4=9,6cm
c,
vì MI là phân giác của góc M
=> MI là trung tuyến của tam giác MNP nên:
NI=IP
mà NI+IP=15cm
=> NI=IP =7,5cm
Đúng 0
Bình luận (0)
Cho tam giác MNP có I là trung điểm NP. MI là phân giác, G là trọng tâm của tam giác MNP. NK vuông góc với MP tại K. O là giao điểm của NK và MI.
a) Chứng minh tam giác MNP cân tại M
b) NP= 16, MG= 4. Tính MI và MN
c) CO vuông góc với MN
ta cso:

Cho ∆MNP vuông tại M có MN< MP. Kẻ đường phân giác NI của góc MNP ( I thuộc MP) .kẻ IK vuông góc NP a. Chứng minh rằng ∆IMN=∆IKN b. chứng minh rằng MI < IP c. Gọi Q là giao điểm của IK và MN , đường thẳng NI cắt QP tại D. Chứng minh rằng ND vuông góc QP
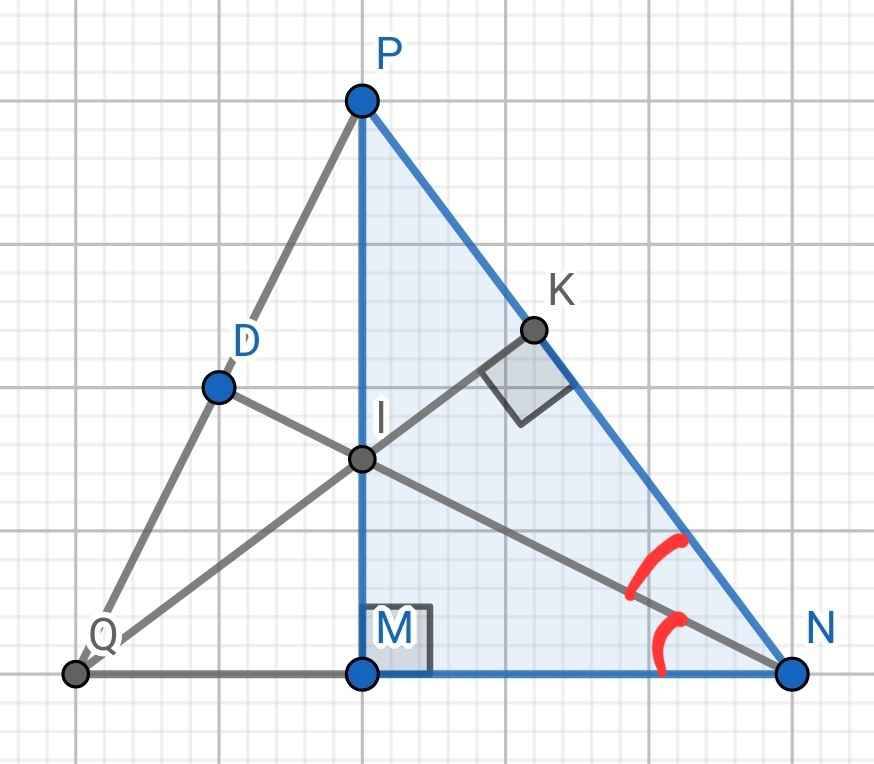
a) Xét hai tam giác vuông: ∆IMN và ∆IKN có:
IN chung
MNI = KNI (do NI là phân giác của ∠MNP)
⇒ ∆IMN = ∆IKN (cạnh huyền - góc nhọn)
b) ∆IKP vuông tại K
IP là cạnh huyền nên IP lớn nhất
IK < IP (1)
Do ∆IMN = ∆IKN (cmt)
⇒ MI = IK (2)
Từ (1) và (2)⇒ MI < IP
c) Xét hai tam giác vuông: ∆IKP và ∆IMQ có:
IM = IK (cmt)
∠PIK = ∠MIQ (đối đỉnh)
∆IKP = ∆IMQ (cạnh góc vuông - góc nhọn kề)
⇒ KP = MQ (hai cạnh tương ứng) (3)
Do ∆IMN = ∆IKN (cmt)
⇒ MN = KN (hai cạnh tương ứng) (4)
Từ (3) và (4) ⇒ KN + KP = MN + MQ
NP = NQ
⇒ ∆NPQ cân tại N
Lại có NI là phân giác của ∠MNP
⇒ NI là phân giác của ∠QNP
⇒ NI cũng là đường cao của ∆NPQ (tính chất tam giác cân)
⇒ ND ⊥ QP
Đúng 2
Bình luận (1)
Cho tam giác vuông MNP vuông tại M. Đường cao MI cắt cạnh NP thành hai đoạn là NI=4, IP=9
A, Tính MN, MP, MI, góc N, góc P.
B, Vẽ phân giác NK. Tính MK và KP.
C, Gọi G là giao điểm của NK và MI. Cm tam giác MGK cân.
Cho tam giác MNP có MN = 6 cm , NP = 8 cm và NP = 10 cm. Kẻ đường cao MI, gọi K là trung ddirrm của MI, A là trung điểm của NI. C/m:
a) AK vuông góc với MP, PK vuông góc với AM
b) Gọi E là trung điểm của IP. C/m tam giác AKE vuông


















