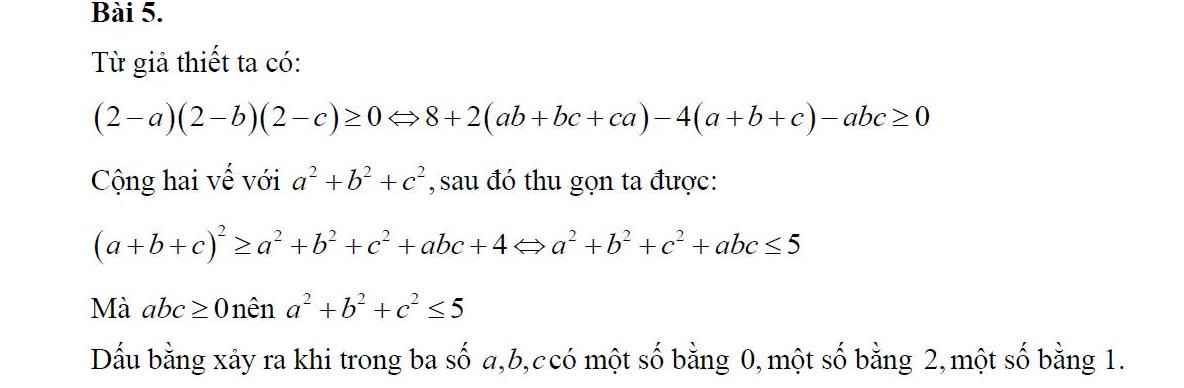Cho 2 số thực a,b thỏa mãn điểu kiện \(a^2+b^2\le2\).CMR \(a+b\le2\)

Những câu hỏi liên quan
Cho các số thực a,b,c thỏa mãn: \(-1\le a\le2;-1\le b\le2;-1\le c\le2\) và \(a+b+c=0\)
Chứng minh \(a^2+b^2+c^2\le6\)
\(-1\le a\le2\Rightarrow\hept{\begin{cases}a+1\ge0\\a-2\le0\end{cases}\Rightarrow\left(a+1\right)\left(a-2\right)\le0}\)
Tương tự \(\left(b+1\right)\left(b-2\right)\le0,\left(c+1\right)\left(c-2\right)\le0\)
=> (a+1)(a-2)+(b+1)(b-2)+(c+1)(c-2)\(\le\)0 => a2+b2+c2-(a+b+c)-6\(\le\)0
=>a2+b2+c2 \(\le\)6
Dấu "=" xảy ra <=> (a+1)( a-2)=0, (b+1)(b-2)=0, (c+1)(c-2)=0 , a+b+c=0 <=> a=2, b=c=-1 và các hoán vị
Đúng 0
Bình luận (0)
Cho các số thực dương a,b thỏa mãn \(\dfrac{a}{a^3+b}+\dfrac{b}{a+b^3}\ge1\). Chứng minh rằng:
\(a^2+b^2\le2\)
Cho a, b, c với \(-1\le a,b,c\le2\) thỏa mãn điều kiện \(a^2+b^2+c^2=6\). CMR \(a+b+c\ge0\)
Cho a, b, c là các số thực thỏa mãn \(a^2+b^2+c^2\le2\).
Tìm giá trị nhỏ nhất của biểu thức P = 2023ca - ab - bc.
Cho a,b là 2 số thực không âm thỏa mãn: \(a+b\le2\). Chứng minh:\(\dfrac{2+a}{1+a}+\dfrac{1-2b}{1+2b}\ge\dfrac{8}{7}\)
\(VT=1+\dfrac{1}{1+a}+\dfrac{2}{1+2b}-1=2\left(\dfrac{1}{2+2a}+\dfrac{1}{1+2b}\right)\)
\(VT\ge\dfrac{8}{3+2\left(a+b\right)}\ge\dfrac{8}{3+2.2}=\dfrac{8}{7}\)
Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}a=\dfrac{3}{4}\\b=\dfrac{5}{4}\end{matrix}\right.\)
Đúng 4
Bình luận (0)
CHo hai số thực a,b thỏa mãn \(1\le a\le2,1\le b\le2\). Tìm GTLN và CTNN của \(P=\left(a+\dfrac{2}{b}\right)\left(b+\dfrac{2}{a}\right)\)
Ta có: \(P=ab+\dfrac{4}{ab}+4\ge2\sqrt{ab.\dfrac{4}{ab}+4}=8\)
Dấu '=' xảy ra <=> \(\left\{{}\begin{matrix}ab=2\\1\le a,b\le2\end{matrix}\right.\)
Lại có: \(1\le a\le2,1\le b\le2\)
\(\Rightarrow1\le ab\le4\Leftrightarrow\left(ab-1\right)\left(ab-4\right)\le0\Leftrightarrow\left(ab\right)^2\le5ab-4\)
\(\Rightarrow P=\dfrac{\left(ab\right)^2+4ab+4}{ab}\le\dfrac{5ab-4+4ab+4}{ab}=9\)
Dấu '=' xảy ra <=> \(\left[{}\begin{matrix}ab=1\\ab=4\end{matrix}\right.\) và \(1\le a,b\le2\) \(\Leftrightarrow\left[{}\begin{matrix}a=b=2\\a=b=1\end{matrix}\right.\)
Vậy \(Min_P=8\Leftrightarrow ab=2;1\le a,b\le2\)
\(Max_P=9\Leftrightarrow\left[{}\begin{matrix}a=b=1\\a=b=2\end{matrix}\right.\)
Đúng 2
Bình luận (0)
Cho các số thực a , b , c thỏa mãn điều kiện : \(0\le a,b,c\le2\) và a+b+c = 3
Tìm GTNN và GTLN của biểu thức P = \(\frac{a^2+b^2+c^2}{ab+bc+ca}\)
đặt \(t=ab+bc+ca\)
\(=>t=ab+bc+ca\le\frac{1}{3}\left(a+b+c\right)^2=3\)
mặt khác
\(\left(a+b+c\right)^2=a^2+b^2+c^2+2\left(ab+bc+ca\right)\)
\(=>a^2+b^2+c^2=9-2\left(ab+bc+ca\right)\)
khi đó
\(P=\frac{9-2t}{t}\)(zới t nhỏ hơn hoặc = 3)
xét \(f\left(t\right)=\frac{9-2t}{t}\left(t\le3\right)\)
\(f'\left(t\right)=-\frac{9}{t^2}< 0\)
=> f(t) N Biến \(\left(-\infty,3\right)\)
min f(t)=f(3)=1
koo tồn tại max\(f\left(t\right)\)
zậy minP=1 khi a=b=c=1
Cho 3 số a, b, c không âm thỏa mãn điều kiện a+b+c=2, chứng minh rằng: \(\dfrac{\sqrt{a}}{1+a}+\dfrac{\sqrt{b}}{1+a+b}+\dfrac{\sqrt{c}}{1+a+b+c}\le2\)
B1: Cho 0le a,b,cle2 thỏa mãn a+b+c3. CMR: a^2+b^2+c^2le5B2: Cho a,bge0 thỏa mãn a^2+b^2a+b. TÌm GTLN Sdfrac{a}{a+1}+dfrac{b}{b+1}B3: CMR: dfrac{1}{left(x-yright)^2}+dfrac{1}{x^2}+dfrac{1}{y^2}gedfrac{4}{xy}forall xne y,xyne0
Đọc tiếp
B1: Cho \(0\le a,b,c\le2\) thỏa mãn \(a+b+c=3\). CMR: \(a^2+b^2+c^2\le5\)
B2: Cho \(a,b\ge0\) thỏa mãn \(a^2+b^2=a+b\). TÌm GTLN \(S=\dfrac{a}{a+1}+\dfrac{b}{b+1}\)
B3: CMR: \(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\forall x\ne y,xy\ne0\)
Bài 3:
\(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\ge\dfrac{4}{xy}\)
\(\Leftrightarrow x^2y^2\left(\dfrac{1}{\left(x-y\right)^2}+\dfrac{1}{x^2}+\dfrac{1}{y^2}\right)\ge\dfrac{4}{xy}.x^2y^2\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2+y^2\ge4xy\)
\(\Leftrightarrow\dfrac{x^2y^2}{\left(x-y\right)^2}+x^2-2xy+y^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2+\left(x-y\right)^2\ge2xy\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}\right)^2-2xy+\left(x-y\right)^2\ge0\)
\(\Leftrightarrow\left(\dfrac{xy}{x-y}-x+y\right)^2=0\) (luôn đúng)
Đúng 4
Bình luận (4)