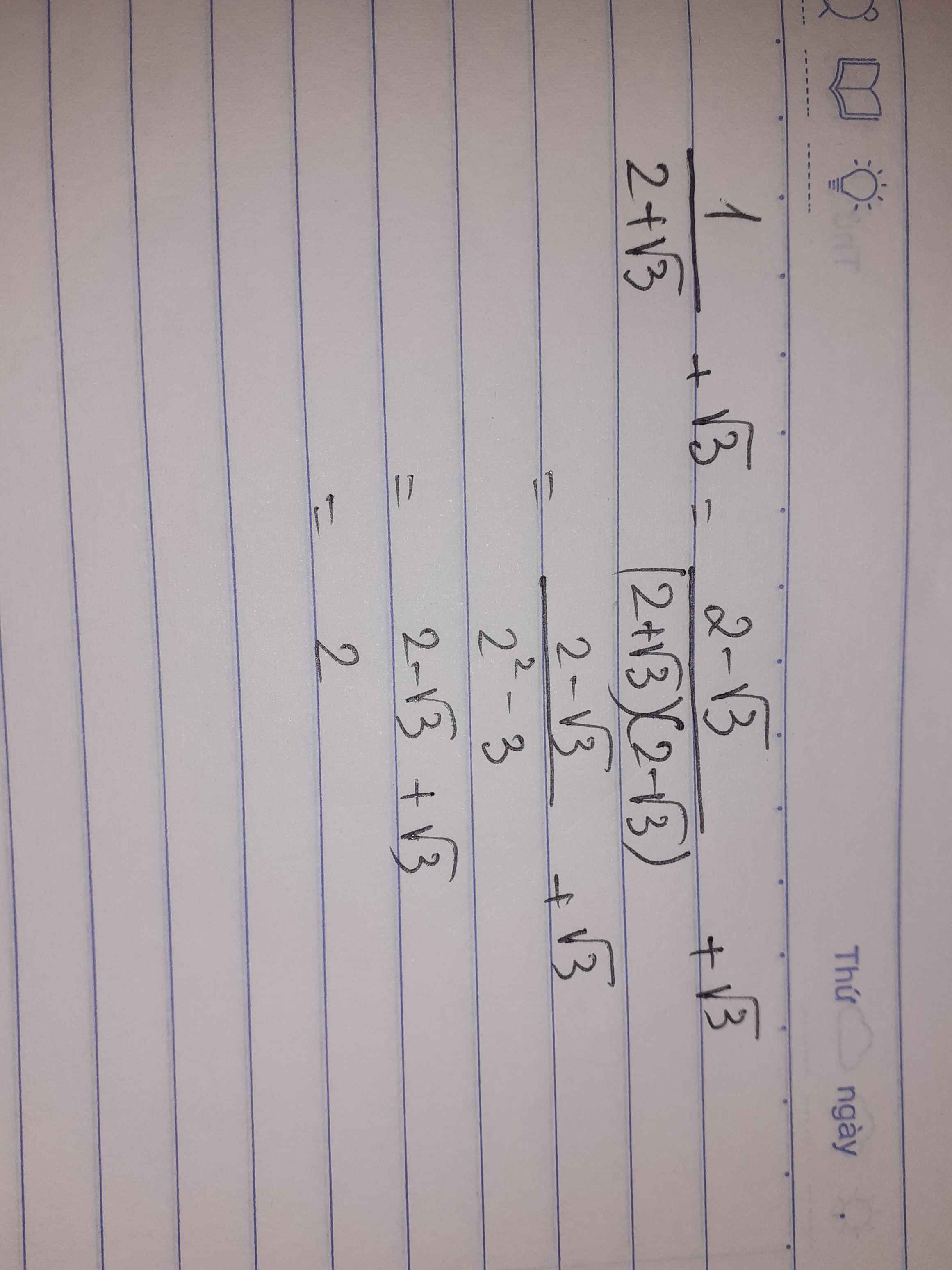Ta có: \(\dfrac{2\sqrt{3}}{\sqrt{3}+\sqrt{2}}+\sqrt{24}\)

\(=2\sqrt{3}\left(\sqrt{3}-\sqrt{2}\right)+2\sqrt{6}\)

\(=6-2\sqrt{6}+2\sqrt{6}\)

=6

\(A=\frac{3}{2+\sqrt{3}}+\frac{13}{4-\sqrt{3}}+\frac{6}{\sqrt{3}}\)

\(=\frac{3\left(2-\sqrt{3}\right)}{\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)}+\frac{13\left(4+\sqrt{3}\right)}{\left(4-\sqrt{3}\right)\left(4+\sqrt{3}\right)}+\frac{6}{\sqrt{3}}\)

\(=6-3\sqrt{3}+4+\sqrt{3}+\frac{6}{\sqrt{3}}\)

\(=10-2\sqrt{3}+\frac{6}{\sqrt{3}}\)

\(=\frac{10\sqrt{3}-6+6\sqrt{3}}{\sqrt{3}}\)

\(=\frac{16\sqrt{3}-6}{\sqrt{3}}\)

Ta có: \(\dfrac{1}{2+\sqrt{3}}+\sqrt{3}\)

\(=2-\sqrt{3}+\sqrt{3}\)

=2

\(\dfrac{6}{\sqrt{2}-\sqrt{3}+3}\)

\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{\left(\sqrt{2}-\sqrt{3}\right)^2-9}\)

\(=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}\)

\(=\dfrac{-3\left(\sqrt{2}-\sqrt{3}-3\right)}{2+\sqrt{6}}=\dfrac{-3\left(\sqrt{6}-2\right)\left(\sqrt{2}-\sqrt{3}-3\right)}{2}\)

Ta có: \(\dfrac{\sqrt{8-2\sqrt{12}}}{\sqrt{3}-1}\)

\(=\dfrac{\sqrt{\left(\sqrt{6}-\sqrt{2}\right)^2}}{\sqrt{3}-1}\)

\(=\sqrt{2}\)

tìm cả đk giúp mik vs

ĐKXĐ: \(x>0;x\ne1\)

\(A=\left(\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{2\left(\sqrt{x}+1\right)}{x\left(\sqrt{x}+1\right)}-\dfrac{2-x}{x\left(\sqrt{x}+1\right)}\right)\)

\(=\left(\dfrac{x+2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{x+2\sqrt{x}}{x\left(\sqrt{x}+1\right)}\right)\)

\(=\dfrac{\left(x+2\sqrt{x}\right).x.\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+2\sqrt{x}\right)}=\dfrac{x}{\sqrt{x}-1}\)

b.

\(x=4+2\sqrt{3}=\left(\sqrt{3}+1\right)^2\Rightarrow\sqrt{x}=\sqrt{3}+1\)

\(\Rightarrow A=\dfrac{4+2\sqrt{3}}{\sqrt{3}+1-1}=\dfrac{4+2\sqrt{3}}{\sqrt{3}}=\dfrac{6+4\sqrt{3}}{3}\)

c.

Để \(\sqrt{A}\) xác định \(\Rightarrow\sqrt{x}-1>0\Rightarrow x>1\)

Ta có:

\(\sqrt{A}=\sqrt{\dfrac{x}{\sqrt{x}-1}}=\sqrt{\dfrac{x}{\sqrt{x}-1}-4+4}=\sqrt{\dfrac{\left(\sqrt{x}-2\right)^2}{\sqrt{x}-1}+4}\ge\sqrt{4}=2\)

Dấu "=" xảy ra khi \(\sqrt{x}-2=0\Rightarrow x=4\)

Sửa đề : 

\(P=\sqrt{x+5+2\sqrt{x+4}}-\sqrt{x+5-2\sqrt{x+4}}\)\(\left(x\ge-4\right)\)

\(=\sqrt{\left(x+4\right)+2\sqrt{x+4}+1}-\sqrt{\left(x+4\right)-2\sqrt{x+4}+1}\)

\(=\sqrt{\left(\sqrt{x+4}+1\right)^2}-\sqrt{\left(\sqrt{x+4}-1\right)^2}\)

\(=\left|\sqrt{x+4}+1\right|-\left|\sqrt{x+4}-1\right|\)

\(=\sqrt{x+4}+1-\sqrt{x+4}+1=2\)

Vậy \(P=2\)

Tại sao lại phải sửa đề ạ?

Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{x+1}-\dfrac{4-3\sqrt{x}}{x-4\sqrt{x}+4}\right):\left(\dfrac{x-\sqrt{x}}{x\sqrt{x}-2x+\sqrt{x}-2}\right)\)

\(=\dfrac{\left(\sqrt{x}+1\right)\left(x-4\sqrt{x}+4\right)+\left(3\sqrt{x}-4\right)\left(x+1\right)}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}:\dfrac{x-\sqrt{x}}{\left(\sqrt{x}-2\right)\left(x+1\right)}\)

\(=\dfrac{x\sqrt{x}-4x+4\sqrt{x}+x-4\sqrt{x}+4+3x\sqrt{x}+3\sqrt{x}-4x-4}{\left(x+1\right)\left(\sqrt{x}-2\right)^2}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(x+1\right)}{x-\sqrt{x}}\)

\(=\dfrac{4x\sqrt{x}-7x+3\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\)

\(=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)\cdot\left(4\sqrt{x}-3\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}\)

\(=\dfrac{4\sqrt{x}-3}{\sqrt{x}-2}\)

Để A>1 thì A-1>0

\(\Leftrightarrow\dfrac{4\sqrt{x}-3-\sqrt{x}+2}{\sqrt{x}-2}>0\)

\(\Leftrightarrow\dfrac{3\sqrt{x}-1}{\sqrt{x}-2}>0\)

\(\Leftrightarrow\left[{}\begin{matrix}3\sqrt{x}-1\le0\\\sqrt{x}-2>0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}0< x\le\dfrac{1}{9}\\x>4\end{matrix}\right.\)