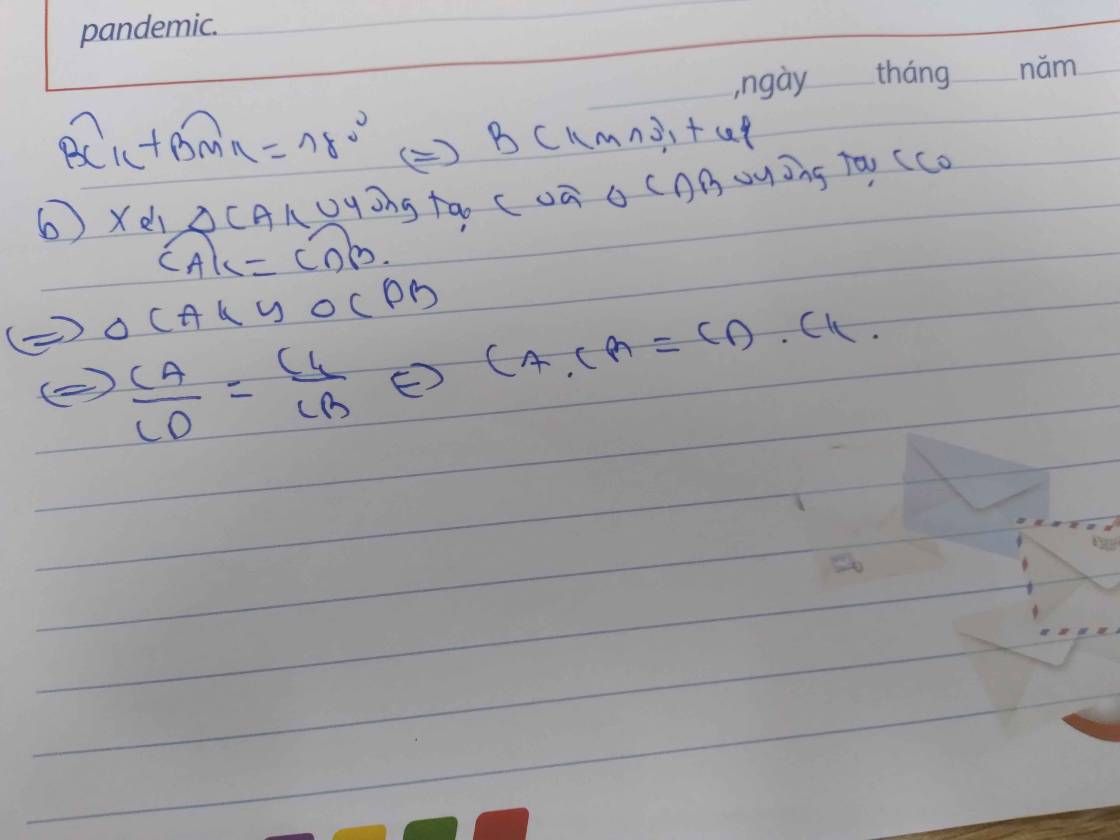Cho điểm A nằm trên nửa (O;R), đường kính BC. ( AB > AC ). Kẻ AH vuông góc với BC tại H. Gọ D, E là chân đường vuông góc từ H đến AB, AC.Gọi F là giao của DE với BC, K là giao của AF với (O). KE cắt BC tại M. CMR : \(MH^2=MC\cdot MF\)

Những câu hỏi liên quan
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh: 1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn. 2) CK.CD CA.CB 3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
Đọc tiếp
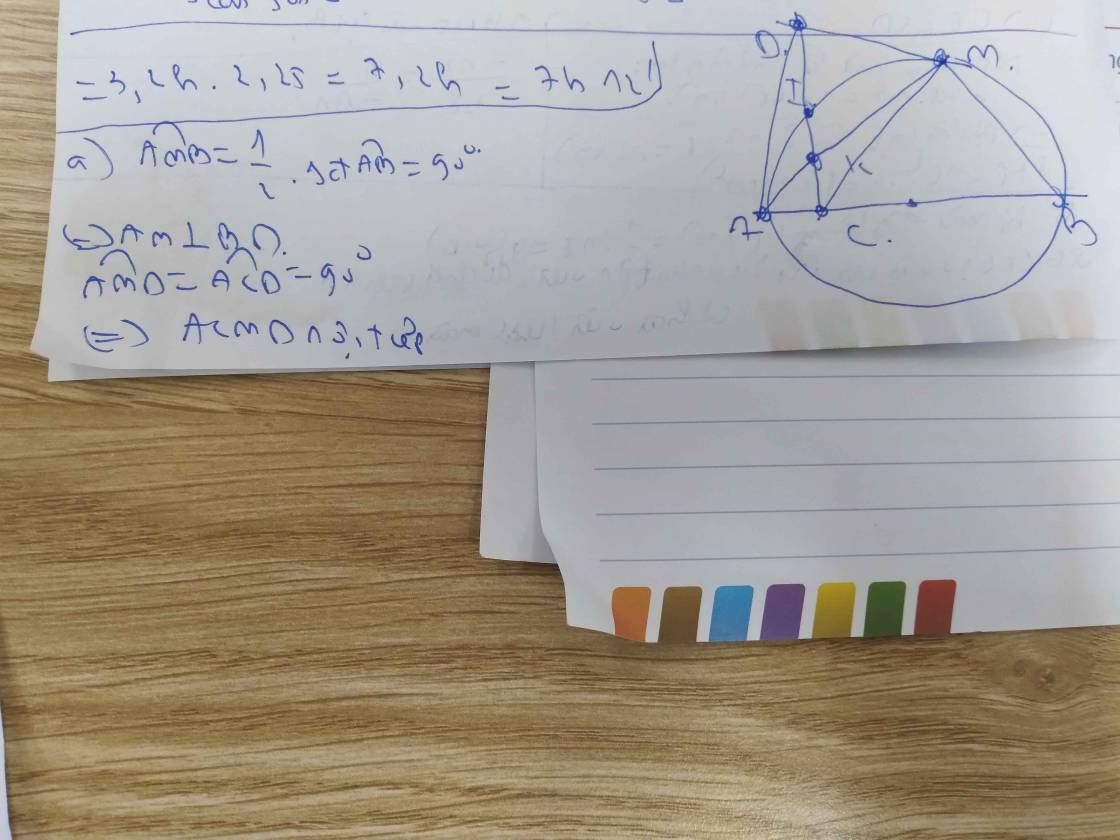
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.
2) CK.CD = CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Cho nửa (O) đường kính AB=2R,C lad điểm bất kì nằm trên nửa đường tròn sao cho C khác A và AC
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CDCA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB ,C là một điểm nằm giữa O và A .Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I ,K là một điểm nằm bất kì trên đoạn thẳng CI (K khác C và I) tia AK cắt nửa đường tròn O tại M tia BM cắt tia CI tại D .Chứng minh : a)Các tứ giác ACMD,BCKM nội tiếp đường tròn b)CK.CD=CA.CB c) Gọi N là giao điểm của AD và đường tròn O chứng minh B,K,N thẳng hàng
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
Đọc tiếp
cho nửa đường tròn (o; ab)c là điểm nằm giữa o và a ,đường thẳng vuông góc với ab . tại c cắt nửa đường tròn tại i , k là điểm bất kỳ nằm trên đoạn thẳng ci (k khác c và i) , tia ak cắt nửa đường tròn (o) tại m, tia bm cắt tia ci tại d. chứng minh: a, các tứ giác acmd, bckm nội tiếp đường tròn. b, ck.cd = ca.cb. c, gọi n là giao điểm của ad và đường tròn (o) chứng minh b,k,n thẳng hàng
a) Xét (O) có
ΔAMB nội tiếp đường tròn(A,M,B\(\in\)(O))
AB là đường kính(gt)
Do đó: ΔMAB vuông tại M(Định lí)
\(\Leftrightarrow AM\perp MB\) tại M
\(\Leftrightarrow AM\perp BD\) tại M
\(\Leftrightarrow\widehat{AMD}=90^0\)
Xét tứ giác ADMC có
\(\widehat{AMD}=\widehat{ACD}\left(=90^0\right)\)
\(\widehat{AMD}\) và \(\widehat{ACD}\) là hai góc cùng nhìn cạnh AD
Do đó: ADMC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
Đúng 0
Bình luận (0)
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định...
Đọc tiếp
Cho đường tròn tâm O điểm A nằm ngoài đường tròn. Vẽhai tiếp tuyến AM, AN với đường tròn tâm O ( M,N là hai tiếp điểm). Qua A vẽ 1 đường thẳng d cắt đường tròn tâm O tại B và C sao cho 2 điểm nằm giữa A và C, hai điểm O và N nằm trên hai nửa mặt phẳng đối nhau bên bờ là đường thẳng d. Đường thẳng MN cắt AO và AC lần lượt tại H và K.
a, Chứng minhAM bình = AH.AO
b, Gọi I là trung điểm của BC. Chứng minh góc AMK= góc AIN
c, Chứng minh rằng đường tròn ngoại tiếp tam giác OHK lun đi qua 1 điểm cố định khi đường tròn tâm O thay đổi nhưng lun đi qua điểm B và C cố định
Cho điểm C nằm trên nửa đường tròn tâm O đường kính AB 2R (C khác A và B). Gọi K là trung điểm của BC. Qua B vẽ tia tiếp tuyến Bx với nửa đường tròn tâm O (tia Bx và C nằm cùng một nửa mặt phẳng có bờ AB), Bx cắt tia OK tại D. a) Chứng minh ODC ODB, từ đó suy ra DC là tiếp tuyến của đường tròn tâm O. b) Chứng minh AC.OD 2R2 c) Vẽ CH vuông góc với AB tại H, gọi I là trung điểm của CH. Tiếp tuyến tại A của đường tròn tâm O cắt tia BI tại E. Chứng minh E, C, D thẳng hàng.
Đọc tiếp
Cho điểm C nằm trên nửa đường tròn tâm O đường kính AB = 2R (C khác A và B). Gọi K là trung điểm của BC. Qua B vẽ tia tiếp tuyến Bx với nửa đường tròn tâm O (tia Bx và C nằm cùng một nửa mặt phẳng có bờ AB), Bx cắt tia OK tại D. a) Chứng minh ODC = ODB, từ đó suy ra DC là tiếp tuyến của đường tròn tâm O. b) Chứng minh AC.OD = 2R2 c) Vẽ CH vuông góc với AB tại H, gọi I là trung điểm của CH. Tiếp tuyến tại A của đường tròn tâm O cắt tia BI tại E. Chứng minh E, C, D thẳng hàng.
Trên đường thẳng AM vẽ một điểm O(O nằm giữa A và M).Trên cùng một nửa mặt phẳng bờ AM vẽ các tia OB,OC sao cho : góc MOC115o ; góc BOC 70o.Trên nửa mặt phẳng đối diện dựng tia OD(D không cùng nằm trong nửa mặt phẳng với B,C qua bờ là AM) sao cho góc AOD45oa)Tia OB nằm giữa hai tia OM,OC không?Vì sao?b)Tính góc MOB và góc AOCc)Chứng tỏ rằng ba điểm D,O,B thẳng hàng
Đọc tiếp
Trên đường thẳng AM vẽ một điểm O(O nằm giữa A và M).Trên cùng một nửa mặt phẳng bờ AM vẽ các tia OB,OC sao cho : góc MOC=115o ; góc BOC = 70o.Trên nửa mặt phẳng đối diện dựng tia OD(D không cùng nằm trong nửa mặt phẳng với B,C qua bờ là AM) sao cho góc AOD=45o
a)Tia OB nằm giữa hai tia OM,OC không?Vì sao?
b)Tính góc MOB và góc AOC
c)Chứng tỏ rằng ba điểm D,O,B thẳng hàng
Cho đường tròn (O) bán kính R, một đường thẳng d không đi qua O cắt (O) tại A và B. Trên d lấy điểm C sao cho A nằm giữa C và B. Từ C kẻ hai tiếp tuyến CM; CN với (O) (M và N là 2 tiếp điểm sao cho M và O nằm trên cùng nửa mặt phẳng bờ chứa đường thẳng AB). a) Chứng minh : Bốn điểm C; M; O; N cùng thuộc một đường tròn. b) Chứng minh : CM2 CA. CB c) Đoạn CO cắt đoạn MN tại H. Chứng minh CH. CO CA. CB và góc CHA bằng góc OAB d) Đường thẳng vuông góc với CO tại O cắt các tia CM và CN thứ tự tại E...
Đọc tiếp
Cho đường tròn (O) bán kính R, một đường thẳng d không đi qua O cắt (O) tại A và B. Trên d lấy điểm C sao cho A nằm giữa C và B. Từ C kẻ hai tiếp tuyến CM; CN với (O) (M và N là 2 tiếp điểm sao cho M và O nằm trên cùng nửa mặt phẳng bờ chứa đường thẳng AB). a) Chứng minh : Bốn điểm C; M; O; N cùng thuộc một đường tròn. b) Chứng minh : CM2 = CA. CB c) Đoạn CO cắt đoạn MN tại H. Chứng minh CH. CO = CA. CB và góc CHA bằng góc OAB d) Đường thẳng vuông góc với CO tại O cắt các tia CM và CN thứ tự tại E và F. Xác định vị trí của C trên đường thẳng d để diện tích tam giác CEF nhỏ nhất.
a: Xét tứ giác CMON có \(\widehat{CMO}+\widehat{CNO}=90^0+90^0=180^0\)
nên CMON là tứ giác nội tiếp
=>C,M,O,N cùng thuộc một đường tròn
b: Xét (O) có
\(\widehat{CMA}\) là góc tạo bởi tiếp tuyến MC và dây cung MA
\(\widehat{ABM}\) là góc nội tiếp chắn cung AM
Do đó: \(\widehat{CMA}=\widehat{ABM}=\widehat{CBM}\)
Xét ΔCMA và ΔCBM có
\(\widehat{CMA}=\widehat{CBM}\)
\(\widehat{MCA}\) chung
Do đó: ΔCMA~ΔCBM
=>\(\dfrac{CM}{CB}=\dfrac{CA}{CM}\)
=>\(CM^2=CA\cdot CB\)
c: Xét (O) có
CM,CN là các tiếp tuyến
Do đó: CM=CN
=>C nằm trên đường trung trực của MN(1)
Ta có: OM=ON
=>O nằm trên đường trung trực của MN(2)
Từ (1),(2) suy ra OC là đường trung trực của MN
=>OC\(\perp\)MN tại H
Xét ΔCMO vuông tại M có MH là đường cao
nên \(CH\cdot CO=CM^2\)
=>\(CH\cdot CO=CA\cdot CB\)
=>\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
Xét ΔCHA và ΔCBO có
\(\dfrac{CH}{CB}=\dfrac{CA}{CO}\)
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCBO
=>\(\widehat{CHA}=\widehat{CBO}\)
mà \(\widehat{CBO}=\widehat{OAB}\)(ΔOAB cân tại O)
nên \(\widehat{CHA}=\widehat{OAB}\)
Đúng 0
Bình luận (0)
Trên đường thẳng AM. Lấy điểm O (O nằm giữa A và B ) Trên cùng nửa mặt phẳng vẽ các tia OB,OC.MOC=1150
BOC=700 Trên nửa mặt phẳng đối diện (D không nằm trong một nửa mặt phẳng BC) Qua B , Bù AM sao cho góc
OD=450.
a; Tia OB nằm giữa 2 tia OM và OC không?Vì sao?
b; Tính góc MOB , AOC
c; Chứng minh 3 điểm D,O,B thẳng hàng.