Tính đạo hàm của hàm số sau
y= cos^2021(x căn x)
Tính đạo hàm của hàm số sau
y = x cot 2x
Tính đạo hàm của hàm số y= căn cos(x²+2x+3)
Lời giải:
$y=\sqrt{\cos(x^2+2x+3)}$
$y'=\frac{-(x+1)\sin (x^2+2x+3)}{\sqrt{\cos (x^2+2x+3)}}$
Tính đạo hàm của hàm số y = cos2x . căn bậc hai của ( pi/4 - 2x)
Tính đạo hàm của hàm số sau y = sin x sin x - cos x
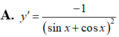
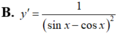
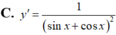

Tính đạo hàm của hàm số sau y = sin x sin x - cos x
![]()
![]()
![]()
![]()
Tính đạo hàm của hàm số y = sinx + cos x
A. sinx + cosx
B. sinx – cosx
C. cosx – sinx
D. - sinx – cosx
y ' = ( sin x + cos x ) ' y ' = ( sin x ) ' + ( cos x ) ' = c osx - sinx
Chọn đáp án C
Bằng cách viết \(y = \cos x = \sin \left( {\frac{\pi }{2} - x} \right),\) tính đạo hàm của hàm số \(y = \cos x.\)
\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)
Cách đạo hàm nhanh hs sau
y = \(\dfrac{x-m^2-m}{x+2}\)
\(y'=\dfrac{2-\left(-m^2-m\right)}{\left(x+2\right)^2}=\dfrac{m^2+m+2}{\left(x+2\right)^2}\)
Sử dụng công thức: \(\left(\dfrac{ax+b}{cx+d}\right)'=\dfrac{ad-bc}{\left(cx+d\right)^2}\)
Tính đạo hàm cấp hai của các hàm số sau:
a) \(y = {x^2} - x\);
b) \(y = \cos x\).
a: \(y'=\left(x^2-x\right)'=2x-1\)
\(y''=\left(2x-1\right)'=2\)
b: \(y'=\left(cosx\right)'=-sinx\)
\(y''=\left(-sinx\right)'=-cosx\)