Giải dùm pương trình này vs ạ
x(-2x+1)=-1

Những câu hỏi liên quan
B1. cho phương trình (x-1)^3-(a^2-a+7)(x-1)-3(a^2-a-2)=0
a, tìm các giá trị của a để một trong các nghiệm là 2
b, giải phương trình với các giá trị đó của a
B2.giải pương trình với tham số a
a, 4ax^3-12x^2-ax+3=0
b, 2a^2x^3+5a^2x^2-8x=20
Bài 2:
a: \(\Leftrightarrow4x^2\left(ax-3\right)-\left(ax-3\right)=0\)
\(\Leftrightarrow\left(ax-3\right)\left(2x-1\right)\left(2x+1\right)=0\)
Trường hợp 1: a=0
=>(2x-1)(2x+1)=0
=>x=1/2 hoặc x=-1/2
Trường hợp 2: a<>0
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-\dfrac{1}{2}\\x=\dfrac{3}{a}\end{matrix}\right.\)
b: \(\Leftrightarrow a^2x^2\left(2x+5\right)-4\left(2x+5\right)=0\)
\(\Leftrightarrow\left(2x+5\right)\left(a^2x^2-4\right)=0\)
Trường hợp 1: a=0
Phương trình sẽ là 2x+5=0
hay x=-5/2
Trường hợp 2: a<>0
Phương trình sẽ là \(\left(2x+5\right)\left[\left(ax\right)^2-4\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{5}{2}\\x=-\dfrac{2}{a}\\x=\dfrac{2}{a}\end{matrix}\right.\)
Đúng 2
Bình luận (0)
giải dùm mình phương trình sao:(2x+1)(x2 -1)=4x2-2x-2
Xem chi tiết
\(\left(2x+1\right)\left(x+1\right)\left(x-1\right)=4x^2-4x+2x-2\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=4x\left(x-1\right)+2\left(x-1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=\left(x-1\right)\left(4x+2\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)=2\left(x-1\right)\left(2x+1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x+1\right)\left(x-1\right)-2\left(x-1\right)\left(2x+1\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x-1\right)=0\)
\(\orbr{\begin{cases}2x+1=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{2}\\x=1\end{cases}}\)
Đúng 0
Bình luận (0)
pt\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1\right)=2\left(2x+1\right)\left(x-1\right)\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)\left(x+1-2\right)=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+1=0\\x-1=0\end{cases}}\)\(\Leftrightarrow\orbr{\begin{cases}x=-\frac{1}{2}\\x=1\end{cases}}\)
KL vậy....
Đúng 0
Bình luận (0)
Cám ơn 2 ng nhiều thank you so much
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
giúp dùm mình nha...
giải phương trình:
a) (x-2)^2-(x-3)(x+3)=6
b)4(x-3)^2-(2x-1)(2x+1)=10
c)-4(x-1)^2+(2x-1)(2x+1)=-3
giúp nhanh dùm mình nha
giải dùm em mấy câu này vs ạ nãy em ghi còn thiếu
em cảm ơn mn nhiều giải thích rọ dùm em luôn vs ạ


3.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;+\infty\right)\)
B đúng
4.
Từ BBT ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(0;1\right)\)
A đúng
1.
B sai (thiếu điều kiện \(f'\left(x\right)=0\) tại hữu hạn điểm)
Đúng 3
Bình luận (1)
Câu 2 đề thiếu yêu cầu
Câu 9:
Từ đồ thị ta thấy hàm đồng biến trên các khoảng \(\left(-\infty;0\right)\) và \(\left(2;+\infty\right)\)
\(\Rightarrow\) A đúng do \(\left(-1;0\right)\subset\left(-\infty;0\right)\)
Đúng 2
Bình luận (0)
\(x^4-4x=1\)
Giải pt bậc 4 này dùm mình vs!!!
Ta có : \(x^4-4x=1\Leftrightarrow x^4=4x+1\Leftrightarrow x^4+2x^2+1=2x^2+4x+2\)
\(\Leftrightarrow\left(x^2+1\right)^2=2\left(x+1\right)^2\Leftrightarrow\left(x^2+1\right)^2-2\left(x+1\right)^2=0\)
\(\Leftrightarrow\left[x^2+1-\sqrt{2}\left(x+1\right)\right].\left[x^2+1+\sqrt{2}\left(x+1\right)\right]=0\)
Đến đây thì dễ rồi ^^
Đúng 0
Bình luận (0)
Cho phương trình :\(k^2x^2+5kx+6=0\) trong đó k là một số đã cho:
a,Hãy tìm giá trị của k sao cho một trong các nghiệm của pương trình là x=1.
b, Hãy giải phương trình với giá trị của k vừa tìm được ở trên.
Giải phương trình:
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
Vì là câu 0,5 điểm nên là hơi khó,nên mn ai giải đc thì giải dùm mình với nhé
ĐKXĐ: \(\left\{{}\begin{matrix}2x+5>=0\\4-2x>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x>=-5\\2x< =4\end{matrix}\right.\Leftrightarrow-\dfrac{5}{2}< =x< =2\)
\(x^2+\sqrt{2x+5}+\sqrt{4-2x}=4x-1\)
=>\(x^2-4+\sqrt{2x+5}-3+\sqrt{4-2x}=4x-1-7\)
=>\(\left(x-2\right)\left(x+2\right)+\dfrac{2x+5-9}{\sqrt{2x+5}+3}+\sqrt{4-2x}=4x-8\)
=>\(\left(x-2\right)\left[\left(x+2\right)+\dfrac{2}{\sqrt{2x+5}+3}-4\right]+\sqrt{4-2x}=0\)
=>\(-\left(2-x\right)\left[\left(x-2\right)+\dfrac{2}{\sqrt{2x+5}+3}\right]+\sqrt{2\left(2-x\right)}=0\)
=>\(\sqrt{2-x}\left[-\sqrt{2-x}\left(x-2+\dfrac{2}{\sqrt{2x+5}+3}\right)+\sqrt{2}\right]=0\)
=>\(\sqrt{2-x}=0\)
=>x=2(nhận)
Đúng 4
Bình luận (0)
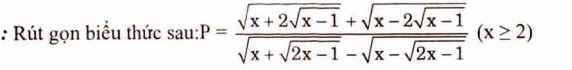 giải dùm e bài này vs ạ
giải dùm e bài này vs ạ
Lời giải:
\(P.\frac{1}{\sqrt{2}}=\frac{\sqrt{(x-1)+2\sqrt{x-1}+1}+\sqrt{(x-1)-2\sqrt{x-1}+1}}{\sqrt{(2x-1)+2\sqrt{2x-1}+1}-\sqrt{(2x-1)-2\sqrt{2x-1}+1}}\)
\(=\frac{\sqrt{(\sqrt{x-1}+1)^2}+\sqrt{(\sqrt{x-1}-1)^2}}{\sqrt{(\sqrt{2x-1}+1)^2}-\sqrt{(\sqrt{2x-1}-1)^2}}\)
\(=\frac{\sqrt{x-1}+1+\sqrt{x-1}-1}{\sqrt{2x-1}+1-(\sqrt{2x-1}-1)}=\frac{2\sqrt{x-1}}{2}=\sqrt{x-1}\)
Đúng 1
Bình luận (0)
giai phương trình sau
|2x+5|=|1-3x|
giải dùm mình nhé
Lập bảng xét dấu :
| x | \(\frac{-5}{2}\) | \(\frac{1}{3}\) | |||
| 2x+5 | - | 0 | + | \(|\) | + |
| 1-3x | + | \(|\) | + | 0 | - |
+) Nếu \(x\le\frac{-5}{3}\) thì \(|2x+5|=-2x-5\)
\(|1-3x|=1-3x\)
\(pt\Leftrightarrow-2x-5=1-3x\)
\(\Leftrightarrow-2x+3x=1+5\)
\(\Leftrightarrow x=6\)( loại )
+) Nếu \(\frac{-5}{2}< x< \frac{1}{3}\) thì \(|2x+5|=2x+5\)
\(|1-3x|=1-3x\)
\(pt\Leftrightarrow2x+5=1-3x\)
\(\Leftrightarrow2x+3x=1-5\)
\(\Leftrightarrow5x=-4\)
\(\Leftrightarrow x=\frac{-4}{5}\left(tm\right)\)
+) Nếu \(x\ge\frac{1}{3}\) thì \(|2x+5|=2x+5\)
\(|1-3x|=3x-1\)
\(pt\Leftrightarrow2x+5=3x-1\)
\(\Leftrightarrow2x-3x=-1-5\)
\(\Leftrightarrow-x=-6\)
\(\Leftrightarrow x=6\left(tm\right)\)
Vậy ....
Đúng 0
Bình luận (0)


















