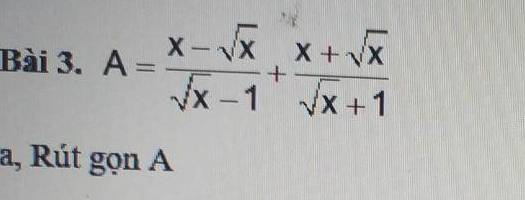
ai giải giúp mình câu này với ạ. mình cảm ơn
Ai giải thích giúp mình câu này với ạ, mình cảm ơn
TH1: thể 3 ở A, B, E
A-B-ddE- = 3.3.2.1.2 = 36
TH2: Thể 3 ở d
A-B-ddE- = 2.2.1.2 = 8
Tổng là 44
ai giúp mình câu này với ạ. mình cảm ơn
Ai làm giúp mình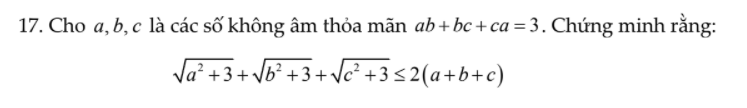 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn.
\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)
Ai giúp mình bài này với ạ!!! Giải chi tiết hộ mình nhé! Mình cảm ơn ạ!!!
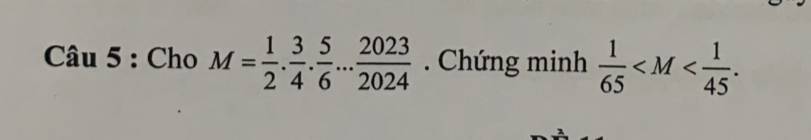
Ai giúp mình giải tự luận bài này với ạ!! Mình cảm ơn nhiều ạ!
`sin3x sinx+sin(x-π/3) cos (x-π/6)=0`
`<=> 1/2 (cos2x - cos4x) + 1/2(-sin π/6 + sin (2x-π/2)=0`
`<=> cos2x-cos4x-1/2+ sin(2x-π/2)=0`
`<=>cos2x-cos4x-1/2+ sin2x .cos π/2 - cos2x. sinπ/2=0`
`<=> cos2x - cos4x - cos2x = 1/2`
`<=> cos4x = cos(2π)/3`
`<=>` \(\left[{}\begin{matrix}4x=\dfrac{2\text{π}}{3}+k2\text{π}\\4x=\dfrac{-2\text{π}}{3}+k2\text{π}\end{matrix}\right.\)
`<=>` \(\left[{}\begin{matrix}x=\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\\x=-\dfrac{\text{π}}{6}+k\dfrac{\text{π}}{2}\end{matrix}\right.\)
\(sin3x.sinx+sin\left(x-\dfrac{\pi}{3}\right)cos\left(x-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x+\dfrac{1}{2}sin\left(2x-\dfrac{\pi}{2}\right)+\dfrac{1}{2}sin\left(-\dfrac{\pi}{6}\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}cos2x-\dfrac{1}{2}cos4x-\dfrac{1}{2}cos2x-\dfrac{1}{4}=0\)
\(\Leftrightarrow cos4x+\dfrac{1}{2}=0\)
\(\Leftrightarrow2cos^22x-1+\dfrac{1}{2}=0\)
\(\Leftrightarrow cos^22x=\dfrac{1}{4}\)
\(\Rightarrow cos2x=\pm\dfrac{1}{2}\)
Ai làm giúp mình 2 câu này với ạ! Mình cảm ơn.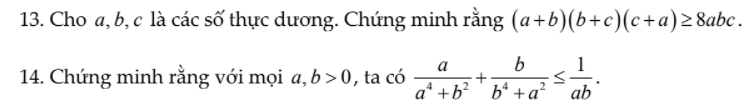
1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)
ai giúp mình giải bài này với ạ mình cảm ơn <33
bạn tự vẽ hình giúp mik nha
a. xét \(\Delta ADN\) và \(\Delta BAM\) có
AB=AD(gt)
\(\widehat{ADN}=\widehat{BAM}=90^o\)
DN=MA(N,M là trung điểm của cạnh DC,AD)
\(\Rightarrow\Delta ADN\sim\Delta BAM\left(c.g.c\right)\)
\(\Rightarrow\widehat{DNA}=\widehat{AMB}\)
mà:\(\widehat{DNA}+\widehat{DAN}=90^o\Rightarrow\widehat{BMA}+\widehat{DAN}=90^o\)
\(\Rightarrow\Delta MAI\) vuông tại I
\(\Rightarrow AI\perp MI\) hay \(MB\perp AN\)
b.ta có M là trung điểm của AD\(\Rightarrow AM=\dfrac{1}{2}AD=\sqrt{5}\)
trong \(\Delta MAB\) vuông tại A có
\(MB=\sqrt{AM^2+AB^2}=\sqrt{\sqrt{5^2}+\left(2\sqrt{5}\right)^2}=5\)
\(AM^2=MB.MI\Rightarrow MI=\dfrac{AM^2}{MB}=\dfrac{\sqrt{5^2}}{5^5}=0,2\)
\(AI.MB=AM.AB\Rightarrow AI=\dfrac{AM.AB}{MB}=\dfrac{\sqrt{5}.2\sqrt{5}}{5}\)=2
c.IB=MB-MI=5-0,2=4,8
\(S_{\Delta AIB}=\dfrac{AI.IB}{2}=\)\(\dfrac{2.4,8}{2}=4,8\)
\(S_{\Delta ADN}=\dfrac{AD.DN}{2}=\dfrac{2\sqrt{5}.\sqrt{5}}{2}=5\)
\(S_{\Delta ABCD}=\left(2\sqrt{5}\right)^2=20\)
\(S_{BINC}=S_{ABCD}-S_{\Delta AIB}-S_{\Delta DAN}\)=20-4,8-5=10,2
Ai giúp mình làm 3 câu này với ạ mình đang cần gấp. Cảm ơn mn nhiều ạ.
mọi người ơi giúp mình câu này với ạ, lời giải chi tiết càng tốt ạ, mình khá rối với câu này -.- cảm ơn mọi người nhiều
\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên