
Những câu hỏi liên quan
Cho tam giác ABC cân tại A . Kẻ trung tuyến AM . Từ M kẻ ME vuông goc với AB, MF vuông góc với AC a, Chứng minh ME=MFb, Chứng minh EF song song với BCc, Trên cạnh BC lấy điểm N bất kì , từ N kẻ NI vuông góc với AB , NK vuông góc với AC . Chứng minh khi vị trí của N thay đổi trên cạnh BC thì NI+NK không đổi
Xem chi tiết
a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A . Kẻ trung tuyến AM . Từ M kẻ ME vuông goc với AB, MF vuông góc với AC a, Chứng minh ME=MFb, Chứng minh EF song song với BCc, Trên cạnh BC lấy điểm N bất kì , từ N kẻ NI vuông góc với AB , NK vuông góc với AC . Chứng minh khi vị trí của N thay đổi trên cạnh BC thì NI+NK không đổi
Xem chi tiết
a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Đúng 1
Bình luận (0)
Cho tam giác ABC cân tại A . Kẻ trung tuyến AM . Từ M kẻ ME vuông goc với AB, MF vuông góc với AC a, Chứng minh ME=MF b, Chứng minh EF song song với BC c, Trên cạnh BC lấy điểm N bất kì , từ N kẻ NI vuông góc với AB , NK vuông góc với AC . Chứng minh khi vị trí của N thay đổi trên cạnh BC thì NI+NK không đổi
Xem chi tiết
a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A . Kẻ trung tuyến AM . Từ M kẻ ME vuông goc với AB, MF vuông góc với AC a, Chứng minh ME=MF
b, Chứng minh EF song song với BC
c, Trên cạnh BC lấy điểm N bất kì , từ N kẻ NI vuông góc với AB , NK vuông góc với AC . Chứng minh khi vị trí của N thay đổi trên cạnh BC thì NI+NK không đổi
Xem chi tiết
a: Xét ΔAMB và ΔAMC co
AM chung
MB=MC
AB=AC
=>ΔAMB=ΔAMC
=>góc MAB=góc MAC
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
=>ΔAEM=ΔAFM
=>AE=AF và ME=MF
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
c: IN//EM
=>NI/ME=BN/BM
=>NI/MF=BN/CM
=>NI/BN=MF/CM
FM//NK
=>MF/NK=CM/CN
=>MF/CM=NK/CN
=>NK/CN=NI/BN=(NI+NK)/BC ko đổi
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, M là trung điểm của BC,a)chứng minh tam giác amb=tam giác amc b)Từ M kẻ các đường ME vuông góc với Ab(E ∈ AB); MF vuông góc với Ac (F ∈ AC). Chứng minh ea=fa c)chứng minh ef song song bc
a, Vì Tam giác `ABC` cân tại A `=> AB = AC ;`\(\widehat{B}=\widehat{C}\)
Xét Tam giác `AMB` và Tam giác `AMC` có:
`AM chung`
\(\widehat{B}=\widehat{C}\) `(CMT)`
`MB = MC (g``t)`
`=>` Tam giác `AMB =` Tam giác `AMC (c-g-c)`
b, Vì Tam giác `AMB =` Tam giác `AMC (a)`
`=>` \(\widehat{EAM}=\widehat{FAM}\) (2 góc tương ứng).
Xét Tam giác `EAM` và Tam giác `FAM` có:
AM chung
\(\widehat{EAM}=\widehat{FAM}\) `(CMT)`
\(\widehat{AEM}=\widehat{AFM}=90^0\)
`=>` Tam giác `EAM =` Tam giác `FAM (ch-gn)`
`=> EA = FA` (2 cạnh tương ứng).
c, *câu này mình hơi bí bn ạ:')
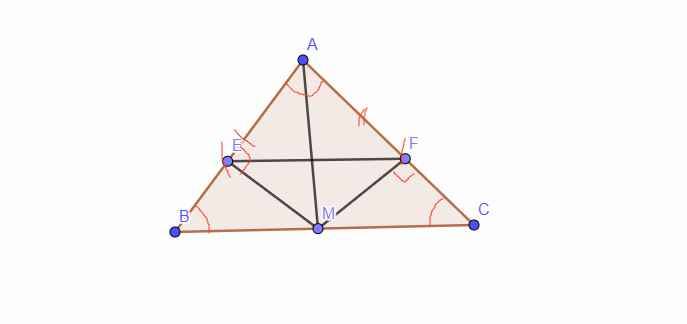
Đúng 2
Bình luận (0)
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b: Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
góc EAM=góc FAM
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F a) Chứng minh: ∆BEM ∆CFM b) Chứng minh AM là trung trực của đoạn thẳng EF c) Chứng minh EF//BC d) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
Đọc tiếp
Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc với AC tại F a) Chứng minh: ∆BEM = ∆CFM b) Chứng minh AM là trung trực của đoạn thẳng EF c) Chứng minh EF//BC d) Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C, hai đường thẳng này cắt nhau ở D. Chứng minh ba điểm A, M, D thẳng hàng
a: Xét ΔEBM vuông tại E và ΔFCM vuông tại F có
MB=MC
góc B=góc C
=>ΔEBM=ΔFCM
b: Xet ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
ME=MF
=>ΔAEM=ΔAFM
=>AE=AF
mà ME=MF
nên AM là trung trực của EF
c: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
d: Xet ΔABD vuông tại B và ΔACD vuông tại C có
AD chung
AB=AC
=>ΔABD=ΔACD
=>BD=CD
=>D nằm trên trung trực của BC
=>A,M,D thẳng hàng
Đúng 2
Bình luận (0)
Cho tam giác ABC có AB = AC. M là trung điểm của BC. a) chứng minh tam giác AMB bằng tam giác AMC. b) từ M kẻ ME vuông góc với AB và MF vuông góc với AC. Chứng minh rằng AE = EF c) chứng minh EF song song với BC b) từ B kẻ đường thẳng vuông góc với AB. Từ C kẻ đường thẳng vuông góc với AC. Hai đường thẳng này cắt nhau tại N. Chứng minh rằng A,M,N thẳng hàng.
a: Xét ΔAMB và ΔAMC có
AM chung
MB=MC
AB=AC
Do đó: ΔAMB=ΔAMC
b:Sửa đề: Chứng minh AE=AF
Ta có: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
Ta có: ΔABM=ΔACM
=>\(\widehat{BAM}=\widehat{CAM}\)
Xét ΔAEM vuông tại E và ΔAFM vuông tại F có
AM chung
\(\widehat{EAM}=\widehat{FAM}\)
Do đó: ΔAEM=ΔAFM
=>AE=AF
c: Xét ΔABC có \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
nên EF//BC
d: Xét ΔABN vuông tại B và ΔACN vuông tại C có
AN chung
AB=AC
Do đó: ΔABN=ΔACN
=>BN=CN
=>N nằm trên đường trung trực của BC(1)
Ta có; ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường trung trực của BC(2)
Từ (1) và (2) suy ra A,M,N thẳng hàng
Đúng 1
Bình luận (1)
Câu 10: Cho tam giác ABC cân tại A, vẽ trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, kẻ MF vuông góc Với AC tại F.
a) Chứng minh ![]()
b) Chứng minh AM là trung trực của EF.
b) ta có tam giác ABC cân
=> \(\widehat{B}=\widehat{C}=180-\widehat{A}\) (1)
mà AM là trung tuyến => AM cx là phân giác và AM cx là đường cao (t/c tam giác cân)
=>\(\widehat{A1}=\widehat{A2}\)
xét tam giác AEM và tam giác AfM
có AM chung
\(\widehat{E}=\widehat{F}\)=90o
\(\widehat{A1}=\widehat{A2}\)
=> tam giác AEM =tam giác AFM (CH-GN)
=> AE =AC (2 cạnh tương ứng)
=> tam giác AEF cân ở \(\widehat{A}\)
=> \(\widehat{E}=\widehat{F}=180-\widehat{A}\) (2)
từ 1 và 2 =>\(\widehat{E}=\widehat{B}\) mà 2 góc ở vt đồng vị
=> EF // BC
mà AM ⊥ BC
=> EF ⊥ AM
=> AM là trung trực của EF (t/c tam giác cân)
Đúng 0
Bình luận (1)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC(M là trung điểm của BC)
\(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng) và EB=FC(Hai cạnh tương ứng)
Ta có: AE+EB=AB(E nằm giữa A và B)
AF+FC=AC(F nằm giữa A và C)
mà EB=FC(cmt)
và AB=AC(ΔBAC cân tại A)
nên AE=AF
Ta có: AE=AF(cmt)
nên A nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: ME=MF(cmt)
nên M nằm trên đường trung trực của EF(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM là đường trung trực của EF(Đpcm)
Đúng 0
Bình luận (0)
Cho tam giác cân ABC (AB = AC). Trung tuyến AM. Từ M kẻ ME vuông góc với AB tại E, MF vuông góc với AC tại F
a, Chứng minh ME = MF
b, Chứng minh AM là trung trực của EF
c, Từ B kẻ đường thẳng vuông góc với AB tại B, từ C kẻ đường thẳng vuông góc với AC tại C. 2 đường thẳng này cắt nhau tại D. Chứng minh 3 điểm A,M,D thẳng hàng
Xét tam giác ABM và tam giác ACM
có : + AB = AC (gt)
+ BM = CM (gt)
+) AM chung
=> tam giác ABM = tam giác ACM (c.c.c)
=> góc A1 = góc A2
Xét tam giác AEM và tam giác AFM có :
+) góc AME = góc AMF (Vì góc MEA = MFA (= 90o) ; góc A1 = góc A2 => góc MEA - góc A1 = góc MFA - góc A2 => <AME = <AMF)
+ góc A1 = góc A2
+) AM chung
=> Tam giác AEM = Tam giác AFM (g.c.g)
=> ME = MF (cạnh tương ứng)
=> AE = AF
b) Gọi K là giao điểm của AM và EF
Xét tam giác AEK và tam giác AFK có
+) góc A1 = góc A2
+) AF = AE (cmt)
+) AK chung
=> tam giác AEK = tam giác AFK (c.g.c)
=> EK = FK (cạnh tương ứng)
=> góc AKE = góc AKF (góc tương ứng)
Lại có góc AKE + góc AKF = 180 o
=> góc AKE = góc AKF = 90o
mà EK = FK
=> AK là trung trực của EF
mà K \(\in\)AM
=> AM là trung trực của EF
c) Vì tam giác ABM = tam giác ACM (cmt)
=> góc AMB = góc AMC
Mà góc AMB + góc AMC = 180 o
=> góc AMB = góc AMC = 90o
lạ có MC = MB = 1/2BC
=> AM là trung trực của BC (1)
Vì góc AMB = góc AMC = 90o
mà góc AMB + góc BMD = góc AMC + góc CMD (=180o)
=> góc BMD = góc CMD = 90o
lại có BM = CM = 1/2BC
=> MD là trung trực của BC (2)
Từ (1) (2) => A;M;D thẳng hàng
















