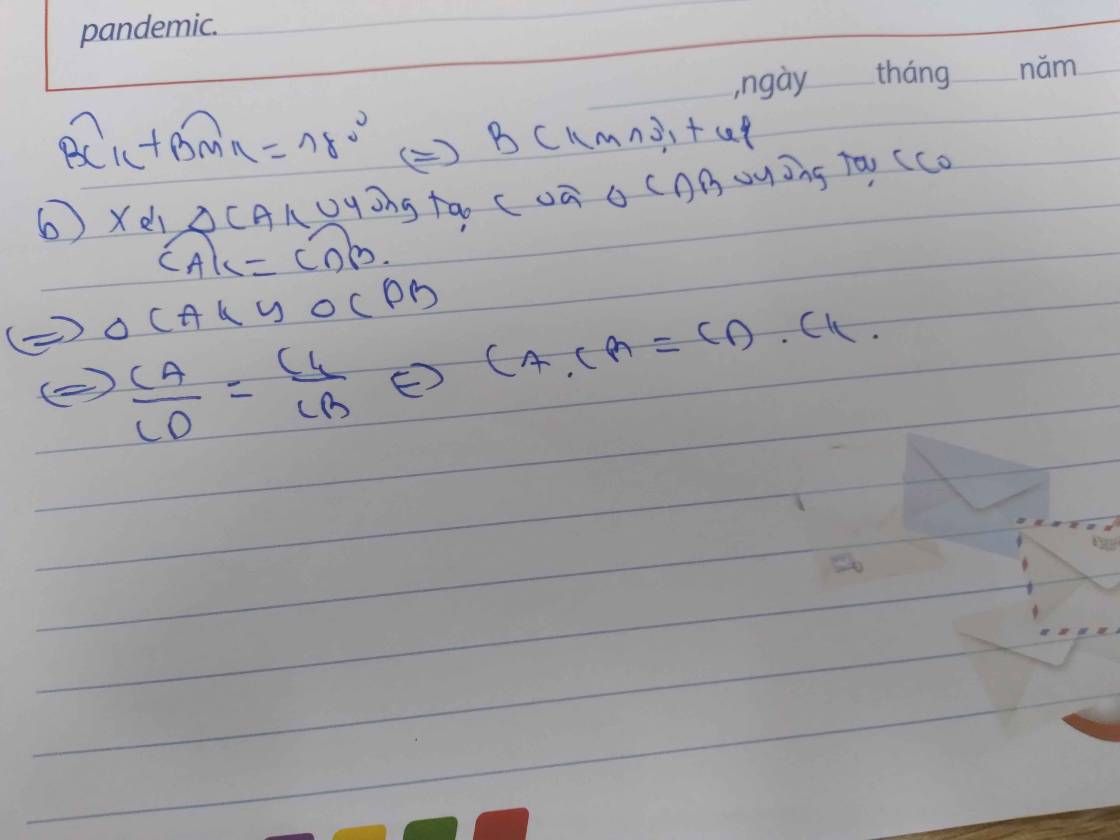Những câu hỏi liên quan
Làm mik 2 câu cuối thôi nhé, 2câu đầu t làm rồi Cho nửa đường tròn tâm O đường kính AB2R (kí hiệu là (O)). Qua trung điểm I của OA, vẽ tia Ix vuông góc với AB và cắt (O) tại K. Gọi M là điểm di động trên đoạn IK ( M khác I và K), kéo dài AM cắt (O) tại C. Tia Ix cắt đường thẳng BC tại D và cắt tiếp tuyến tại C của (O) tại E.1) Chứng minh tứ giác IBCM nội tiếp.2) Chứng minh tam giác CEM cân tại E.3) Khi M là trung điểm của IK, tính diện tích tam giác ABD theo R.4) Chứng tỏ rằng tâm đường tròn ngo...
Đọc tiếp
Làm mik 2 câu cuối thôi nhé, 2câu đầu t làm rồi
Cho nửa đường tròn tâm O đường kính AB=2R (kí hiệu là (O)). Qua trung điểm I của OA, vẽ tia Ix vuông góc với AB và cắt (O) tại K. Gọi M là điểm di động trên đoạn IK ( M khác I và K), kéo dài AM cắt (O) tại C. Tia Ix cắt đường thẳng BC tại D và cắt tiếp tuyến tại C của (O) tại E.
1) Chứng minh tứ giác IBCM nội tiếp.
2) Chứng minh tam giác CEM cân tại E.
3) Khi M là trung điểm của IK, tính diện tích tam giác ABD theo R.
4) Chứng tỏ rằng tâm đường tròn ngoại tiếp tam giác AMD thuộc một đường thẳng cố định khi M thay đổi.
cho đường tròn tâm O , đường kính AB . gọi C là trung điểm của OA, kẻ tia Cx vuông góc với AB va cắt nửa đường tròn tâm O tại I . K là điểm bất kỳ trên cạnh CI (K khác C , K khác I) . tia AK cắt nửa đường tròn tâm O tại M , tia BM cắt Cx tại D . tiếp tuyến tại M của nửa đường tròn tâm O cắt Cx tại NA/ chứng minh tứ giác ACMD nội tiếp đường trònB/chứnng minh tam giác MNK cânc/ gọi E là điểm đối xứng với B qua C , chứng minh tứ giác AKDE nội tiếpthankkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
Đọc tiếp
cho đường tròn tâm O , đường kính AB . gọi C là trung điểm của OA, kẻ tia Cx vuông góc với AB va cắt nửa đường tròn tâm O tại I . K là điểm bất kỳ trên cạnh CI (K khác C , K khác I) . tia AK cắt nửa đường tròn tâm O tại M , tia BM cắt Cx tại D . tiếp tuyến tại M của nửa đường tròn tâm O cắt Cx tại N
A/ chứng minh tứ giác ACMD nội tiếp đường tròn
B/chứnng minh tam giác MNK cân
c/ gọi E là điểm đối xứng với B qua C , chứng minh tứ giác AKDE nội tiếp
thankkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkkk
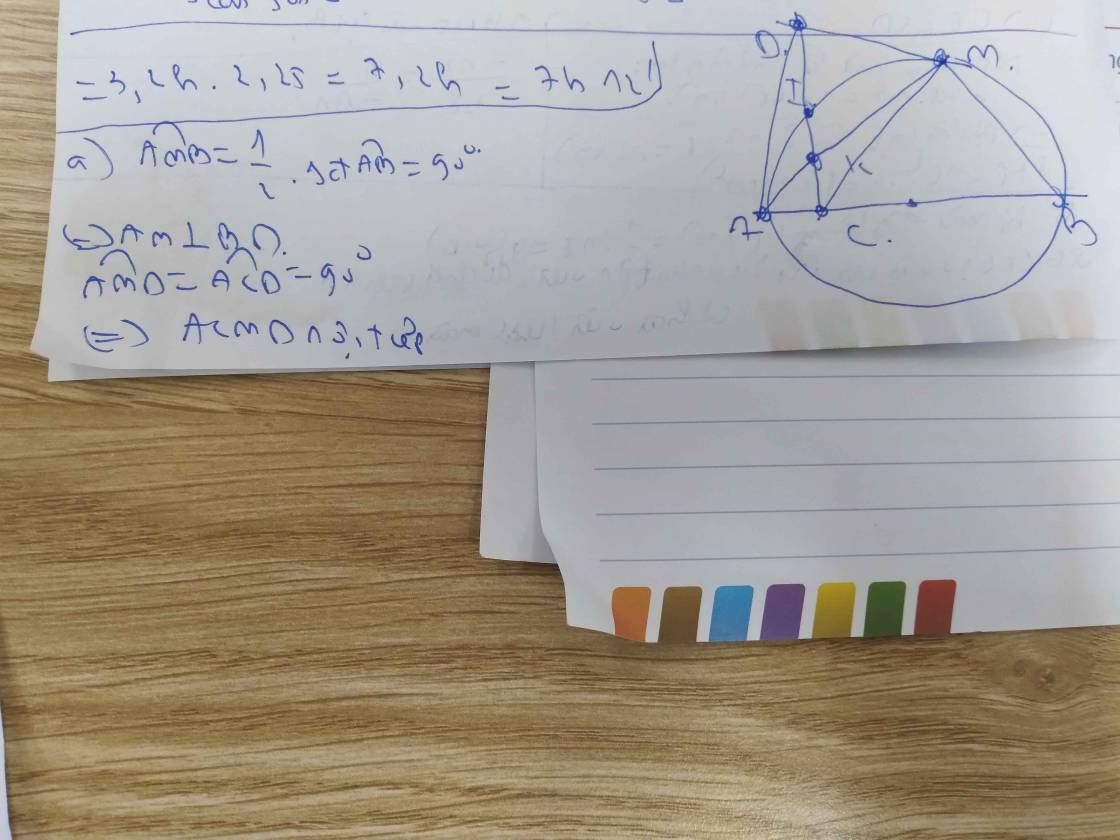
a) Vì AB là đường kính \(\Rightarrow\angle AMB=90\Rightarrow\angle ACD=\angle AMD=90\)
\(\Rightarrow ACMD\) nội tiếp
b) Ta có: \(\angle KCB+\angle KMB=90+90=180\Rightarrow KCBM\) nội tiếp
\(\Rightarrow\angle AKC=\angle MBA\)
Ta có: \(\angle NMK=\angle MBA=\angle AKC=\angle MKN\)
\(\Rightarrow\Delta NMK\) cân tại N
c) Vì B và E đối xứng với nhau qua C \(\Rightarrow\) CD là trung trực BE
\(\Rightarrow\angle DEC=\angle DBC=\angle AKC\Rightarrow AKDE\) nội tiếp
Đúng 2
Bình luận (1)
Cho nửa đường tròn tâm (O) đường kính AB 2R. I là trung điểm của OA, IK vuông góc với AB cắt nửa đường tròn tại K. Điểm C bất kỳ thuộc đoạn IK, AC cắt nửa đường tròn tại M. Tiếp tuyến tại M cắt IK tại N; IK cắt BM tại D. Chứng minh tam giác CMN cân Tính CD theo R trường hợp C là trung điểm của IK. c) Gọi E là điểm đốia xứng của B qua I. Chứng minh khi C chuyển động trên IK thì tâm đường tròn ngoại tiếp ACD di động trên một đường cố định.
Đọc tiếp
Cho nửa đường tròn tâm (O) đường kính AB = 2R. I là trung điểm của OA, IK vuông góc với AB cắt nửa đường tròn tại K. Điểm C bất kỳ thuộc đoạn IK, AC cắt nửa đường tròn tại M. Tiếp tuyến tại M cắt IK tại N; IK cắt BM tại D. Chứng minh tam giác CMN cân Tính CD theo R trường hợp C là trung điểm của IK. c) Gọi E là điểm đốia xứng của B qua I. Chứng minh khi C chuyển động trên IK thì tâm đường tròn ngoại tiếp ACD di động trên một đường cố định.
Cho đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm của OA; qua C kẻ đường thẳng vuông góc với OA cắt đường tròn đó tại hai điểm phân biệt M và N. Trên cung nhỏ BM lấy điểm K ( K khác B và M), trên tia KN lấy điểm I sao cho KI = KM. Gọi H là giao điểm của AK và MN. Chứng minh rằng:
1. Tứ giác BCHK là tứ giác nội tiếp.
2. AK.AH = R2
Cho nửa đường tròn tâm O đường kính AB = 2R. C là trung điểm của đoạn OA, đường thẳng Cx vuông góc với AB, Cx cắt nửa đường tròn ( O ) tại I. K là 1 điểm bất kì nằm trên đoạn CI ( K khác C, K khác I ), tia AK cắt nửa đường tròn tại M.
Tính diện tích tam giác ABD khi K là trung điểm của đoạn thẳng CI?
Ơ , em tưởng chị " ko cần bít " cơ mà ?
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB và M là một điểm tùy ý trên nửa đường tròn (M khác A, B). Lấy điểm I thuộc đoạn thẳng MB (I khác B, M). Kẻ IH vuông góc với AB (H thuộc AB). Tia AI cắt nửa đường tròn tại N. Tia AM cắt tia BN tại Cb)Gọi K là giao điểm của tia BN và tiếp tuyến tại A của nửa đường tròn (O). Khi tứ giác AICK nội tiếp được đường tròn, chứng minh MH vuông góc với MN. c) Chứng minh rằng: IH/ IC+ IA/ IN+ IB/ IM 6
Đọc tiếp
Cho nửa đường tròn tâm O, đường kính AB và M là một điểm tùy ý trên nửa đường tròn (M khác A, B). Lấy điểm I thuộc đoạn thẳng MB (I khác B, M). Kẻ IH vuông góc với AB (H thuộc AB). Tia AI cắt nửa đường tròn tại N. Tia AM cắt tia BN tại C
b)Gọi K là giao điểm của tia BN và tiếp tuyến tại A của nửa đường tròn (O). Khi tứ giác AICK nội tiếp được đường tròn, chứng minh MH vuông góc với MN.
c) Chứng minh rằng: IH/ IC+ IA/ IN+ IB/ IM >6
b) Dễ thấy C là trực tâm của tam giác IAB nên C, I, H thẳng hàng.
Do tứ giác AICK là hình thang nội tiếp được đường tròn nên là hình thang cân.
Khi đó \(\widehat{IAK}=\widehat{CKA}\Rightarrow\widehat{IAB}=\widehat{NBA}\)
Suy ra tam giác NAB vuông cân tại N nên \(\widehat{NBA}=45^o\).
Ta có các tứ giác CMIN, AMIH nội tiếp được nên \(\widehat{NMH}=\widehat{NMI}+\widehat{HMI}=\widehat{ICN}+\widehat{IAB}=45^o+45^o=90^o\Rightarrow MN\perp MH\).
Đúng 2
Bình luận (0)

c) Đề phải là \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}\ge6\).
Đặt \(x=\dfrac{IH}{CH};y=\dfrac{IN}{AN};z=\dfrac{IM}{BM}\left(x,y,z< 1\right)\).
Ta có \(x+y+z=\dfrac{S_{IAB}}{S_{ABC}}+\dfrac{S_{IBC}}{S_{ABC}}+\dfrac{S_{ICA}}{S_{ABC}}=1\).
Lại có \(\dfrac{IH}{CH}=x\Rightarrow\dfrac{CH}{IH}=\dfrac{1}{x}\Rightarrow\dfrac{IC}{IH}=\dfrac{1}{x}-1\).
Tương tự \(\dfrac{IA}{IN}=\dfrac{1}{y}-1;\dfrac{IB}{IM}=\dfrac{1}{z}-1\).
Do đó \(\dfrac{IC}{IH}+\dfrac{IA}{IN}+\dfrac{IB}{IM}=\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}-3\ge_{Svacxo}\dfrac{9}{x+y+z}-3=\dfrac{9}{1}-3=6\).
Vậy ta có đpcm.
Đúng 0
Bình luận (0)
1) Cho nửa đường tròn tâm O đường kính AB 2R. Gọi C là trung điểm OA, tia Cx vuôn góc AB, Cx cắt nửa đường tròn (O) tại I. Lấy K là 1 điểm bất kì trên CI (K khác C và I). AK cắt nửa đường tròn (O) tại M. Tiếp tuyến với (O) tại M cắt Cx tại N. BM cắt Cx tại D. a) CM: 4 điểm A, C, M, D thuộc 1 đường tròn b) CM: tam giác MNK cân c) Tính diện tích ABD khi K là trung điểm CI d) Chứng minh K di động trên đoạn CI thì tâm đường tròn ngoại tiếp tam giác AKD nằm trên 1 đường thẳng cố định. Cảm ơn trước n...
Đọc tiếp
1) Cho nửa đường tròn tâm O đường kính AB = 2R. Gọi C là trung điểm OA, tia Cx vuôn góc AB, Cx cắt nửa đường tròn (O) tại I. Lấy K là 1 điểm bất kì trên CI (K khác C và I). AK cắt nửa đường tròn (O) tại M. Tiếp tuyến với (O) tại M cắt Cx tại N. BM cắt Cx tại D.
a) CM: 4 điểm A, C, M, D thuộc 1 đường tròn
b) CM: tam giác MNK cân
c) Tính diện tích ABD khi K là trung điểm CI
d) Chứng minh K di động trên đoạn CI thì tâm đường tròn ngoại tiếp tam giác AKD nằm trên 1 đường thẳng cố định.
Cảm ơn trước nhé
bn làm đk đến câu c chưa z?
mình mới chỉ làm được a và b thui
Đúng 0
Bình luận (0)
Xét △AKC và △DBC có: C = 900, góc KAC = góc CDB (cùng phụ với góc B) => △AKC đồng dạng với △DBC => AC/DC = KC/BC=> KC.DC = AC.BC (✳)
Cũng có △IAB vuông tại I có IC vuông góc với AB nên theo hệ thức lượng trong tam giác vuông ta có IC2=AC.CB (**)
Từ (*) và (**) => KC.DC=IC2 => KC/IC=IC/DC=1/2 => DC = 2IC
IC2=AC.BC=1/2R . 3/2R = 3/4R2 =>IC = \(\sqrt{ }\)3/2 R=> DC = căn 3 R.
S△ADB = 1/2 DC.AB=căn 3 R2
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh: 1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn. 2) CK.CD CA.CB 3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kỳ nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt tia CI tại D. Chứng minh:
1) Các tứ giác: ACMD; BCKM nội tiếp đường tròn.
2) CK.CD = CA.CB
3) Gọi N là giao điểm của AD và đường tròn (O) chứng minh B, K, N thẳng hàng
1:
góc AMB=1/2*sđ cung AB=90 độ
=>AM vuông góc BD
góc ACD=góc AMD=90 độ
=>ACMD nội tiếp
góc KCB+góc KMB=180 độ
=>BMKC nội tiếp
2: Xét ΔCAK vuông tại C và ΔCDB vuông tại C có
góc CAK=góc CDB
=>ΔCAK đồng dạng với ΔCDB
=>CA/CD=CK/CB
=>CA*CB=CD*CK
Đúng 1
Bình luận (0)
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :a) Các tứ giác : ACMD ; BCKM nội tiếp đường trònb) CK.CD CA.CBc) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. C là một điểm nằm giữa O và A. Đường thẳng vuông góc với AB tại C cắt nửa đường tròn trên tại I. K là một điểm bất kì nằm trên đoạn thẳng CI (K khác C và I), tia AK cắt nửa đường tròn (O) tại M, tia BM cắt CI tại D. Chứng minh :
a) Các tứ giác : ACMD ; BCKM nội tiếp đường tròn
b) CK.CD = CA.CB
c) Gọi N là giao điểm của AD và (O). Chứng minh rằng : B, K, M thẳng hàng