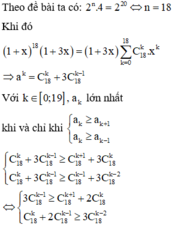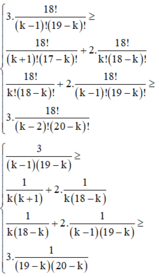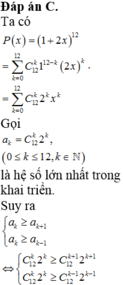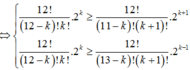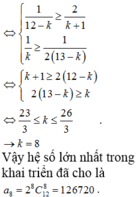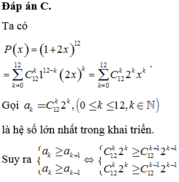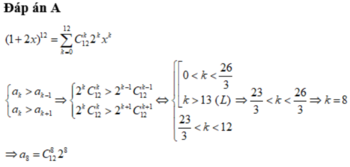Tìm hệ số lớn nhất trong khai triển của (a+b)6

Những câu hỏi liên quan
Cho khai triển
1
+
x
n
1
+
3
x
a
0
+
a
1
x
+
a
2
x
+
.
.
.
+
a
n
+...
Đọc tiếp
Cho khai triển 1 + x n 1 + 3 x = a 0 + a 1 x + a 2 x + . . . + a n + 1 x n + 1 . Tìm hệ số lớn nhất trong khai triển trên biết rằng tổng các hệ số của khai triển đó bằng 2 20 .
A. 277134
B. 189618
C. 48620
D. 179894
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của P x = 1 + 2 x 12
A. 126700
B. 126730
C. 126720
D. 126710
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của P x = 1 + 2 x 12
A. 126700.
B. 126730.
C. 126720.
D. 126710.
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của P ( x ) = 1 + 2 x 12
A. 126700.
B. 126730.
C. 126720.
D. 126710.
Đáp án C
Ta có P ( x ) = 1 + 2 x 12 = ∑ k = 0 12 C 12 k 1 12 - k = ∑ k = 0 12 C 12 k 2 k x k .
Gọi a k = C 12 K 2 K , 0 ≤ k ≤ 12 , k ∈ ℕ là hệ số lớn nhất trong khai triển.
Suy ra a k ≥ a k + 1 a k ≥ a k - 1 ⇔ c 12 k 2 k ≥ c 12 k + 1 2 k + 1 c 12 k 2 k ≥ c 12 k - 1 2 k - 1
⇔ 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 11 - k ! k + 1 ! . 2 k + 1 12 ! 12 - k ! k ! . 2 k ≥ 12 ! 13 - k ! k + 1 ! . 2 k - 1 ⇔ 1 12 - k ≥ 2 k + 1 1 k ≥ 1 2 13 - k
Vậy hệ số lớn nhất trong khai triển đã cho là a 8 = 2 8 c 12 8 = 126720 .
Đúng 0
Bình luận (0)
Cho khai triển
P
x
1
+
2
x
12
a
0
+
a
1...
Đọc tiếp
Cho khai triển P x = 1 + 2 x 12 = a 0 + a 1 x + ... + a 12 x 12 . Tìm hệ số a k 0 ≤ k ≤ 12 lớn nhất trong khai triển trên.
A. C 12 8 2 8 .
B. C 12 9 2 9 .
C. C 12 10 2 10 .
D. 1 + C 12 8 2 8 .
Cho khai triển
P
x
1
+
2
x
12
a
0
+
a
1
x
+
.
.
.
+
a
12
x
12
. Tìm hệ số
a
k
(...
Đọc tiếp
Cho khai triển P x = 1 + 2 x 12 = a 0 + a 1 x + . . . + a 12 x 12 . Tìm hệ số a k ( 0 ≤ k ≤ 12 ) lớn nhất trong khai triển trên
A. C 12 8 2 8
B. C 12 9 2 9
C. C 12 10 2 10
D. 1 + C 12 8 2 8
Tìm hệ số lớn nhất trong các hệ số của các số hạng khi khai triển nhị thức sau thành đa thức (1+x)101
Giúp với ạ
Hệ số lớn nhất sẽ tương ứng với số hạng đứng chính giữa
=>Hệ số lớn nhất là \(C^{51}_{101}\)
Đúng 2
Bình luận (0)
Tìm hệ số lớn nhất trong khai triển nhị thức Newton của \(\left(\dfrac{1}{2}+\dfrac{x}{3}\right)^{14}\)
Bài 1: Tìm hệ số lớn nhất trong khai triển (x+2)\(^{10}\)
helppp me
SHTQ: \(C_{10}^k.2^k.x^{10-k}\) có hệ số: \(a_k=C_{10}^k2^k\)
Hệ số lớn nhất khi thỏa mãn:
\(\left\{{}\begin{matrix}a_k\ge a_{k+1}\\a_k\ge a_{k-1}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}C_{10}^k2^k\ge C_{10}^{k+1}2^{k+1}\\C_{10}^k2^k\ge C_{10}^{k-1}2^{k-1}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{10!}{k!\left(10-k\right)!}\ge\dfrac{10!}{\left(k+1\right)!\left(10-\left(k+1\right)\right)!}.2\\\dfrac{10!}{k!\left(10-k\right)!}.2\ge\dfrac{10!}{\left(k-1\right)!\left(10-\left(k-1\right)\right)!}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{10-k}\ge\dfrac{2}{k+1}\\\dfrac{2}{k}\ge\dfrac{1}{11-k}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}k\ge\dfrac{19}{3}\\k\le\dfrac{22}{3}\end{matrix}\right.\) \(\Rightarrow k=7\)
Hệ số lớn nhất: \(C_{10}^7.2^7\)
Đúng 1
Bình luận (0)