tìm x,y tm x^2+2x^2y^2+2y^2-(x^2+y^2+2x^2)-2=0

Những câu hỏi liên quan
tìm cặp x, y tm:
\(\hept{\begin{cases}\sqrt{2x^2y-x^4y^2}-y^2+x^2\left(x-1\right)=0\\\sqrt{1+\left(x+y\right)^2}+x\left(2y+x^2\right)\le0\end{cases}}\)
Tìm x,y∈N* sao cho
\(a,x^2y^2\left(y-x\right)=5y^2-27\\ b,x^4-x^2+2x^2y-2xy+2y^2-2y-36=0\)
Tìm x,y biết:
a,2x^2+y^2+2xy+10x+25=0
b,x^2+3y^2+2xy-2y+1=0
c,x^2+2y^2+2xy-2x+2=0
a) \(2x^2+y^2+2xy+10x+25=0\)
\(\Leftrightarrow x^2+x^2+y^2+2xy+10x+25=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(x^2+10x+25\right)=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(x+5\right)^2=0\)
Vì \(\hept{\begin{cases}\left(x+y\right)^2\ge0\forall x\\\left(x+5\right)^2\ge0\forall x\end{cases}}\)
\(\Rightarrow\left(x+y\right)^2+\left(x+5\right)^2\ge0\forall x\)
Vậy đẳng thức xảy ra\(\Leftrightarrow\hept{\begin{cases}x+y=0\\x+5=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=-5\\y=5\end{cases}}\)
Đúng 0
Bình luận (0)
b)\(x^2+3y^2+2xy-2y+1=0\)
\(\Leftrightarrow x^2+y^2+2y^2+2xy-2y+\frac{1}{2}+\frac{1}{2}=0\)
\(\Leftrightarrow\left(x^2+2xy+y^2\right)+\left(2y^2-2y+\frac{1}{2}\right)+\frac{1}{2}=0\)
\(\Leftrightarrow\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}=0\)
Vì \(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2\ge0\)
nên \(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}>0\)
Mà\(\left(x+y\right)^2+\left(\sqrt{2}y-\frac{1}{\sqrt{2}}\right)^2+\frac{1}{2}=0\)
nên pt vô nghiệm
Đúng 0
Bình luận (0)
a) 2x2 + y2 + 2xy + 10x + 25 = 0
=> (x2 + 2xy + y2) + (x2 + 10x + 25) = 0
=> (x + y)2 + (x + 5)2 = 0
<=> \(\hept{\begin{cases}x+y=0\\x+5=0\end{cases}}\) <=> \(\hept{\begin{cases}y=-x\\x=-5\end{cases}}\) <=> \(\hept{\begin{cases}y=5\\x=-5\end{cases}}\)
b)c) xem lại đề
Đúng 0
Bình luận (0)
1) \(\left\{{}\begin{matrix}xy+x+y=x^2-2y^2\\x\sqrt{2y}-y\sqrt{x-1}=2x-2y\end{matrix}\right.\)
2) \(\left\{{}\begin{matrix}2x^2+y^2-3xy+3x-2y+1=0\\4x^2-y^2+x+4=\sqrt{2x+y}+\sqrt{x+4y}\end{matrix}\right.\)
Giải hệ pt:
a)(x+√(x^2+4))(y+√(y^2+1))=2 và 27x^6=x^3-8y+2
b)(8x-3)√(2x-1) -y-4y^3=0 và 4x^2-8x+2y^3+y^2-2y+3=0
c) x(1+y-x)=-2y^2-y và x(√2y -2)=y(√(x-1)-2)
d) √(x+2y)+√(2x-y)+x^2y=√x+√3y+xy^2 và 2(1-y)√(x^2+2y-1)=y^2-2x-1
e)(y-2x+√y-√x)/√xy +1=0 và √(1-xy) +x^2-y^2=0
CÁC BẠN ƠI..GIÚP MK VS Ạ...MAI MK HOK R...CẢM ƠM TRƯỚC Ạ...☺️☺️☺️
phân tích đa thức sau thành nhân tử
1,3x^2+x-2
2, 2x^2-3xy-2y^2
3, 2x^2-3xy-2y^2
4, x^2+4xy+2x+3y^2+6
5, x^8+x+1
Tìm x,y biết
1, x^2+2x+5+y^2-4y=0
2,4x^2+y^4-20x-2y=26=0
mik ko bít
I don't now
................................
.............
Đúng 0
Bình luận (0)
x^2+2x^2y^2+2y^2-(x^2y^2+2x^2)-2=0 tim x va y
Bài 1 : Tính giá trị biểu thức sau , biết x+y-2=0
a ) M = x^3+x^2y+2x^2-xy-y^2+3y+x-1
b ) N= x^3-2x^2-xy^2+2xy+2y+2x-2
c ) P = x^4+2x^3y-2x^3+x^2y^2-2x^2y-x*(x+y )+2x+3
Biến đổi mỗi đa thức theo hướng làm xuất hiện thừa số x+y-2 \(M=x^3+x^2y-2x^2-xy-y^2+3y+x-1\)
\(M=x^3+x^2y-2x^2-xy-y^2+\left(2y+y\right)+x-\left(-2+1\right)\)
\(M=\left(x^3+x^2y-2x^2\right)-\left(xy+y^2-2y\right)+\left(x+y-2\right)+1\)
\(M=\left(x^2.x+x^2.y-2x^2\right)-\left(x.y+y.y-2y\right)+\left(x+y-2\right)+1\)
\(M=x^2.\left(x+y-2\right)-y.\left(x+y-2\right)+\left(x+y-2\right)+1\)
\(M=x^2.0+y.0+0+1\)
\(M=1\)
\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-2\)
\(N=x^3+x^2y-2x^2-xy^2+x^2y+2xy+2y+2x-\left(-4+2\right)\)
\(N=\left(x^3+x^2y-2x^2\right)-\left(x^2y+xy^2-2xy\right)+\left(2x+2y-4\right)+2\)
\(N=\left(x^2x+x^2y-2x^2\right)-\left(xyx+xyy-2xy\right)+\left(2x+2y-4\right)+2\)
\(N=x^2\left(x+y-2\right)-xy\left(x+y-2\right)+2\left(x+y-2\right)+2\)
\(N=x^2.0-xy.0+2.0+2\)
\(N=2\)
\(P=x^4+2x^3y-2x^3+x^2y^2-2x^2y-x\left(x+y\right)+2x+3\)
\(P=\left(x^4+x^3y-2x^3\right)+\left(x^3y+x^2y^2-2x^2y\right)-\left(x^2+xy-2x\right)+3\)\(P=\left(x^3x+x^3y-2x^3\right)+\left(x^2y.x+x^2yy-2x^2y\right)-\left(xx+xy-2x\right)+3\)
\(P=x^3\left(x+y-2\right)+x^2y\left(x+y-2\right)-x\left(x+y-2\right)+3\)
\(P=x^3.0+x^2y.0-x.0+3\)
\(P=3\)
Tích mình nha!![]()
![]()
Đúng 1
Bình luận (1)
bn nào viết rõ hơn giùm mik đc ko.
(a^2+b^2)(x^2+y^2)=(ax+by)^2
<=> a^2x^2 + a^2y^2 + b^2x^2 + b^2y^2 = a^2x^2 + 2abxy + b^2y^2
<=> a^2y^2 + b^2x^2 = 2abxy
<=> a^2y^2 + b^2x^2 - 2abxy = 0
<=> (ay - bx)^2 = 0
=> ay - bx = 0
=> ay = bx
=> a/x = b/y ( x,y khác 0)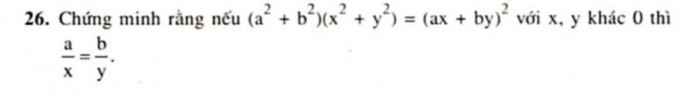
Ta có: \(\left(ax+by\right)^2=\left(a^2+b^2\right)\left(x^2+y^2\right)\)
\(\Leftrightarrow a^2x^2+2abxy+b^2y^2=a^2x^2+a^2y^2+x^2b^2+b^2y^2\)
\(\Leftrightarrow2abxy=a^2y^2+x^2b^2\)
\(\Leftrightarrow\left(ay-xb\right)^2=0\)
\(\Leftrightarrow ay=xb\)
hay \(\dfrac{a}{x}=\dfrac{b}{y}\)
Đúng 1
Bình luận (0)
















