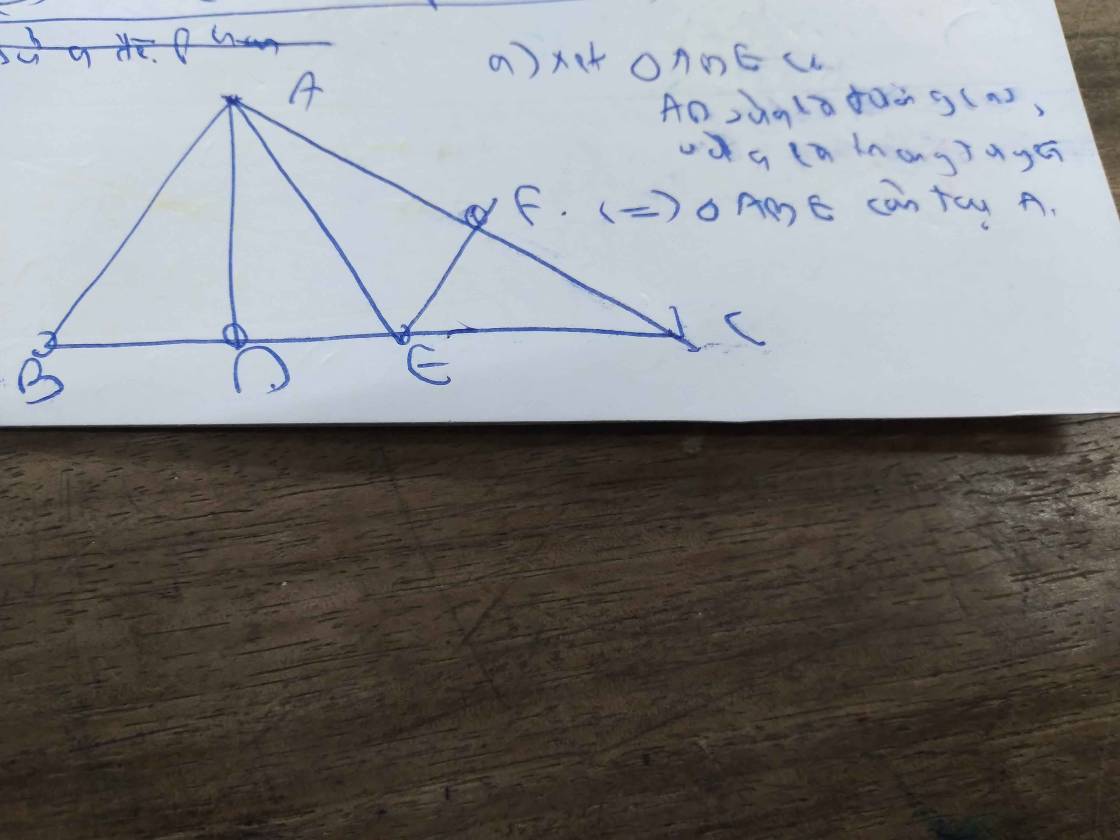
Cho tam giác nhọn ABC có AB>ACm đường cao AD. Trên đoạn DC lấy điểm E sao cho DB=DE.
a) Chứng minh tam giác ABE cân
b) Từ E kẻ EF vuông góc với AC(F thuộc AC). Từ C kẻ CK vuông góc với AE(K thuộc AE). Chứng minh ba đường thẳng AD, EF và CK đồng quy.

Những câu hỏi liên quan
Cho tam giác nhọn ABC có AB>ACm đường cao AD. Trên đoạn DC lấy điểm E sao cho DB=DE. a) Chứng minh tam giác ABE cân b) Từ E kẻ EF vuông góc với AC(F thuộc AC). Từ C kẻ CK vuông góc với AE(K thuộc AE). Chứng minh ba đường thẳng AD, EF và CK đồng quy.
a: Xét ΔABE có
AD vừa là đường cao, vừa là trung tuyến
=>ΔABE cân tại A
b: Gọi M là giao của AD và FE
Xét ΔAME có
ED,AF là đường cao
ED cắt AF tại C
=>C là trực tâm
=>M,C,K thẳng hàng
=>ĐPCM
Đúng 1
Bình luận (0)
Cho tam giác ABC có AB<AC, đường cao AD. Trên đoạn DC lấy E sao cho DB=DE
a) chứng minh tam giác ABE cân
b) từ E kẻ EF vuông góc với AC( F thuộc AC). Từ C kẻ CK đồng quy tại một điểm
Bài 1: Cho tam giác ABC có CA CB 10 cm AB 12 cm. Kẻ CI vuông góc với AB (I thuộc AB )a,chứng minh rằng IAIBb, Tính độ dài ICc, Kẻ IH vuông với AC (H thuộc AC) kẻ IK vuông góc với BC (K thuộc BC).So sánh các độ dài IH và IKBài 2: cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho ADAEa, chứng minh rằng BECDb, chứng minh rằng góc ABE bằng góc ACDc, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao?Bài 3: Cho tam giác ABC vuông ở C, có góc A b...
Đọc tiếp
Bài 1: Cho tam giác ABC có CA = CB = 10 cm AB = 12 cm. Kẻ CI vuông góc với AB (I thuộc AB )
a,chứng minh rằng IA=IB
b, Tính độ dài IC
c, Kẻ IH vuông với AC (H thuộc AC) kẻ IK vuông góc với BC (K thuộc BC).So sánh các độ dài IH và IK
Bài 2: cho tam giác ABC cân tại A. Trên cạnh AB lấy điểm D. Trên cạnh AC lấy điểm E sao cho AD=AE
a, chứng minh rằng BE=CD
b, chứng minh rằng góc ABE bằng góc ACD
c, Gọi K là giao điểm của BE và CD. Tam giác KBC là tam giác gì? Vì sao?
Bài 3: Cho tam giác ABC vuông ở C, có góc A bằng 60 độ tia phân giác của góc BAC cắt BC ở E kẻ CK vuông góc với AB (K thuộc AB) kẻ BD vuông góc với tia AE (D thuộc tia AE)chứng minh:
a, AC=AK và AE vuông góc CK
b,KB=KA
c, EB > AC
d, ba đường AC,BD,KE cùng đi qua 1 điểm
Bài 4: Cho tam giác nhọn ABC vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE .Gọi M là giao điểm của DC và BE Chứng minh rằng:
a, tam giác ABE=tam giác ADC
b,góc BMC=120°
Bài 5: Cho tam giác ABC vuông ở C ,có góc A bằng 60 độ tia phân giác của góc BAC cắt BC ở E,kẻ EK vuông góc với AB( K thuộc AB)kẻ BD vuông góc với AE (D thuộc AE) chứng minh
a,AK=KB
b, AD=BC
C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
Đúng 0
Bình luận (0)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm
Đúng 0
Bình luận (0)
Cho tam giác ABC có ABAC5cm, BC8cm. Kẻ AH vuông góc với BC (H thuộc BC)a, Chứng minh: HBHC và BAHCAHb, Tính độ dài AHc, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cânBài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BMCNa, Chứng minh: tam giác ABM tam giác ACNb, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AHAKc, Gọi O là giao điểm của HB v...
Đọc tiếp
Cho tam giác ABC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC)
a, Chứng minh: HB=HC và BAH=CAH
b, Tính độ dài AH
c, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
Bài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN
a, Chứng minh: tam giác ABM = tam giác ACN
b, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AH=AK
c, Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho tam giác ABC, kẻ BE vuông góc với AC và CF vuông góc với AB. Biết BE=CF=8 cm. Độ dài các đoạn thẳng BF và BC tỉ lệ với 3 và 5.
a, Chứng minh tam giác ABC là tam giác cân
b, Tính độ dài cạnh đáy BC
c, BE và CF cắt nhau tại O. Nối OA và EF. Chứng minh đường thẳng OA là trung trực của đoạn thẳng EF
Bài 5 : Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC (D thuộc AC). Từ D kẻ DE vuông góc với BC tại E. Gọi I là giao điểm của AE và BD. Chứng minh:
a, Tam giác ADB= tam giác EDB
b, BD là đường trung trực của AE
c, Tam giác EDC vuông cân
d, Lấy F thuộc tia đối của tia AB sao cho AF=EC.Chứng minh 3 điểm E, D, F thẳng hàng
Bài 6: Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm E, trên cạnh MP lấy điểm F sao cho ME=MF. Gọi S là giao điểm của NF và PE. Chứng minh
a, Tam giác MNF= tam giác MPE
b, Tam giác NSE= tam giác PSE
c, EF // NP
d, Lấy K là trung điểm của NP. Chứng minh ba điểm M, S, K thẳng hàng
Bài 7: Cho tam giác ABC vuông tại A. Trên BC lấy E sao cho BE=AB. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại D
a, Chứng minh AD=AE và góc ABD= góc EBD
b, Lấy điểm F thuộc tia đối của tia AB sao cho AF=EC. Chứng minh tam giác DFC cân
c, Gọi O là giao điểm của BD và AE. Chứng minh BD là đường trung trực của AE
d, Chứng minh 3 điểm F, D,E thẳng hàng
Mình đang cần gấp
Bài 3:
a: Xét ΔABM và ΔACN có
AB=AC
góc ABM=góc ACN
BM=CN
Do đó: ΔABM=ΔACN
Suy ra: AM=AN
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH=góc CAK
Do đó; ΔAHB=ΔAKC
Suy ra: AH=AK và BH=CK
c: Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
MB=CN
góc M=góc N
Do đó ΔHBM=ΔKCN
Suy ra: góc HBM=góc KCN
=>góc OBC=góc OCB
hay ΔOBC can tại O
Đúng 0
Bình luận (0)
Cho tam giác ABC có ABAC5cm, BC8cm. Kẻ AH vuông góc với BC (H thuộc BC)a, Chứng minh: HBHC và BAHCAHb, Tính độ dài AHc, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cânBài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BMCNa, Chứng minh: tam giác ABM tam giác ACNb, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AHAKc, Gọi O là giao điểm của HB và...
Đọc tiếp
Cho tam giác ABC có AB=AC=5cm, BC=8cm. Kẻ AH vuông góc với BC (H thuộc BC)
a, Chứng minh: HB=HC và BAH=CAH
b, Tính độ dài AH
c, Kẻ HD vuông góc với AB (D thuộc AB) , kẻ HE vuông góc với AC (E thuộc AC). Chứng minh tam giác HDE là tam giác cân
Bài 3: Cho tam giác ABC cân tại A. Trên tia đối của BC lấy điểm M, trên tia đối của CB lấy N sao cho BM=CN
a, Chứng minh: tam giác ABM = tam giác ACN
b, Kẻ BH vuông góc với AM, CK vuông góc với AN( H thuộc AM,K thuộc AN). Chứng minh : AH=AK
c, Gọi O là giao điểm của HB và KC. Tam giác OBC là tam giác gì? Vì sao?
Bài 4: Cho tam giác ABC, kẻ BE vuông góc với AC và CF vuông góc với AB. Biết BE=CF=8 cm. Độ dài các đoạn thẳng BF và BC tỉ lệ với 3 và 5.
a, Chứng minh tam giác ABC là tam giác cân
b, Tính độ dài cạnh đáy BC
c, BE và CF cắt nhau tại O. Nối OA và EF. Chứng minh đường thẳng OA là trung trực của đoạn thẳng EF
Bài 5 : Cho tam giác ABC vuông tại A, BD là tia phân giác của góc ABC (D thuộc AC). Từ D kẻ DE vuông góc với BC tại E. Gọi I là giao điểm của AE và BD. Chứng minh:
a, Tam giác ADB= tam giác EDB
b, BD là đường trung trực của AE
c, Tam giác EDC vuông cân
d, Lấy F thuộc tia đối của tia AB sao cho AF=EC.Chứng minh 3 điểm E, D, F thẳng hàng
Bài 6: Cho tam giác MNP cân tại M. Trên cạnh MN lấy điểm E, trên cạnh MP lấy điểm F sao cho ME=MF. Gọi S là giao điểm của NF và PE. Chứng minh
a, Tam giác MNF= tam giác MPE
b, Tam giác NSE= tam giác PSE
c, EF // NP
d, Lấy K là trung điểm của NP. Chứng minh ba điểm M, S, K thẳng hàng
Bài 7: Cho tam giác ABC vuông tại A. Trên BC lấy E sao cho BE=AB. Qua E kẻ đường thẳng vuông góc với BC cắt AC tại D
a, Chứng minh AD=AE và góc ABD= góc EBD
b, Lấy điểm F thuộc tia đối của tia AB sao cho AF=EC. Chứng minh tam giác DFC cân
c, Gọi O là giao điểm của BD và AE. Chứng minh BD là đường trung trực của AE
d, Chứng minh 3 điểm F, D,E thẳng hàng
Mình đang cần gấp
Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
Vì AH vuông góc với BC
Độ dài AH là 12
D€ABvaf E€Ac
Xem thêm câu trả lời
Cho tam giác ABC có AB < AC . Lấy E thuộc AC sao cho AE = AB. Trên tia đối của tia BA lấy điểm D sao cho BD = EC
a) Chứng minh tam giác ADC cân
b) Kẻ AH vuông góc với BE tại H , AH cắt DC tại K . Chứng minh AK là đường trung trực của DC
a) Ta có: AD=AB+BD(B nằm giữa A và D)
AC=AE+EC(E nằm giữa A và C)
mà AB=AE(gt)
và BD=CE(gt)
nên AD=AC
Xét ΔADC có AD=AC(cmt)
nên ΔADC cân tại A(Định nghĩa tam giác cân)
b) Xét ΔABE có AB=AE(gt)
nên ΔABE cân tại A(Định nghĩa tam giác cân)
Ta có: ΔABE cân tại A(cmt)
nên \(\widehat{ABE}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔABE cân tại A)(1)
Ta có: ΔADC cân tại A(cmt)
nên \(\widehat{ADC}=\dfrac{180^0-\widehat{A}}{2}\)(Số đo của một góc ở đáy trong ΔADC cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{ABE}=\widehat{ADC}\)
mà \(\widehat{ABE}\) và \(\widehat{ADC}\) là hai góc ở vị trí đồng vị
nên BE//DC(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: BE//DC(cmt)
BE\(\perp\)AK(gt)
Do đó: AK\(\perp\)DC(Định lí 2 từ vuông góc tới song song)
Ta có: ΔADC cân tại A(cmt)
mà AK là đường cao ứng với cạnh đáy DC(cmt)
nên AK là đường trung trực của DC(Định lí tam giác cân)(Đpcm)
Đúng 1
Bình luận (0)
a) Ta có: AD=AB+BD(B nằm giữa A và D)
AC=AE+EC(E nằm giữa A và C)
mà AB=AE(gt)
và BD=CE(gt)
nên AD=AC
Xét ΔADC có AD=AC(cmt)
nên ΔADC cân tại A(Định nghĩa tam giác cân)
b) Xét ΔABE có AB=AE(gt)
nên ΔABE cân tại A(Định nghĩa tam giác cân)
Ta có: ΔABE cân tại A(cmt)
nên ˆADC=1800−ˆA2ADC^=1800−A^2(Số đo của một góc ở đáy trong ΔADC cân tại A)(2)
Từ (1) và (2) suy ra ˆABE=ˆADCABE^=ADC^
mà ˆABEABE^ và ˆADCADC^ là hai góc ở vị trí đồng vị
nên BE//DC(Dấu hiệu nhận biết hai đường thẳng song song)
Ta có: BE//DC(cmt)
BE⊥⊥AK(gt)
Do đó: AK⊥⊥DC(Định lí 2 từ vuông góc tới song song)
Ta có: ΔADC cân tại A(cmt)
mà AK là đường cao ứng với cạnh đáy DC(cmt)
nên AK là đường trung trực của DC(Định lí tam giác cân)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại a, đường phân giác BD, kẻ DE vuông góc với BC (E thuộc BC). Chứng minh:
a)Tam giác ABD=tam giác EBD;
b)so sánh DA và DB;
c)BD vuông góc với AE;
d)AD<DC;
e)Kẻ CK vuông góc với BD(K thuộc BD). Chứng minh ED,CK,AB cùng đi qua một điểm.
Giúp em với ạ. Cho tam giác ABC vuông ở A, có AC = 2AB. Trong nửa mặt phẳng bờ AB có chứa C, dựng đoạn thẳng BD vuông góc AB và BD = AB. Từ điểm E tùy ý thuộc đoạn BD, kẻ đường thẳng vuông góc với AE cắt DC ở F. Chứng minh AE = EF.
Xem chi tiết
Cho tam giác ABC vuông tại A (AB < AC) kẻ AK vuông góc với BC tại K. Trên cạnh AC lấy điểm E sao cho AE = AB, từ E kẻ EF vuông với BC tại F .Chứng minh tam giác KAF vuông cân.