b1:Tìm điều khác biệt của pt sau:
2/x(x-3) - 1/x=x+3/x-3

Những câu hỏi liên quan
Tìm điều kiện xác định của pt và giải hệ pt sau :
x2- căn (1-x) = căn ( x-2 ) + 3
\(x-\sqrt{1-x}=\sqrt{x-2}+3\)
\(ĐK:\left\{{}\begin{matrix}1-x\ge0\\x-2\ge0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\le1\\x\ge2\end{matrix}\right.\Leftrightarrow x\in\varnothing\)
Vậy PT vô nghiệm
Đúng 1
Bình luận (0)
3.3. Cho pt: x ^ 2 - 4x + m = 0 (1). a) Tìm điều kiện của m để pt (1) có hai nghiệm phân biệt . b) Giải pt (1) với m = 3 .
Lời giải:
a. Để pt có 2 nghiệm phân biệt thì: $\Delta'=(-2)^2-m>0$
$\Leftrightarrow 4-m>0$
$\Leftrightarrow m< 4$
b. Với $m=3$ thì pt trở thành: $x^2-4x+3=0$
$\Leftrightarrow (x-1)(x-3)=0$
$\Leftrightarrow x-1=0$ hoặc $x-3=0$
$\Leftrightarrow x=1$ hoặc $x=3$
Đúng 0
Bình luận (0)
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 1 nghiệm phân biệt
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 2 nghiệm phân biệt
Tìm m để pt : (x2- x - m)\(\sqrt{x}\) = 0 có 3 nghiệm phân biệt
ĐKXĐ: \(x\ge0\)
\(\left(x^2-x-m\right)\sqrt{x}=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-x-m=0\left(1\right)\end{matrix}\right.\)
Giả sử (1) có nghiệm thì theo Viet ta có \(x_1+x_2=1>0\Rightarrow\left(1\right)\) luôn có ít nhất 1 nghiệm dương nếu có nghiệm
Do đó:
a. Để pt có 1 nghiệm \(\Leftrightarrow\left(1\right)\) vô nghiệm
\(\Leftrightarrow\Delta=1+4m< 0\Leftrightarrow m< -\dfrac{1}{4}\)
b. Để pt có 2 nghiệm pb
TH1: (1) có 1 nghiệm dương và 1 nghiệm bằng 0
\(\Leftrightarrow m=0\)
TH2: (1) có 2 nghiệm trái dấu
\(\Leftrightarrow x_1x_2=-m< 0\Leftrightarrow m>0\)
\(\Rightarrow m\ge0\)
c. Để pt có 3 nghiệm pb \(\Leftrightarrow\) (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=1+4m>0\\x_1x_2=-m>0\\\end{matrix}\right.\) \(\Leftrightarrow-\dfrac{1}{4}< m< 0\)
Đúng 3
Bình luận (0)
B1,Giải pt
a,X^2+x+4/2. + x^2+x+7/3.=x^2+x+13/5. + x^2+x+16/6
b,2/x^2+4x+3. + 5/x^2+11x+24. + 2/x^2+18x+80=9/25
B2,Cho pt ẩn x:x+m/x+3 +x-3/x-1=2 tìm các giá trị của tham số m để x=2
Cho PT: \(x^3-3x^2+\left(4m+3\right)x-8m-2=0\left(1\right)\)
a) Tìm m để pt(1) có 3 nghiệm phân biệt.
b) Khi pt(1) có 3 nghiệm phân biệt x1;x2;x3, tìm m để:x12+x22+x32=2017.
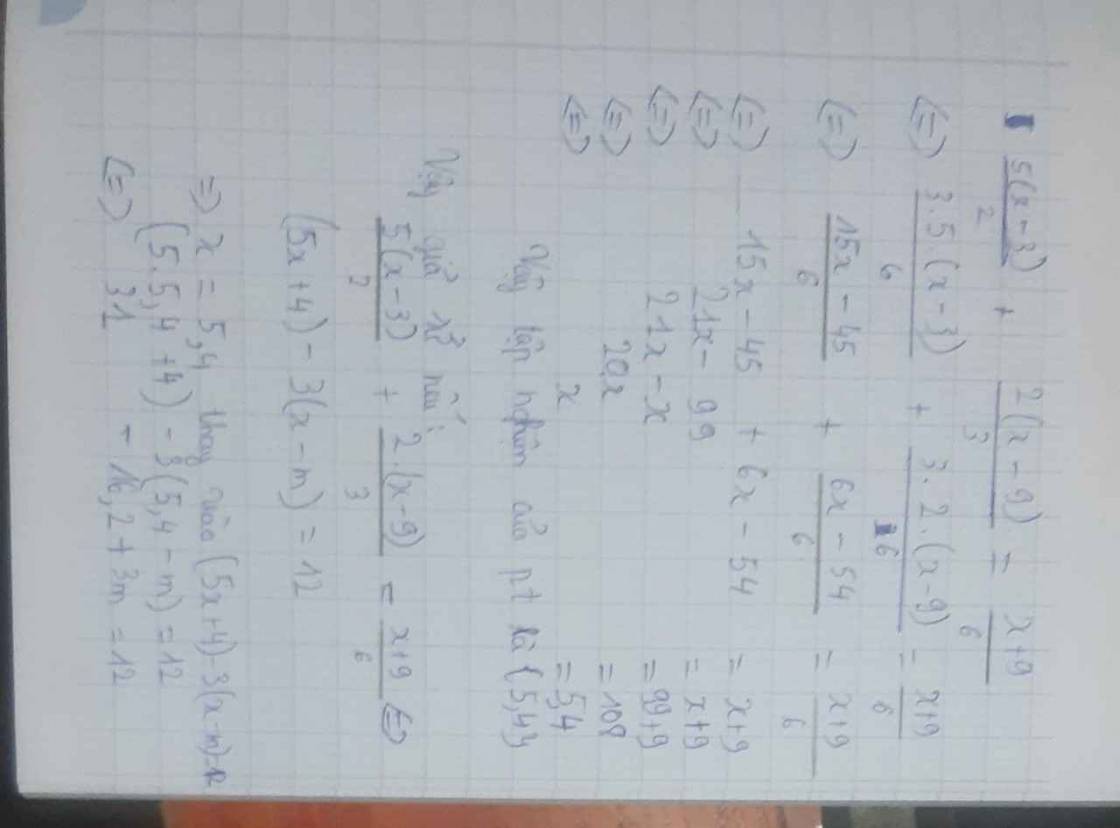
B1; Tìm m để hai pt sau tương đương\(\frac{5\left(x-3\right)}{2}+\frac{2\left(x-9\right)}{3}=\frac{x+9}{6}\) và (5x+4) -3(x-m)=12
cho pt x^3-5x^2+(2m+5)x-4m+2=0
a) tìm điều kiện của m để pt trên có 3 nghiệm phân biệt
b) tìm m để \(x_1^2+x_2^2+x_3^{2=11}\)
Nhẩm nghiệm ta được x = 2 là nghiệm của pt
Theo sơ đồ Hoc-ne ta được: x3 - 5x2 + (2x + 5)x - 4m + 2 = (x - 2)(x2 - 3x + 2m - 1) = 0
Đặt x2 - 3x + 2m - 1 là pt (*)
Để pt đề cho có 3 nghiệm phân biệt thì pt (*) có 2 nghiệm phân biệt khác 2
\(\Rightarrow\hept{\begin{cases}\Delta>0\\2^2-3.2+2m-1\ne0\end{cases}\Rightarrow\hept{\begin{cases}13-8m>0\\2m-3\ne0\end{cases}\Rightarrow}\hept{\begin{cases}m< \frac{13}{8}\\m\ne\frac{3}{2}\end{cases}}}\)
Vậy \(m< \frac{13}{8}\) và \(m\ne\frac{3}{2}\) thì pt đề cho có 3 nghiệm phân biệt
Đúng 0
Bình luận (0)
bài này chắc chỉ phân tích nhân tử,,,đưa ra 1 pt bặc 2 trong ngoặc rồi giải dental
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
: x^2 – 2( m- 1)x – 4m = 0 ( 3)
⦁ Tìm m để PT(3) có nghiệm
⦁ Tìm m để PT(3) có 2 nghiệm phân biệt
help voi mn
*, Để pt (3) có nghiệm
\(\Delta'=\left(m-1\right)^2-\left(-4m\right)=m^2+2m+1=\left(m+1\right)^2\ge0\)
Vậy pt luôn có 2 nghiệm x1 ; x2
*, \(\Delta'=\left(m+1\right)^2\ge0\)
Để pt có 2 nghiệm pb khi \(m+1\ne0\Leftrightarrow m\ne-1\)
Vậy với m khác -1 thì pt (3) luôn có 2 nghiệm pb
Đúng 2
Bình luận (0)
1,Tìm m để pt có \(\sqrt{2x^2+mx}=3-x\)
a, 1 nghiệm
b, 2 nghiệm phân biệt
2,Tìm m để pt có 2 nghiệm phân biệt \(\sqrt{x+2}+\sqrt{6-x}-\sqrt{\left(x+2\right)\left(6-x\right)}=m\)