Cho góc xOy= 135o ; kẻ đường thẳng z,z vuông góc với Ox tại O và t,t vuông góc với Oy tại O sao cho các tia Ot,Oz nằm trong góc xOy.
Chứng minh rằng Oz là tia phân giác của góc tOy.
Vẽ từng hình theo mỗi cách diễn đạt sau: Hai góc xOy và yOz kề bù, với ∠(xOy) = 135o.
Trên cùng một nửa mặt phẳng bờ chứa tia Ox, vẽ ba tia Oy, Oz và Ot sao cho số đo góc xOy bằng 45o, số đo góc xOz bằng 90o , số đo góc xOt bằng 135o
a, Tính số đo các góc yOz và yOt.
b, Tia Oz có phải là tia phân giác của góc yOt không? Vì sao?
Giải
a, Trên cùng một nửa mp bờ chứa tia Ox có \(xOy< xOz\left(45< 90\right)\)nên tia Oy nằm giữa hai tia Ox và Oz.Ta có:
\(xOy+yOz=xOz\)
\(45+yOz=90\)
\(\Rightarrow yOz=90-45=45\)
Trên cùng một nửa mp bờ chứa tia Ox có\(xOy< xOt\left(45< 135\right)\)nên tia Oy nằm giữa hai tia Ox và Ot.Ta có:
\(xOy+yOt=xOt\)
\(45+yOt=135\)
\(\Rightarrow yOt=135-45=90\)
b, Trên cùng một nửa mp bờ chứa tia Ox có \(xOz< xOt\left(90< 135\right)\)nên tia Oz nằm giữa hai tia Ox và Ot.Ta có:
\(xOz+zOt=xOt\)
\(90+zOt=135\)
\(\Rightarrow zOt=135-90=45\)
Trên cùng một nửa mp bờ chứa tia Oy có \(yOz< yOt\left(45< 90\right)\)nên tia Oz nằm giữa hai tia Oy và Ot
Vì tia Oz nằm giữa hai tia Oy và Ot lại có:\(yOz=zOt\left(=45\right)\)nên tia Oz là tia phân giác của \(yOt\)
k mình với
Vẽ: Góc 135o.
Vẽ tia Oa Đặt thước đo góc sao cho tâm của thước trùng với gốc O của tia Oa và tia Oa đi qua vạch 0o của thước.
- Vẽ tia Ob đi qua vạch 135o của thước đo góc, ta có góc aOb = 135o
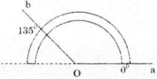
Số đo radian của góc 135o là:
A. π 6
B. π 3
C. 3 π 4
D. π 4
Vẽ góc IKM có số đo bằng 135o
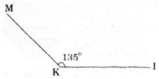
- Cách vẽ:
+ Vẽ tia KI.
+ Đặt thước đo góc sao cho tâm của thước trùng với góc K của tia KI và tia KI đi qua vạch 0o.
+ Vẽ tia KM đi qua vạch 135 của thước. Ta vẽ được góc IKM = 135o
cho góc AOB bằng 135o .tia OC nằm trong góc AOB .biết góc AOC bằng 1/2 góc COB: a)Tính số đo góc b)xác định loại góc của 3 góc sau: góc AOB;góc BOC; góc COA
Cho góc AOB = 135o , C là một điểm nằm trong góc AOB , biết góc BOC = 90o a) Tính \(\widehat{AOC}\)
b) Gọi OD là tia đối của tia OC . So sánh \(\widehat{AOD}\) và \(\widehat{BOD}\)
Cho tam giác ABC có ∠A = ∠B + ∠C . Hai đường phân giác của góc A và góc C cắt nhau tại O. Khi đó BOC bằng:
(A) 85o ;
(B) 90o ;
(C) 135o ;
(D) 150o
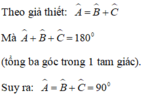
Do AO, CO lần lượt là tia phân giác của ∠A và ∠C nên BO là tia phân giác của ∠B
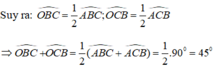
Xét tam giác OBC có:
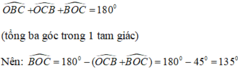
Chọn (C) 135º.
Tính diện tích hình bình hành ABCD biết góc Â= 135o ,AD= √2 dm, CD= 3 dm
Theo tính chất hình bình hành, \(\widehat{A}+\widehat{D}=180^0\Rightarrow\widehat{D}=45^0\)
Từ A kẻ AH vuông góc CD
Trong tam giác vuông ADH: \(\widehat{D}+\widehat{DAH}=90^0\Rightarrow\widehat{DAH}=45^0\)
\(\Rightarrow\widehat{DAH}=\widehat{D}\Rightarrow\Delta DAH\) vuông cân tại H \(\Rightarrow AH=DH\)
Áp dụng Pitago:
\(AH^2+DH^2=AD^2\Rightarrow2AH^2=2\)
\(\Rightarrow AH=1\)
\(\Rightarrow S_{ABCD}=AH.CD=1.3=3\left(dm^2\right)\)
Tính diện tích hình bình hành ABCD biết góc Â= 135o ,AD= √2 dm, CD= 3 dm