Thay x = 2 ; y = m vào hàm số  y = 1 4 x 2

ta được  m = 1 4 . 2 2 = 1 2

Vậy  m = 1 2

Đáp án cần chọn là: A

Thay x = m 5 ; y = −2 5 vào hàm số  y = − 5 x 2 ta được

− 2 5 = − 5 . m 5 2 ⇔ − 5 m 5 = 2 5 ⇔ m = − 2 5

Vậy  m = − 2 5

Đáp án cần chọn là: D

Phương trình hoành độ giao điểm là:

\(-\dfrac{1}{4}x^2-mx-n=0\)

THeo đề, ta có:

\(\left\{{}\begin{matrix}m+n=2\\\left(-m\right)^2-4\cdot\left(-\dfrac{1}{4}\right)\cdot\left(-n\right)=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\m^2-n=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}m=2-n\\n^2-4n+4-n=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}n\in\left\{1;4\right\}\\m\in\left\{1;-2\right\}\end{matrix}\right.\)

kiểm tra lại đề nhé lỗi quá

parabol (P): y =  x 2  ; đường thẳng (d): y = 2x + m (m là tham số).

a) phương trình hoành độ giao điểm của (P) và (d) là:

x 2  = 2x + m ⇔  x 2 - 2x - m = 0

Δ'= 1 + m

(d) tiếp xúc với (P) khi phương trình hoành độ giao điểm có duy nhất 1 nghiệm

⇔ Δ'= 1 + m = 0 ⇔ m = -1

Khi đó hoành độ giao điểm là x = 1

a: 

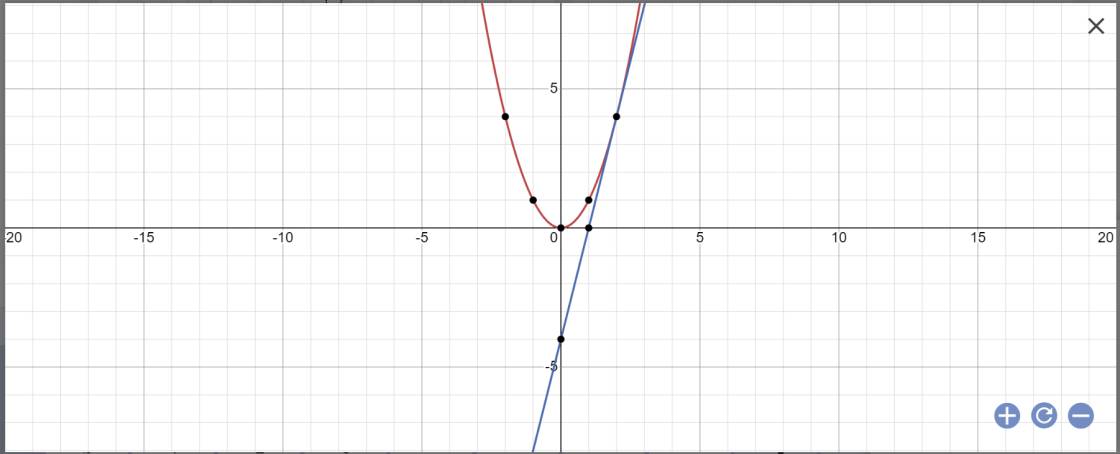
b: PTHĐGĐ là:

2x^2-(2m-2)x+m-1=0

Δ=(2m-2)^2-4*2*(m-1)

=4m^2-8m+4-8m+8

=4m^2-16m+12

=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)

Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0

=>m>3 hoặc m<1

Đường thẳng y = mx + n đi qua điểm A ( -1 ; -2 ) nên 

-2 = -m + n ,suy ra n = m-2 

Phương trình đường thẳng có dạng y = mx + ( m -2 ) .Điều kiện để đường thẳng tiếp xúc với parabol là phương trình \(\frac{x^2}{4}=mx+\left(m-2\right)\)        (1) 

có nghiệm kép .Biến đổi (1) ta được : x² -4.m.x - 4. ( m-2) =0          (2) 

Điều kiện để ( 1 ) cũng có nghĩa là ( 2 ) có nghiệm kép là : 

\(\Delta'=4m^2+4m-8=0\Leftrightarrow m^2+m-2=0\)

<=> ( m+2 ) . ( m-1 ) = 0 <=> m =-2 hoặc m = 1 .

Vậy các hệ số m , ncaanf tìm là m = -2 ; n = -4 và m =1 ; n=-1 

a, Thay m = -1/2 vào (d) ta được : 

\(y=2x-2.\left(-\frac{1}{2}\right)+2\Rightarrow y=2x+3\)

Hoành độ giao điểm thỏa mãn phương trình 

\(2x+3=x^2\Leftrightarrow x^2-2x-3=0\)

\(\Delta=4-4\left(-3\right)=4+12=16>0\)

\(x_1=\frac{2-4}{2}=-1;x_2=\frac{2+4}{2}=3\)

Vói x = -1 thì \(y=-2+3=1\)

Vớ x = 3 thì \(y=6+3=9\)

Vậy tọa độ giao điểm của 2 điểm là A ( -1 ; 1 ) ; B ( 3 ; 9 )

b, mình chưa học 

\(y_1+y_2=4\left(x_1+x_2\right)\)

\(\Leftrightarrow x_1^2+x_2^2=4\left(x_1+x_2\right)\)(1)

Xét phương trình hoành độ giao điểm của (d) và (P) ta có: 

\(x^2=2x-2m+2\)

\(\Leftrightarrow x^2-2x+2m-2=0\)

Theo hệ thức Vi-et ta có: 

\(\hept{\begin{cases}x_1+x_2=2\\x_1x_2=2m-2\end{cases}}\)

Từ (1)  \(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4\left(x_1+x_2\right)\)

\(\Leftrightarrow4-4m+4=8\)

\(\Leftrightarrow m=0\)

vậy..

sửa lại hoàn chỉnh cho câu a nhé んuﾘ ｲ ( ✎﹏IDΣΛ亗 )  e mới học a ko trách đâu nhưng đi thi làm thế này trừ bị điểm

a) Xét phương trình hoành độ giao điểm chung của (d) và (P) :

\(x^2=2x-2m+2\)

\(\Leftrightarrow x^2-2x+2m-2=0\)

Thay m=\(\frac{-1}{2}\)vào ...

đến đây delta trình bày như e đc r 

b) Cấn Minh Vy  câu a có pt giao điểm chung  rồi thì câu b ko cần đâu bỏ đi nha, chả qua mình viết thế để tách bài riêng biệt

a: Thay x=2 vào (P),ta được:

y=2^2/2=2

2: Thay x=2 và y=2 vào (d), ta được:

m-1+2=2

=>m-1=0

=>m=1