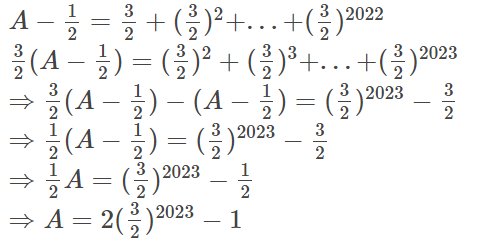A =                 \(\dfrac{1}{2}+\dfrac{3}{2}+\dfrac{3}{2^2}+\dfrac{3}{2^3}+.....+\dfrac{3}{2^{2021}}+\dfrac{3}{2^{2022}}\)

     \(2\times\)A =             1 + 3+   \(\dfrac{3}{2}\) +\(\dfrac{3}{2^2}\)  + \(\dfrac{3}{2^3}\)+...........+\(\dfrac{3}{2^{2021}}\)

2 \(\times\) A - A =           4 - \(\dfrac{1}{2}\) - \(\dfrac{3}{2^{2022}}\)

             A =          \(\dfrac{7}{2}\)    - \(\dfrac{3}{2^{2022}}\)

            B =                  2 \(\times\dfrac{3}{2^{2023}}\)

      A - B  =         \(\dfrac{7}{2}-\dfrac{3}{2^{2022}}\)  - 2 \(\times\) \(\dfrac{3}{2^{2023}}\)

     A - B =           \(\dfrac{7}{2}\)   - \(\dfrac{3}{2^{2022}}\) - \(\dfrac{3}{2^{2022}}\)

    A - B =            \(\dfrac{7}{2}\) - \(\dfrac{6}{2^{2022}}\)

   A - B =            \(\dfrac{7}{2}\) - \(\dfrac{3}{2^{2021}}\)

Lời giải:

$\Rightarrow A-B=-1$

hảo hán nào giải đc không vậy?

quên cách làm rùi

ủa cái j dợ

Sửa đề: \(a=\frac13-\frac{2}{3^2}+\frac{3}{3^3}-\frac{4}{3^4}+\cdots+\frac{2023}{3^{2023}}-\frac{2024}{3^{2024}}\)

Ta có: \(a=\frac13-\frac{2}{3^2}+\frac{3}{3^3}-\frac{4}{3^4}+\cdots+\frac{2023}{3^{2023}}-\frac{2024}{3^{2024}}\)

=>\(3a=1-\frac23+\frac{3}{3^2}-\frac{4}{3^3}+\cdots+\frac{2023}{3^{2022}}-\frac{2024}{3^{2023}}\)

=>\(3a+a=1-\frac23+\frac{3}{3^2}-\frac{4}{3^3}+\cdots+\frac{2023}{3^{2022}}-\frac{2024}{3^{2023}}+\frac13-\frac{2}{3^2}+\frac{3}{3^3}-\frac{4}{3^4}+\cdots+\frac{2023}{3^{2023}}-\frac{2024}{3^{2024}}\)

=>\(4a=1-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\cdots-\frac{1}{3^{2023}}-\frac{2024}{3^{2024}}\)

Đặt \(b=-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\cdots-\frac{1}{3^{2023}}\)

=>\(3b=-1+\frac13-\frac{1}{3^2}+\cdots-\frac{1}{3^{2022}}\)

=>\(3b+b=-1+\frac13-\frac{1}{3^2}+\cdots-\frac{1}{3^{2022}}-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\cdots-\frac{1}{3^{2023}}\)

=>\(4b=-1-\frac{1}{3^{2023}}=\frac{-3^{2023}-1}{3^{2023}}\)

=>\(b=\frac{-3^{2023}-1}{4\cdot3^{2023}}\)

Ta có: \(4a=1-\frac13+\frac{1}{3^2}-\frac{1}{3^3}+\cdots-\frac{1}{3^{2023}}-\frac{2024}{3^{2024}}\)

=>\(4a=1+\frac{-3^{2023}-1}{4\cdot3^{2023}}-\frac{2024}{3^{2024}}=1+\frac{-3^{2024}-3}{4\cdot3^{2024}}-\frac{8096}{4\cdot3^{2024}}\)

=>\(4a=1-\frac{3^{2024}+8099}{4\cdot3^{2024}}=1-\frac14-\frac{8099}{4\cdot3^{2024}}=\frac34-\frac{8099}{4\cdot3^{2024}}\)

=>\(4a<\frac34\)

=>\(a<\frac{3}{16}\)

mà \(\frac{3}{16}<1<\frac{20}{3}\)

nên \(a<\frac{20}{3}\)

A=223​+328​+4215​+...+2023220232−1​

\(A = \frac{2^{2} - 1}{2^{2}} + \frac{3^{2} - 1}{3^{2}} + \frac{4^{2} - 1}{4^{2}} + . . . + \frac{202 3^{2} - 1}{202 3^{2}}\)

\(A = 1 - \frac{1}{2^{2}} + 1 - \frac{1}{3^{2}} + 1 - \frac{1}{4^{2}} + . . . + 1 - \frac{1}{202 3^{2}}\)

\(A = \left(\right. 1 + 1 + 1 + . . . + 1 \left.\right) - \left(\right. \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + . . + \frac{1}{202 3^{2}} \left.\right)\)

Tổng số hạng của 2 ngoặc trên bằng nhau và =(2023-2):1+1=2022(số hạng)

\(A = 2022 - \left(\right. \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + . . . + \frac{1}{202 3^{2}} \left.\right)\)

Ta thấy:

\(0 < \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4^{2}} + . . . + \frac{1}{202 3^{2}} < \frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + . . + \frac{1}{2022.2023}\)

Ta có

\(\frac{1}{1.2} + \frac{1}{2.3} + \frac{1}{3.4} + . . + \frac{1}{2022.2023}\)

\(= 1 - \frac{1}{2} + \frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + . . + \frac{1}{2022} - \frac{1}{2023}\)

\(= 1 - \frac{1}{2023} < 1\)

Do đó,2021<A<2022 

Vậy giá trị của A không phải 1 số tự nhiên(đpcm)

$A=\frac{3}{2^2}+\frac{8}{3^2}+\frac{15}{4^2}+....+\frac{{2023}^2-1}{{2023}^2}$

$A=1-\frac{1}{2^2}+1-\frac{1}{3^2}+1-\frac{1}{4^2}+....+1-\frac{1}{{2023}^2}$

$A=2022-(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{{2023}^2})$

$\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{{2023}^2}<\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2022.2023}$

$\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2022.2023}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+....-\frac{1}{2023}$

$\Rightarrow 0<\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{{2023}^2}<1-\frac{1}{2023}<1$

$\Rightarrow 2022-(\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+...+\frac{1}{{2023}^2})$ko phải số tự nhiên

$\Rightarrow A$ ko phải số tự nhiên

322+832+1542+....+20232-120232"" id="MathJax-Element-1-Frame" role="presentation" tabindex="0" style="box-sizing: inherit; display: inline-table; line-height: 0; font-size: 18.08px; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">A=322+832+1542+....+20232−120232�=322+832+1542+....+20232-120232A=

1-122+1-132+1-142+....+1-120232"" id="MathJax-Element-2-Frame" role="presentation" tabindex="0" style="box-sizing: inherit; display: inline-block; line-height: 0; font-size: 18.08px; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">A=1−122+1−132+1−1(2+....+1)120232�=1-122+1-132+1-142+....+1-1202321+12+13+...+122023−1

2022-(122+132+142+...+120232)"" id="MathJax-Element-3-Frame" role="presentation" tabindex="0" style="box-sizing: inherit; display: inline-block; line-height: 0; font-size: 18.08px; overflow-wrap: normal; word-spacing: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; margin: 0px; padding: 1px 0px; position: relative;">A=2022−(122+132+142+...+120232)�=2022-(122+132+142+...+120232)A

k

3A=3+3^2+...+3^2024

=>2A=3^2024-1

=>B-2A=3^2023-3^2024+1

\(A=\dfrac{2}{3}+\dfrac{2}{3^2}+\dfrac{2}{3^3}+....+\dfrac{2}{3^{2023}}\)

\(3A=2+\dfrac{2}{3}+\dfrac{2}{3^2}+....+\dfrac{2}{3^{2022}}\)

\(3A-A=\left(2+\dfrac{2}{3}+\dfrac{2}{3^2}+...+\dfrac{2}{3^{2022}}\right)-\left(\dfrac{2}{3}+\dfrac{2}{3^2}+....+\dfrac{2}{3^{2023}}\right)\)

\(2A=2-\dfrac{2}{3^{2023}}\)

\(A=\left(2-\dfrac{2}{3^{2023}}\right)\times\dfrac{1}{2}\)

\(A=2\times\dfrac{1}{2}-\dfrac{2}{3^{2023}}\times\dfrac{1}{2}\)

\(A=1-\dfrac{1}{3^{2023}}\)

=> \(A< 1\left(đpcm\right)\)