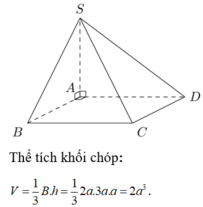
Cho hình chóp S.ABCD có ABCD là hình chữ nhật có tâm O, AB a AC=3a. SA vuông góc với mp (ABCD); SC-5a. a) Chứng minh BC l S4F. b) Trong tam giác SAD kẻ AH vuông góc SD. Chứng minh AH _ (SCD) c Xác định và tinh góc giữa SO và (SCD).

Những câu hỏi liên quan
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Cmr: CD vuông góc mp (SAD) b) Cmr: (SAC) vuông góc mp (SBD) c) Tính góc giữa SC v à mp (ABCD) d) Tính góc giữa mp ( SAB) và mp (SBC). e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O, AD = 2 ,AB = 4, SA= 2 và SA vuông góc với mp ( ABCD). Khoảng cách từ điểm O đến (SCD) bằng ?
Do \(OC=\dfrac{1}{2}AC\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}d\left(A;\left(SCD\right)\right)\)
Kẻ \(AH\perp SD\Rightarrow AH\perp\left(SCD\right)\)
\(\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{SA.AD}{\sqrt{SA^2+AD^2}}=\sqrt{2}\)
\(\Rightarrow d\left(O;\left(SCD\right)\right)=\dfrac{1}{2}AH=\dfrac{\sqrt{2}}{2}\)
Đúng 2
Bình luận (3)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật ACa căn 3, BC 2a, SA vuông góc (ABCD), SA3a. Gọi O là giao điểm của AC và BD.a) Cmr: CD vuông góc mp (SAD)b) Cmr: (SAC) vuông góc mp (SBD)c) Tính góc giữa SC v à mp (ABCD)d) Tính góc giữa mp ( SAB) và mp (SBC).e) Tính khoảng cách từ A đến mp ( SBD)
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD.
a) Cmr: CD vuông góc mp (SAD)
b) Cmr: (SAC) vuông góc mp (SBD)
c) Tính góc giữa SC v à mp (ABCD)
d) Tính góc giữa mp ( SAB) và mp (SBC).
e) Tính khoảng cách từ A đến mp ( SBD)
a: CD vuông góc AD; CD vuông góc SA
=>CD vuông góc (SAD)
b: BD vuông góc AC; BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
c: (SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=căn 3
=>góc SCA=60 độ
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AC=a căn 3, BC = 2a, SA vuông góc (ABCD), SA=3a. Gọi O là giao điểm của AC và BD. a) Tính góc giữa mp ( SAB) và mp (SBC). b) Tính khoảng cách từ A đến mp ( SBD)
Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?
Đúng 0
Bình luận (1)
cho hình chóp S.ABCD có đáy abcd là hình chữ nhật tâm O, AD=4, AB=2, SA=2 và SA vuông góc (ABCD). tính góc hơp boi 2 đthg SO và mp(SAD)?
Gọi M là trung điểm AD \(\Rightarrow OM\perp AD\Rightarrow OM\perp\left(SAD\right)\)
\(\Rightarrow\widehat{MSO}\) là góc giữa SO và (SAD)
\(SM=\sqrt{SA^2+\left(\dfrac{AD}{2}\right)^2}=2\sqrt{2}\)
\(OM=\dfrac{1}{2}CD=1\)
\(tan\widehat{MSO}=\dfrac{OM}{SM}=\dfrac{1}{2\sqrt{2}}\) \(\Rightarrow\widehat{MSO}\approx19^028'\)
Đúng 2
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB a, BC 2a, SA 3a. Biết SA vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD là: A.
a
3
B.
2
a
3
C.
6
a
3
D.
12
a
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật AB = a, BC = 2a, SA = 3a. Biết SA vuông góc với mặt phẳng (ABCD). Thể tích khối chóp S.ABCD là:
A. a 3
B. 2 a 3
C. 6 a 3
D. 12 a 3
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết ABa, BC3a, SA2a.Tính thể tích V của khối chóp S.ABCD. A.
V
3
a
3
B.
V
2
a
3
C.
V
a
3
D.
V
6
a
3
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, cạnh bên SA vuông góc với đáy (ABCD). Biết AB=a, BC=3a, SA=2a.Tính thể tích V của khối chóp S.ABCD.
A. V = 3 a 3
B. V = 2 a 3
C. V = a 3
D. V = 6 a 3
Đáp án B
Thể tích khối chóp S.ABCD là:
V A B C D = 1 3 S A . S A B C D = 1 3 2 a .3 a 2 = 2 a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB a, AD 2a, SA 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD. A.
4
a
3
3
(đvtt) B.
4
a
3
(đvtt) C.
2
a
3
3
(đvtt) D.
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật, AB = a, AD = 2a, SA = 2a, SA vuông góc với mp(ABCD). Tính thể tích khối chóp S.ABCD.
A. 4 a 3 3 (đvtt)
B. 4 a 3 (đvtt)
C. 2 a 3 3 (đvtt)
D. 2 a 3 (đvtt)
Đáp án A
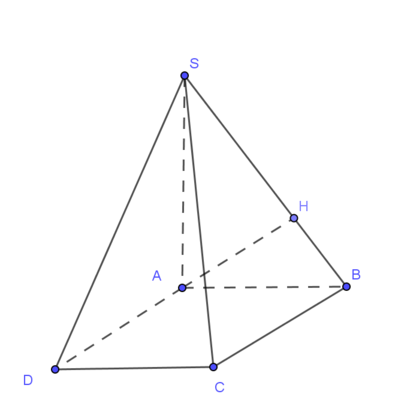
Ta có:
V S . A B C D = 1 3 S A . S A B C D = 1 3 .2 a . a .2 a = 4 3 a 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB 2a; AD 3a. Cạnh bên SA vuông góc với đáy ABCD và SA a. Tính thể tích V của khối chóp S.ABCD. A. V6a3 B. Va3 C. V3a3 D. V2a3.
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = 2a; AD = 3a. Cạnh bên SA vuông góc với đáy ABCD và SA = a. Tính thể tích V của khối chóp S.ABCD.
A. V=6a3
B. V=a3
C. V=3a3
D. V=2a3.