a: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)

Vì (d)//y=3x+2 nên \(\left\{{}\begin{matrix}a=3\\b\ne2\end{matrix}\right.\)

Vậy: (d): y=3x+b

Thay x=1 và y=2 vào (d), ta được:

\(b+3\cdot1=2\)

=>b+3=2

=>b=-1

vậy: (d): y=3x-1

b: Gọi phương trình đường thẳng cần tìm là (d): y=ax+b(a<>0)
Vì (d) có tung độ gốc là 3 nên b=3

=>(d): y=ax+3

Thay x=-4 và y=7 vào (d), ta được:

\(-4a+3=7\)

=>-4a=4

=>a=-1

vậy: (d): y=-x+3

c: A(1;4); B(4;8)

=>\(AB=\sqrt{\left(4-1\right)^2+\left(8-4\right)^2}\)

=>\(AB=\sqrt{3^2+4^2}=\sqrt{25}=5\)

c: y=2x-6

=>2x-y-6=0

Khoảng cách từ A(-3;2) đến đường thẳng 2x-y-6=0 là;

\(d\left(A;2x-y-6=0\right)=\dfrac{\left|\left(-3\right)\cdot2+2\left(-1\right)-6\right|}{\sqrt{2^2+\left(-1\right)^2}}\)

\(=\dfrac{\left|-6-2-6\right|}{\sqrt{5}}=\dfrac{14}{\sqrt{5}}\)

Giả sử đường thẳng ∆ song song với d : 3x- 4y+2= 0

Khi đó ; ∆ có phương trình là ∆ : 3x-4y +C= 0.

Lấy điểm  M( -2 ; -1) thuộc d.

Do đó ; 2 đường thẳng thỏa mãn là:3x – 4y + 7 = 0 và 3x – 4y – 3 = 0

Chọn B

a.

\(\overrightarrow{AB}=\left(1;2\right)\Rightarrow\) đường thẳng AB nhận (2;-1) là 1 vtpt

Phương trình AB:

\(2\left(x-1\right)-1\left(y+3\right)=0\Leftrightarrow2x-y-5=0\)

b.

d vuông góc \(\Delta\Rightarrow d\) nhận (4;-3) là 1 vtpt

Phương trình d có dạng: \(4x-3y+c=0\)

\(d\left(B;d\right)=\dfrac{\left|4.2-3.\left(-1\right)+c\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{2}{5}\)

\(\Leftrightarrow\left|c+11\right|=2\Rightarrow\left[{}\begin{matrix}c=-9\\c=-13\end{matrix}\right.\)

Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}4x-3y-13=0\\4x-3y-9=0\end{matrix}\right.\)

Đặt (d): y=ax+b

Hệ số góc là k=2 nên a=2

=>y=2x+b

=>2x-y+b=0

Khoảng cách từ O(0;0) đến (d) là \(2\sqrt{5}\) nên ta có:

\(\dfrac{\left|0\cdot2+0\cdot\left(-1\right)+b\right|}{\sqrt{2^2+\left(-1\right)^2}}=2\sqrt{5}\)

=>\(\left|b\right|=2\sqrt{5}\cdot\sqrt{5}=10\)

=>b=10 hoặc b=-10

=>(d): y=2x+10 hoặc y=2x-10

=>2x-y+10=0 hoặc 2x-y-10=0

\(1/\)

\(M\left(3;5\right);d:x+y+1=0\)

\(\)Gọi khoảng cách từ M đến d là \(l\)

\(l\left(M;d\right)=\dfrac{\left|x_M+y_M+1\right|}{\sqrt{1^2+1^2}}=\dfrac{\left|3+5+1\right|}{\sqrt{1^2+1^2}}=\dfrac{9\sqrt{2}}{2}\)

\(M\left(2;3\right);d:\left\{{}\begin{matrix}x-2t\\y=2+3t\end{matrix}\right.\)

d qua \(M\left(2;3\right)\) có \(VTCP\overrightarrow{u}=\left(-2;3\right)\Rightarrow VTPT\overrightarrow{n}=\left(3;2\right)\)

\(PTTQ\) của \(\Delta:3\left(x-2\right)+2\left(y-3\right)=0\)

\(\Rightarrow3x-6+2y-6=0\)

\(\Rightarrow3x+2y-12=0\)

Gọi khoảng cách từ M đến d là \(l\)

\(l\left(M;d\right)=\dfrac{\left|3.x_M+2.y_M-12\right|}{\sqrt{3^2+2^2}}=\dfrac{\left|3.2+2.3-12\right|}{\sqrt{3^2+2^2}}=0\)

Đáp án: C

Gọi d’ là đường thẳng song song với d và cách d một khoảng bằng 10

Vì d’//d nên d’ có dạng: 3x - y + c = 0, (c ≠ 1)

Lấy M(0;1) ∈ d. Vì d’ cách d một khoảng bằng 10 nên:

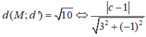
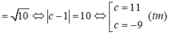
Vậy d': 3x - y + 11 = 0 hoặc d': 3x - y - 9 = 0