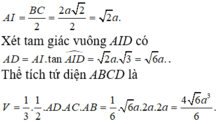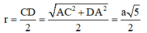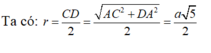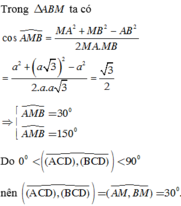Cho tứ diện ABCD có AB=2a; \(CD=2\sqrt{2}a\). M,N lần lượt là trung điểm của BC,AD. \(MN=a\sqrt{5}\). Tính số đo góc giữa hai đường thẳng AB và CD

Những câu hỏi liên quan
Cho tứ diện ABCD có ABACAD2a. Biết tam giác BCD có BC2a, BDa,
C
B
D
^
120
°
. Tính thể tích tứ diện ABCD theo a
Đọc tiếp
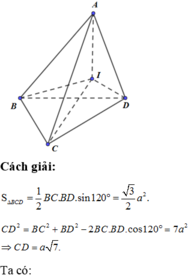
Cho tứ diện ABCD có AB=AC=AD=2a. Biết tam giác BCD có BC=2a, BD=a, C B D ^ = 120 ° . Tính thể tích tứ diện ABCD theo a
![]()
![]()
![]()
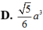
Cho tứ diện ABCD có AB AC AD 2a. Biết tam giác BCD có BC 2a, BD a,
C
B
D
^
120
0
. Tính thể tích tứ diện ABCD theo a. A.
5
3
a
3
B.
5
2
a
3...
Đọc tiếp
Cho tứ diện ABCD có AB = AC = AD = 2a. Biết tam giác BCD có BC = 2a, BD = a, C B D ^ = 120 0 . Tính thể tích tứ diện ABCD theo a.
A. 5 3 a 3
B. 5 2 a 3
C. 5 a 3
D. 5 6 a 3
Phương pháp:
Sử dụng các công thức diện tích tam giác ![]() và công thức Cosin
và công thức Cosin ![]()
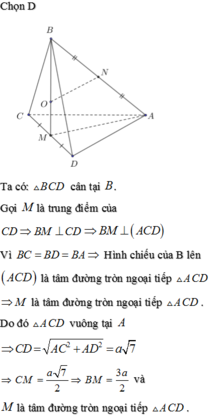
Cách giải:
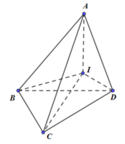
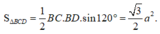
![]()
![]()
Ta có: ![]()
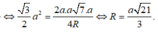
Gọi I là tâm đường tròn ngoại tiếp tam giác BCD.
Do AB = AC = AD ![]()
![]()
Thể tích tứ diện ABCD là 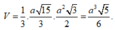
Chọn D.
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có ABBCACBD2a, AD
a
3
; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
Đọc tiếp
Cho tứ diện ABCD có AB=BC=AC=BD=2a, AD= a 3 ; hai mặt phẳng (ACD) và (BCD) vuông góc với nhau. Diện tích mặt cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng
A
B
A
C
2
a
và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng
60
0
.
Tính thể tích khối tứ diện ABCD. A.
2
6
a
3
3
B....
Đọc tiếp
Cho tứ diện ABCD có cạnh AB,AC,AD đôi một vuông góc. Biết rằng A B = A C = 2 a và góc tạo bởi hai mặt phẳng (DCB) và (ABC) bằng 60 0 . Tính thể tích khối tứ diện ABCD.
A. 2 6 a 3 3
B. 4 6 a 3 3
C. 2 6 a 3
D. 4 6 a 3
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD a, AC 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD. A.
r
a
5
B.
r
a
3
2
C. r a D.
r
a
5
2
Đọc tiếp
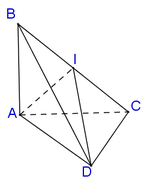
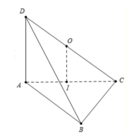
Cho tứ diện ABCD có DA vuông góc với (ABC) và AD = a, AC = 2a; cạnh BC vuông góc với cạnh AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Đáp án D
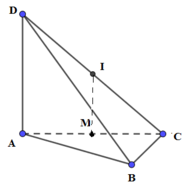
Phương pháp:
+) Xác định tâm mặt cầu ngoại tiếp khối tứ diện là điểm cách đều tất cả các đỉnh của tứ diện.
+) Áp dụng định lí Pytago tính bán kính mặt cầu ngoại tiếp tứ diện.
Cách giải:
Tam giác ABC vuông tại B, M là trung điểm của AC ⇒ M là tâm đường tròn ngoại tiếp tam giác ABC
Gọi I là trung điểm của CD ⇒ IC = ID(1)
Ta có: IM là đường trung bình của tam giác ACD ⇒ IM // AD
Mà AD ⊥ (ABC) ⇒ IM ⊥ (ABC)
Do đó, IM là trục đường tròn ngoại tiếp tam giác ABC
⇒ IA = IB = IC(2)
Từ (1), (2) ⇒ IA = IB = IC = ID ⇒ I là tâm mặt cầu ngoại tiếp tứ diện ABCD, bán kính mặt cầu:
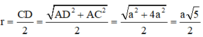
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD a, AC 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD. A.
r
a
5
B.
r
a
3
2
C. r a D.
r
a
5
2
Đọc tiếp
Cho tứ diện ABCD có DA vuông góc với mặt phẳng (ABC) và AD = a, AC = 2a. cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện ABCD.
A. r = a 5
B. r = a 3 2
C. r = a
D. r = a 5 2
Cho tứ diện
A
B
C
D
có DA vuông góc với mặt phẳng
(
A
B
C
)
và
A
D
a
,
A
C
2
a
, cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện
A
B
C
D
.
Đọc tiếp
Cho tứ diện A B C D có DA vuông góc với mặt phẳng ( A B C ) và A D = a , A C = 2 a , cạnh BC vuông góc với AB. Tính bán kính r của mặt cầu ngoại tiếp tứ diện A B C D .
![]()
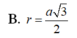
![]()
cho tứ diện ABCD có AB⊥BC ,AB⊥ BD ,AB=a ,BC=2a ,▲ BCD vuông cân tại C có BH⊥AC. Tính góc ( BH,CD)
AB vuông góc BC
AB vuông góc BD
=>AB vuông góc (BCD)
=>AB vuông góc CD
BC vuông góc CD
AB vuông góc CD
=>CD vuông góc (BCA)
=>CD vuông góc BH
=>(BH;CD)=90 độ
Đúng 0
Bình luận (0)
Cho tứ diện ABCD có
B
C
C
D
B
D
2
a
,
A
C
a
2
,
A
B
a
.
Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là A. 90o. B. 60o. C. 45o. D. 30o.
Đọc tiếp
Cho tứ diện ABCD có B C = C D = B D = 2 a , A C = a 2 , A B = a . Góc giữa hai mặt phẳng (ACD) và (BCD) có số đo là
A. 90o.
B. 60o.
C. 45o.
D. 30o.
Cho tứ diện ABCD có AB 2a, tam giác BCD vuông tại C, BD 2a, BC a và
2
A
C
2
-
A
D
2
6
a
2
Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng A.
30
o
B.
90
°
C.
45
o...
Đọc tiếp
Cho tứ diện ABCD có AB = 2a, tam giác BCD vuông tại C, BD = 2a, BC = a và 2 A C 2 - A D 2 = 6 a 2 Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng
A. 30 o
B. 90 °
C. 45 o
D. 60 o
Chọn D
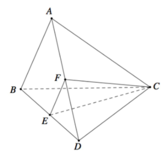
Gọi F là trung điểm cạnh AD có ![]()
Tam giác ∆ E F C có
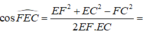
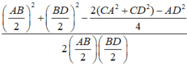
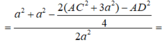
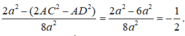
Đúng 0
Bình luận (0)