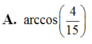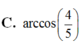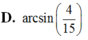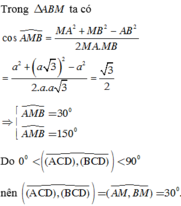Các câu hỏi tương tự
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a,cạnh bên bằng thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằngA. 30o B. 60o C. 45o D. 75o
Đọc tiếp
Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh a,cạnh bên bằng ![]() thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằng
thì góc giữa hai mặt phẳng (A’BC) và (ABC) bằng
A. 30o B. 60o C. 45o D. 75o
Cho tứ diện ABCD có AB AD a
2
, BC BD a và CA CD x. Khoảng cách từ B đến mặt phẳng (ACD) bằng
a
3
2
. Biết thể tích của khối tứ diện bằng
a
3
3
12
. Góc giữa hai mặt phẳng (ACD) và (BCD) là: A.600 B.450 C.900 D.1200
Đọc tiếp
Cho tứ diện ABCD có AB = AD = a 2 , BC = BD = a và CA = CD = x. Khoảng cách từ B đến mặt phẳng (ACD) bằng a 3 2 . Biết thể tích của khối tứ diện bằng a 3 3 12 . Góc giữa hai mặt phẳng (ACD) và (BCD) là:
A.600
B.450
C.900
D.1200
Cho tứ diện có các đỉnh là A(5; 1; 3), B(1; 6; 2), C(5; 0; 4), D(4; 0; 6) Hãy viết phương trình của các mặt phẳng (ACD) và (BCD)
Cho tứ diện ABCD có
A
B
a
;
D
A
B
^
C
B
D
^
;
A
C
a
5
;
A
B
C
^
135
o
. Biết góc giữa hai mặt phẳng (ABD), (BCD) bằng 30o. Thể tích của tứ diện ABCD là...
Đọc tiếp
Cho tứ diện ABCD có A B = a ; D A B ^ = C B D ^ ; A C = a 5 ; A B C ^ = 135 o . Biết góc giữa hai mặt phẳng (ABD), (BCD) bằng 30o. Thể tích của tứ diện ABCD là
A. a 3 2 3
B. a 3 2
C. a 3 3 2
D. a 3 6
Cho tứ diện đều ABCD. Gọi a là góc giữa hai mặt phẳng (ACD) và (BCD). Chọn khẳng định đúng A. a 60
°
B. a 90
°
C. cos a
1
3
D. cos a
2
3
Đọc tiếp
Cho tứ diện đều ABCD. Gọi a là góc giữa hai mặt phẳng (ACD) và (BCD). Chọn khẳng định đúng
A. a = 60 °
B. a = 90 °
C. cos a = 1 3
D. cos a = 2 3
Cho tứ diện ABCD có CDa
2
,
∆
ABC là tam giác đều cạnh a,
∆
ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
Đọc tiếp
Cho tứ diện ABCD có CD=a 2 , ∆ ABC là tam giác đều cạnh a, ∆ ACD vuông tại A. Mặt phẳng (BCD) vuông góc với mặt phẳng (ABD). Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng
![]()
![]()
![]()
![]()
Cho bốn điểm A(-2; 6; 3), B(1; 0; 6), C(0; 2; -1), D(1; 4; 0) Viết phương trình mặt phẳng (BCD). Suy ra ABCD là một tứ diện.
Cho tứ diện ABCD có BD 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD). A. arccos(4/15) B. 1 C. arcsin(4/5) D. arccos(4/5)
Đọc tiếp
Cho tứ diện ABCD có BD = 2, hai tam giác ABD, BCD có diện tích lần lượt là 6 và 10. Biết thể tích của tứ diện ABCD bằng 16, tính số đo góc giữa hai mặt phẳng (ABD) và (BCD).
A. arccos(4/15)
B. 1
C. arcsin(4/5)
D. arccos(4/5)
Cho tứ diện ABCD có BD2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng 16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).
Đọc tiếp
Cho tứ diện ABCD có BD=2. Hai tam giác ABD và BCD có diện tích lần lượt là 6 và 10. Biết thể tích khối tứ diện ABCD bằng 16. Tính số đo góc giữa hai mặt phẳng (ABD), (BCD).